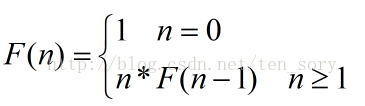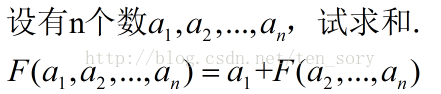遞迴(一)幾個簡單的遞迴例子
剛接觸遞迴的同學,可能難以理解遞迴,難以理解的點可能很多,例如:
1.函式為什麼可以在自己的內部又呼叫自己呢?
2.既然可以自己呼叫自己,那麼遞迴執行過程中一定回有很多層相互巢狀,到底什麼時候不再巢狀呢?
3.遞迴執行過程中,相互巢狀的多層之間會有引數傳遞,多層之間是否會相互影響?
遞迴兩個要素
1.遞迴邊界
2.遞迴的邏輯——遞迴"公式"
遞迴的過程一定有引數的變化,並且引數的變化,和遞迴邊界有關係.
在難度較大的題目中,這兩者均不容易直接得到.
遞迴的種種問題,也許理解的同學可能可以用一句話解釋清楚,但是不理解的同學再怎麼說也沒辦法理解.
下面通過幾個簡單的例子【體會】一下遞迴,先從【感性】的角度理解遞迴.
1.Fibonacci數
我們直到Fibonacci數的遞推公式為:F(0)=F(1)=1,F(n)=F(n-1)+F(n-2) n>=2;
這個明顯地給出了遞迴邊界n=0或1的時候F(n)的值,和遞迴邏輯F(n)=F(n-1)+F(n-2),即遞推公式.所以這個遞迴函式不難書寫
#include<iostream> using namespace std; int F(int n)//函式返回一個數對應的Fibonacci數 { if(n==0 || n==1)//遞迴邊界 return 1; return F(n-1) + F(n-2);//遞迴公式 } int main() { //測試 int n; while(cin >> n) cout << F(n) << endl; return 0; }
2.階乘
階乘的遞迴公式為:
程式碼如下:
#include<iostream>
using namespace std;
int F(int n)
{
if(n==0)//遞迴邊界
return 1;
return n*F(n-1);//遞迴公式
}
int main()
{
int n;
cin >> n;
cout << F(n) << endl;
return 0;
}3.陣列求和
給一個數組a[]:a[0],a[1],...,a[n-1]如何用遞迴的方式求和?
仍然是兩個問題:遞迴邊界和遞迴公式.
遞迴邊界是什麼?一時不容易想到,但是我們想到了求和,多個數的求和過程是什麼,x,y,z,w手動求和的過程是什麼?步驟如下:
x+y=a,任務變為a,z,w求和
a+z=b,任務變為b,w求和
b+w=c得出答案
思考一下,【得出答案】這一步為什麼就可以得出答案呢?(廢話?)是因為,一個數不用相加就能得出答案.
所以,遞迴的邊界就是隻有一個數.
所以,遞迴邊界有了,那麼遞迴公式呢?其實手動計算過程中,隱含了遞迴公式:
其中+為求兩個數的和,F為求多個數的和的遞迴函式.程式碼如下:
#include<iostream>
using namespace std;
int F(int a[],int start,int end)
{
if(start==end)//遞迴邊界
return a[start];
return a[start] + F(a,start+1,end);//遞迴公式
}
int main()
{
int a[] = {1,2,3,4,5};
int s=0,e=4;
cout << F(a,s,e) << endl;
return 0;
}4.求陣列元素最大值
手動求最大值的過程是什麼,遍歷+比較,過程如下:
例如,求3,2,6,7,2,4的最大值:先設定最大值max=-999999,然後將max和陣列元素逐個(遍歷)比較如果a[i]>max,則更新max的值為a[i],否則max不變,繼續向後遍歷,直到遍歷結束.
max<3,則max=3
max>2,max=3不變
max<6,則max=6
max<7,則max=7
max>2,max=7不變
max>4,max=7不變
遍歷結束,max=7為最大值.
和求和類似,遞迴的公式如下:
其中max為求兩個數的較大值函式,F為求多個數的最大值的遞迴函式.程式碼如下:
#include<iostream>
using namespace std;
#define max(a,b) (a>b?a:b)
int F(int a[],int s,int e)
{
if(s==e)
return a[s];
else if(s+1 == e)//遞迴邊界
return max(a[s],a[e]);
return max(a[s],F(a,s+1,e));//遞迴公式!!!
}
int main()
{
int a[] = {5,1,4,6,2};
int s = 0,e = 4;
cout << F(a,s,e) << endl;
return 0;
}之所以,說上面的幾個例子是【簡單例子】,是因為上述所有的遞迴都屬於【單向遞迴】.單向遞迴,遞迴的路徑就是一個方向,所以思路相對比較容易想到.
較難的遞迴問題,一般都不是單向遞迴,而是需要使用【回溯】的方法,遞迴的方法不太容易想到.