SVM是一種典型的兩類分類器，即它只回答屬於正類還是負類的問題。而現實中要解決的問題，往往是多類的問題（少部分例外，例如垃圾郵件過濾，就只需要確定“是”還是“不是”垃圾郵件），比如文字分類，比如數字識別。如何由兩類分類器得到多類分類器，就是一個值得研究的問題。

　　其中一種一勞永逸的方法，就是真的一次性考慮所有樣本，並求解一個多目標函式的優化問題，一次性得到多個分類面。多個超平面把空間劃分為多個區域，每個區域對應一個類別，給一篇文章，看它落在哪個區域就知道了它的分類。

　　看起來很美對不對？只可惜這種演算法還基本停留在紙面上，因為一次性求解的方法計算量實在太大，大到無法實用的地步。

　　稍稍退一步，我們就會想到所謂“一類對其餘”的方法，就是每次仍然解一個兩類分類的問題。比如我們有5個類別，第一次就把類別1的樣本定為正樣本，其餘2，3，4，5的樣本合起來定為負樣本，這樣得到一個兩類分類器，它能夠指出一篇文章是還是不是第1類的；第二次我們把類別2 的樣本定為正樣本，把1，3，4，5的樣本合起來定為負樣本，得到一個分類器，如此下去，我們可以得到5個這樣的兩類分類器（總是和類別的數目一致）。到了有文章需要分類的時候，我們就拿著這篇文章挨個分類器的問：是屬於你的麼？是屬於你的麼？哪個分類器點頭說是了，文章的類別就確定了。這種方法的好處是每個優化問題的規模比較小，而且分類的時候速度很快（只需要呼叫5個分類器就知道了結果）。但有時也會出現兩種很尷尬的情況，例如拿一篇文章問了一圈，每一個分類器都說它是屬於它那一類的，或者每一個分類器都說它不是它那一類的，前者叫分類重疊現象，後者叫不可分類現象。分類重疊倒還好辦，隨便選一個結果都不至於太離譜，或者看看這篇文章到各個超平面的距離，哪個遠就判給哪個。不可分類現象就著實難辦了，只能把它分給第6個類別了……更要命的是，本來各個類別的樣本數目是差不多的，但“其餘”的那一類樣本數總是要數倍於正類（因為它是除正類以外其他類別的樣本之和嘛），這就人為的造成了上一節所說的“資料集偏斜”問題。

　　因此我們還得再退一步，還是解兩類分類問題，還是每次選一個類的樣本作正類樣本，而負類樣本則變成只選一個類（稱為“一對一單挑”的方法，哦，不對，沒有單挑，就是“一對一”的方法，呵呵），這就避免了偏斜。因此過程就是算出這樣一些分類器，第一個只回答“是第1類還是第2類”，第二個只回答“是第1類還是第3類”，第三個只回答“是第1類還是第4類”，如此下去，你也可以馬上得出，這樣的分類器應該有5 X 4/2=10個（通式是，如果有k個類別，則總的兩類分類器數目為k(k-1)/2）。雖然分類器的數目多了，但是在訓練階段（也就是算出這些分類器的分類平面時）所用的總時間卻比“一類對其餘”方法少很多，在真正用來分類的時候，把一篇文章扔給所有分類器，第一個分類器會投票說它是“1”或者“2”，第二個會說它是“1”或者“3”，讓每一個都投上自己的一票，最後統計票數，如果類別“1”得票最多，就判這篇文章屬於第1類。這種方法顯然也會有分類重疊的現象，但不會有不可分類現象，因為總不可能所有類別的票數都是0。看起來夠好麼？其實不然，想想分類一篇文章，我們呼叫了多少個分類器？10個，這還是類別數為5的時候，類別數如果是1000，要呼叫的分類器數目會上升至約500,000個（類別數的平方量級）。這如何是好？

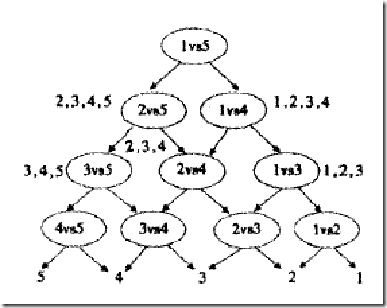
　　看來我們必須再退一步，在分類的時候下功夫，我們還是像一對一方法那樣來訓練，只是在對一篇文章進行分類之前，我們先按照下面圖的樣子來組織分類器（如你所見，這是一個有向無環圖，因此這種方法也叫做DAG SVM）

　　這樣在分類時,我們就可以先問分類器“1對5”（意思是它能夠回答“是第1類還是第5類”），如果它回答5，我們就往左走，再問“2對5”這個分類器，如果它還說是“5”，我們就繼續往左走，這樣一直問下去，就可以得到分類結果。好處在哪？我們其實只調用了4個分類器（如果類別數是k，則只調用k-1個），分類速度飛快，且沒有分類重疊和不可分類現象！缺點在哪？假如最一開始的分類器回答錯誤（明明是類別1的文章，它說成了5），那麼後面的分類器是無論如何也無法糾正它的錯誤的（因為後面的分類器壓根沒有出現“1”這個類別標籤），其實對下面每一層的分類器都存在這種錯誤向下累積的現象。

　　不過不要被DAG方法的錯誤累積嚇倒，錯誤累積在一對其餘和一對一方法中也都存在，DAG方法好於它們的地方就在於，累積的上限，不管是大是小，總是有定論的，有理論證明。而一對其餘和一對一方法中，儘管每一個兩類分類器的泛化誤差限是知道的，但是合起來做多類分類的時候，誤差上界是多少，沒人知道，這意味著準確率低到0也是有可能的，這多讓人鬱悶。
　　而且現在DAG方法根節點的選取（也就是如何選第一個參與分類的分類器），也有一些方法可以改善整體效果，我們總希望根節點少犯錯誤為好，因此參與第一次分類的兩個類別，最好是差別特別特別大，大到以至於不太可能把他們分錯；或者我們就總取在兩類分類中正確率最高的那個分類器作根節點，或者我們讓兩類分類器在分類的時候，不光輸出類別的標籤，還輸出一個類似“置信度”的東東，當它對自己的結果不太自信的時候，我們就不光按照它的輸出走，把它旁邊的那條路也走一走，等等。

大Tips：SVM的計算複雜度
　　使用SVM進行分類的時候，實際上是訓練和分類兩個完全不同的過程，因而討論複雜度就不能一概而論，我們這裡所說的主要是訓練階段的複雜度，即解那個二次規劃問題的複雜度。對這個問題的解，基本上要劃分為兩大塊，解析解和數值解。
　　解析解就是理論上的解，它的形式是表示式，因此它是精確的，一個問題只要有解（無解的問題還跟著摻和什麼呀，哈哈），那它的解析解是一定存在的。當然存在是一回事，能夠解出來，或者可以在可以承受的時間範圍內解出來，就是另一回事了。對SVM來說，求得解析解的時間複雜度最壞可以達到O(Nsv3)，其中Nsv是支援向量的個數，而雖然沒有固定的比例，但支援向量的個數多少也和訓練集的大小有關。
數值解就是可以使用的解，是一個一個的數，往往都是近似解。求數值解的過程非常像窮舉法，從一個數開始，試一試它當解效果怎樣，不滿足一定條件（叫做停機條件，就是滿足這個以後就認為解足夠精確了，不需要繼續算下去了）就試下一個，當然下一個數不是亂選的，也有一定章法可循。有的演算法，每次只嘗試一個數，有的就嘗試多個，而且找下一個數字（或下一組數）的方法也各不相同，停機條件也各不相同，最終得到的解精度也各不相同，可見對求數值解的複雜度的討論不能脫開具體的演算法。
一個具體的演算法，Bunch-Kaufman訓練演算法，典型的時間複雜度在O(Nsv3+LNsv2+dLNsv)和O(dL2)之間，其中Nsv是支援向量的個數，L是訓練集樣本的個數，d是每個樣本的維數（原始的維數，沒有經過向高維空間對映之前的維數）。複雜度會有變化，是因為它不光跟輸入問題的規模有關（不光和樣本的數量，維數有關），也和問題最終的解有關（即支援向量有關），如果支援向量比較少，過程會快很多，如果支援向量很多，接近於樣本的數量，就會產生O(dL2)這個十分糟糕的結果（給10，000個樣本，每個樣本1000維，基本就不用算了，算不出來，呵呵，而這種輸入規模對文字分類來說太正常了）。
　　這樣再回頭看就會明白為什麼一對一方法儘管要訓練的兩類分類器數量多，但總時間實際上比一對其餘方法要少了，因為一對其餘方法每次訓練都考慮了所有樣本（只是每次把不同的部分劃分為正類或者負類而已），自然慢上很多。