【python資料探勘課程】二十一.樸素貝葉斯分類器詳解及中文文字輿情分析
1.樸素貝葉斯數學原理知識
2.naive_bayes用法及簡單案例
3.中文文字資料集預處理
4.樸素貝葉斯中文文字輿情分析
本篇文章為基礎性文章,希望對你有所幫助,如果文章中存在錯誤或不足之處,還請海涵。同時,推薦大家閱讀我以前的文章瞭解基礎知識。
一. 樸素貝葉斯數學原理知識
該基礎知識部分引用文章"機器學習之樸素貝葉斯(NB)分類演算法與Python實現",也強烈推薦大家閱讀博主moxigandashu的文章,寫得很好。同時作者也結合概率論講解,提升下自己較差的
樸素貝葉斯(Naive Bayesian)是基於貝葉斯定理和特徵條件獨立假設的分類方法,它通過特徵計算分類的概率,選取概率大的情況,是基於概率論的一種機器學習分類(監督學習)方法,被廣泛應用於情感分類領域的分類器。
下面簡單回顧下概率論知識:
1.什麼是基於概率論的方法?
通過概率來衡量事件發生的可能性。概率論和統計學是兩個相反的概念,統計學是抽取部分樣本統計來估算總體情況,而概率論是通過總體情況來估計單個事件或部分事情的發生情況。概率論需要已知資料去預測未知的事件。
例如,我們看到天氣烏雲密佈,電閃雷鳴並陣陣狂風,在這樣的天氣特徵(F)下,我們推斷下雨的概率比不下雨的概率大,也就是p(下雨)>p(不下雨),所以認為待會兒會下雨,這個從經驗上看對概率進行判斷。而氣象局通過多年長期積累的資料,經過計算,今天下雨的概率p(下雨)=85%、p(不下雨)=15%,同樣的 p(下雨)>p(不下雨),因此今天的天氣預報肯定預報下雨。這是通過一定的方法計算概率從而對下雨事件進行判斷。

2.條件概率
若Ω是全集,A、B是其中的事件(子集),P表示事件發生的概率,則條件概率表示某個事件發生時另一個事件發生的概率。假設事件B發生後事件A發生的概率為:
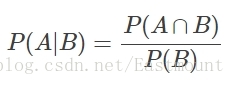
設P(A)>0,則有 P(AB) = P(B|A)P(A) = P(A|B)P(B)。
設A、B、C為事件,且P(AB)>0,則有 P(ABC) = P(A)P(B|A)P(C|AB)。
現在A和B是兩個相互獨立的事件,其相交概率為 P(A∩B) = P(A)P(B)。
3.全概率公式
設Ω為試驗E的樣本空間,A為E的事件,B1、B2、....、Bn為Ω的一個劃分,且P(Bi)>0,其中i=1,2,...,n,則:

P(A) = P(AB1)+P(AB2)+...+P(ABn)
= P(A|B1)P(B1)+P(A|B2)P(B2)+...+P(A|Bn)P(Bn)

全概率公式主要用途在於它可以將一個複雜的概率計算問題,分解為若干個簡單事件的概率計算問題,最後應用概率的可加性求出最終結果。
示例:有一批同一型號的產品,已知其中由一廠生成的佔30%,二廠生成的佔50%,三長生成的佔20%,又知這三個廠的產品次品概率分別為2%、1%、1%,問這批產品中任取一件是次品的概率是多少?
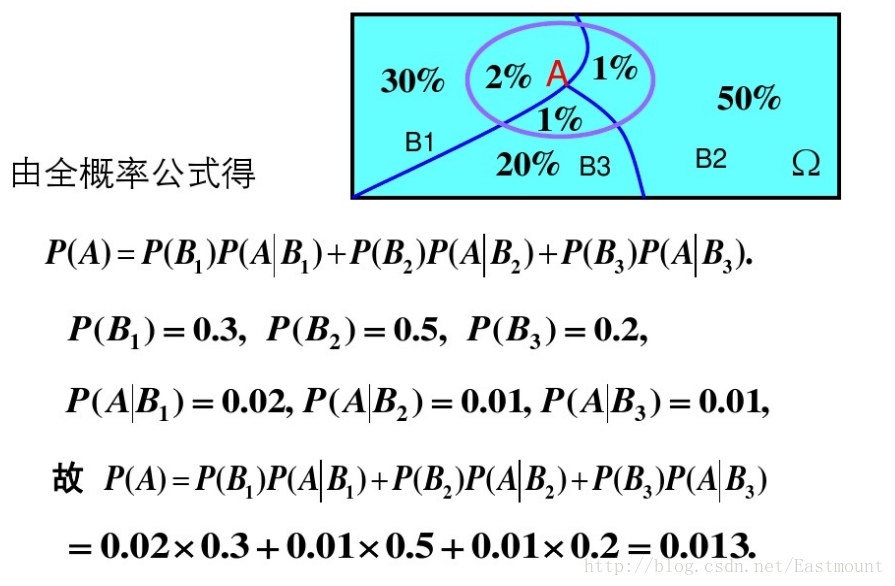
Ω為試驗E的樣本空間,A為E的事件,如果有k個互斥且有窮個事件,即B1、B2、....、Bk為Ω的一個劃分,且P(B1)+P(B2)+...+P(Bk)=1,P(Bi)>0(i=1,2,...,k),則:
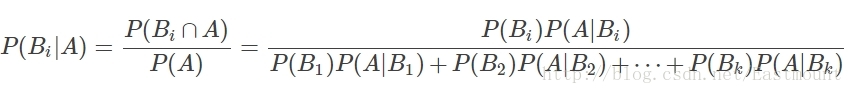
P(A):事件A發生的概率;
P(A∩B):事件A和事件B同時發生的概率;
P(A|B):事件A在時間B發生的條件下發生的概率;
意義:現在已知時間A確實已經發生,若要估計它是由原因Bi所導致的概率,則可用Bayes公式求出。
5.先驗概率和後驗概率
先驗概率是由以往的資料分析得到的概率,泛指一類事物發生的概率,根據歷史資料或主觀判斷未經證實所確定的概率。後驗概率而是在得到資訊之後再重新加以修正的概率,是某個特定條件下一個具體事物發生的概率。

6.樸素貝葉斯分類
貝葉斯分類器通過預測一個物件屬於某個類別的概率,再預測其類別,是基於貝葉斯定理而構成出來的。在處理大規模資料集時,貝葉斯分類器表現出較高的分類準確性。
假設存在兩種分類:
1) 如果p1(x,y)>p2(x,y),那麼分入類別1
2) 如果p1(x,y)<p2(x,y),那麼分入類別2
引入貝葉斯定理即為:
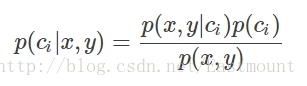
其中,x、y表示特徵變數,ci表示分類,p(ci|x,y)表示在特徵為x,y的情況下分入類別ci的概率,因此,結合條件概率和貝葉斯定理有:
1) 如果p(c1|x,y)>p(c2,|x,y),那麼分類應當屬於類別c1
2) 如果p(c1|x,y)<p(c2,|x,y),那麼分類應當屬於類別c2
貝葉斯定理最大的好處是可以用已知的概率去計算未知的概率,而如果僅僅是為了比較p(ci|x,y)和p(cj|x,y)的大小,只需要已知兩個概率即可,分母相同,比較p(x,y|ci)p(ci)和p(x,y|cj)p(cj)即可。

7.示例講解
假設存在14天的天氣情況和是否能打網球,包括天氣、氣溫、溼度、風等,現在給出新的一天天氣情況,需要判斷我們這一天可以打網球嗎?首先統計出各種天氣情況下打網球的概率,如下圖所示。
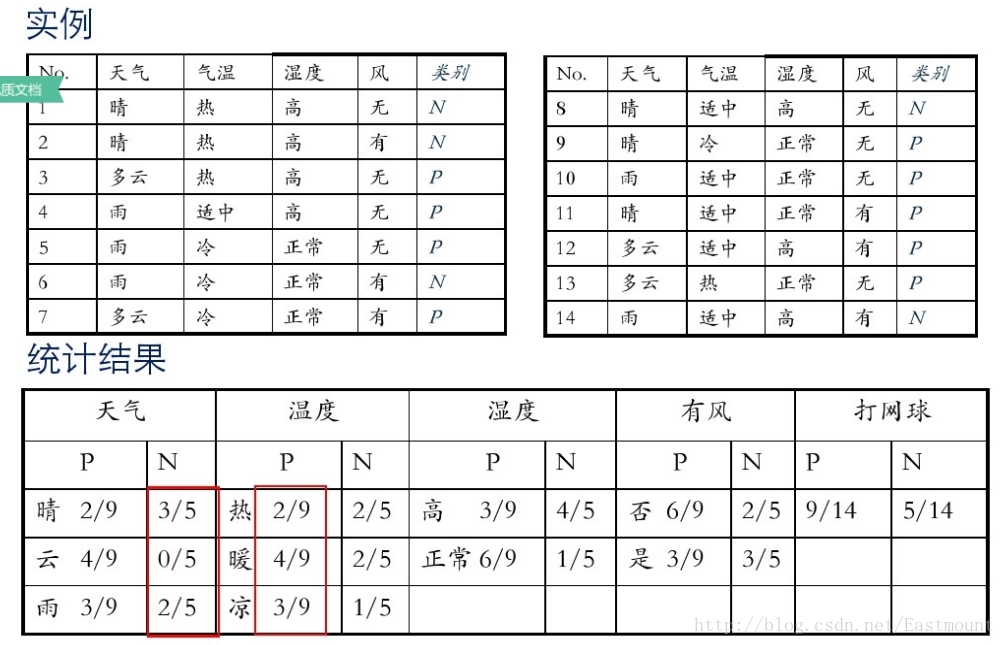
接下來是分析過程,其中包括打網球yse和不打網球no的計算方法。


最後計算結果如下,不去打網球概率為79.5%。

8.優缺點
- 監督學習,需要確定分類的目標
- 對缺失資料不敏感,在資料較少的情況下依然可以使用該方法
- 可以處理多個類別 的分類問題
- 適用於標稱型資料
- 對輸入資料的形勢比較敏感
- 由於用先驗資料去預測分類,因此存在誤差
二. naive_bayes用法及簡單案例
scikit-learn機器學習包提供了3個樸素貝葉斯分類演算法:
- GaussianNB(高斯樸素貝葉斯)
- MultinomialNB(多項式樸素貝葉斯)
- BernoulliNB(伯努利樸素貝葉斯)
1.高斯樸素貝葉斯
呼叫方法為:sklearn.naive_bayes.GaussianNB(priors=None)。
下面隨機生成六個座標點,其中x座標和y座標同為正數時對應類標為2,x座標和y座標同為負數時對應類標為1。通過高斯樸素貝葉斯分類分析的程式碼如下:
# -*- coding: utf-8 -*-
import numpy as np
from sklearn.naive_bayes import GaussianNB
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
Y = np.array([1, 1, 1, 2, 2, 2])
clf = GaussianNB()
clf.fit(X, Y)
pre = clf.predict(X)
print u"資料集預測結果:", pre
print clf.predict([[-0.8, -1]])
clf_pf = GaussianNB()
clf_pf.partial_fit(X, Y, np.unique(Y)) #增加一部分樣本
print clf_pf.predict([[-0.8, -1]])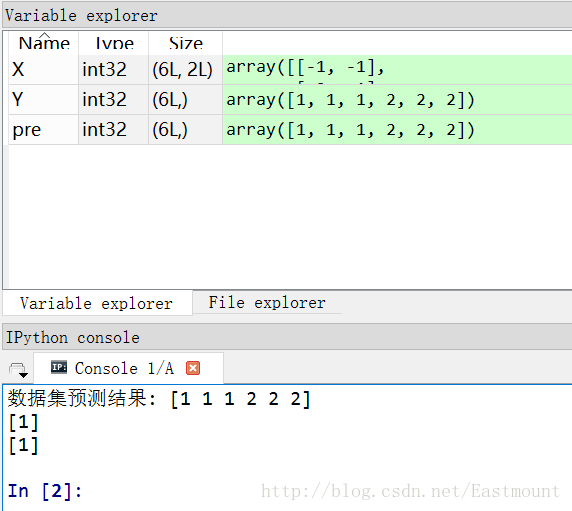
2.多項式樸素貝葉斯
多項式樸素貝葉斯:sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)主要用於離散特徵分類,例如文字分類單詞統計,以出現的次數作為特徵值。
引數說明:alpha為可選項,預設1.0,新增拉普拉修/Lidstone平滑引數;fit_prior預設True,表示是否學習先驗概率,引數為False表示所有類標記具有相同的先驗概率;class_prior類似陣列,陣列大小為(n_classes,),預設None,類先驗概率。
下面是樸素貝葉斯演算法常見的屬性和方法。
1) class_prior_屬性
觀察各類標記對應的先驗概率,主要是class_prior_屬性,返回陣列。程式碼如下:
print clf.class_prior_
#[ 0.5 0.5]2) class_count_屬性
獲取各類標記對應的訓練樣本數,程式碼如下:
print clf.class_count_
#[ 3. 3.]3) theta_屬性
獲取各個類標記在各個特徵上的均值,程式碼如下:
print clf.theta_
#[[-2. -1.33333333]
# [ 2. 1.33333333]]4) sigma_屬性
獲取各個類標記在各個特徵上的方差,程式碼如下:
print clf.theta_
#[[-2. -1.33333333]
# [ 2. 1.33333333]]5) fit(X, y, sample_weight=None)
訓練樣本,X表示特徵向量,y類標記,sample_weight表各樣本權重陣列。
#設定樣本不同的權重
clf.fit(X,Y,np.array([0.05,0.05,0.1,0.1,0.1,0.2,0.2,0.2]))
print clf
print clf.theta_
print clf.sigma_ 輸出結果如下所示:
GaussianNB()
[[-2.25 -1.5 ]
[ 2.25 1.5 ]]
[[ 0.6875 0.25 ]
[ 0.6875 0.25 ]]6) partial_fit(X, y, classes=None, sample_weight=None)
增量式訓練,當訓練資料集資料量非常大,不能一次性全部載入記憶體時,可以將資料集劃分若干份,重複呼叫partial_fit線上學習模型引數,在第一次呼叫partial_fit函式時,必須制定classes引數,在隨後的呼叫可以忽略。
import numpy as np
from sklearn.naive_bayes import GaussianNB
X = np.array([[-1,-1], [-2,-2], [-3,-3], [-4,-4], [-5,-5],
[1,1], [2,2], [3,3]])
y = np.array([1, 1, 1, 1, 1, 2, 2, 2])
clf = GaussianNB()
clf.partial_fit(X,y,classes=[1,2],
sample_weight=np.array([0.05,0.05,0.1,0.1,0.1,0.2,0.2,0.2]))
print clf.class_prior_
print clf.predict([[-6,-6],[4,5],[2,5]])
print clf.predict_proba([[-6,-6],[4,5],[2,5]])輸出結果如下所示:
[ 0.4 0.6]
[1 2 2]
[[ 1.00000000e+00 4.21207358e-40]
[ 1.12585521e-12 1.00000000e+00]
[ 8.73474886e-11 1.00000000e+00]]可以看到點[-6,-6]預測結果為1,[4,5]預測結果為2,[2,5]預測結果為2。同時,predict_proba(X)輸出測試樣本在各個類標記預測概率值。
7) score(X, y, sample_weight=None)
返回測試樣本對映到指定類標記上的得分或準確率。
pre = clf.predict([[-6,-6],[4,5],[2,5]])
print clf.score([[-6,-6],[4,5],[2,5]],pre)
#1.0最後給出一個高斯樸素貝葉斯演算法分析小麥資料集案例,程式碼如下:
# -*- coding: utf-8 -*-
#第一部分 載入資料集
import pandas as pd
X = pd.read_csv("seed_x.csv")
Y = pd.read_csv("seed_y.csv")
print X
print Y
#第二部分 匯入模型
from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()
clf.fit(X, Y)
pre = clf.predict(X)
print u"資料集預測結果:", pre
#第三部分 降維處理
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
newData = pca.fit_transform(X)
print newData[:4]
#第四部分 繪製圖形
import matplotlib.pyplot as plt
L1 = [n[0] for n in newData]
L2 = [n[1] for n in newData]
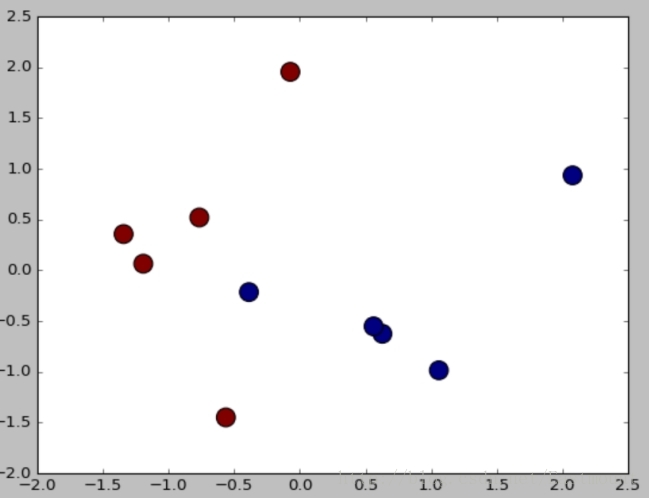
plt.scatter(L1,L2,c=pre,s=200)
plt.show()輸出如下圖所示:

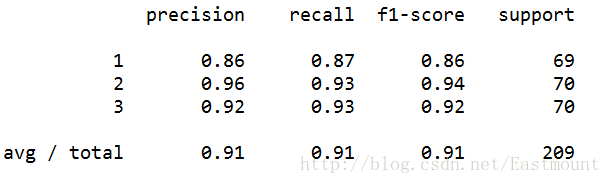
最後對資料集進行評估,主要呼叫sklearn.metrics類中classification_report函式實現的,程式碼如下:
from sklearn.metrics import classification_report
print(classification_report(Y, pre))執行結果如下所示,準確率、召回率和F特徵為91%。
補充下Sklearn機器學習包常用的擴充套件類。
#監督學習
sklearn.neighbors #近鄰演算法
sklearn.svm #支援向量機
sklearn.kernel_ridge #核-嶺迴歸
sklearn.discriminant_analysis #判別分析
sklearn.linear_model #廣義線性模型
sklearn.ensemble #整合學習
sklearn.tree #決策樹
sklearn.naive_bayes #樸素貝葉斯
sklearn.cross_decomposition #交叉分解
sklearn.gaussian_process #高斯過程
sklearn.neural_network #神經網路
sklearn.calibration #概率校準
sklearn.isotonic #保守迴歸
sklearn.feature_selection #特徵選擇
sklearn.multiclass #多類多標籤演算法
#無監督學習
sklearn.decomposition #矩陣因子分解sklearn.cluster # 聚類
sklearn.manifold # 流形學習
sklearn.mixture # 高斯混合模型
sklearn.neural_network # 無監督神經網路
sklearn.covariance # 協方差估計
#資料變換
sklearn.feature_extraction # 特徵提取sklearn.feature_selection # 特徵選擇
sklearn.preprocessing # 預處理
sklearn.random_projection # 隨機投影
sklearn.kernel_approximation # 核逼近三. 中文文字資料集預處理
假設現在需要判斷一封郵件是不是垃圾郵件,其步驟如下:
- 資料集拆分成單詞,中文分詞技術
- 計算句子中總共多少單詞,確定詞向量大小
- 句子中的單詞轉換成向量,BagofWordsVec
- 計算P(Ci),P(Ci|w)=P(w|Ci)P(Ci)/P(w),表示w特徵出現時,該樣本被分為Ci類的條件概率
- 判斷P(w[i]C[0])和P(w[i]C[1])概率大小,兩個集合中概率高的為分類類標
1.資料集讀取
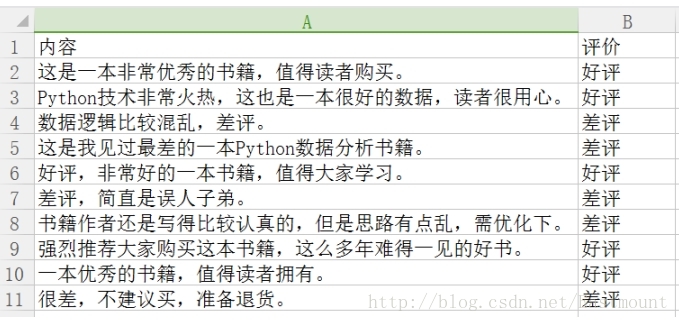
假設存在如下所示10條Python書籍訂單評價資訊,每條評價資訊對應一個結果(好評和差評),如下圖所示:

資料儲存至CSV檔案中,如下圖所示。
下面採用pandas擴充套件包讀取資料集。程式碼如下所示:
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
data = pd.read_csv("data.csv",encoding='gbk')
print data
#取表中的第1列的所有值
print u"獲取第一列內容"
col = data.iloc[:,0]
#取表中所有值
arrs = col.values
for a in arrs:
print a輸出結果如下圖所示,同時可以通過data.iloc[:,0]獲取第一列的內容。

2.中文分詞及過濾停用詞
接下來作者採用jieba工具進行分詞,並定義了停用詞表,即:
stopwords = {}.fromkeys([',', '。', '!', '這', '我', '非常'])
完整程式碼如下所示:
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
import jieba
data = pd.read_csv("data.csv",encoding='gbk')
print data
#取表中的第1列的所有值
print u"獲取第一列內容"
col = data.iloc[:,0]
#取表中所有值
arrs = col.values
#去除停用詞
stopwords = {}.fromkeys([',', '。', '!', '這', '我', '非常'])
print u"\n中文分詞後結果:"
for a in arrs:
#print a
seglist = jieba.cut(a,cut_all=False) #精確模式
final = ''
for seg in seglist:
seg = seg.encode('utf-8')
if seg not in stopwords: #不是停用詞的保留
final += seg
seg_list = jieba.cut(final, cut_all=False)
output = ' '.join(list(seg_list)) #空格拼接
print output然後分詞後的資料如下所示,可以看到標點符號及“這”、“我”等詞已經過濾。

3.詞頻統計
接下來需要將分詞後的語句轉換為向量的形式,這裡使用CountVectorizer實現轉換為詞頻。如果需要轉換為TF-IDF值可以使用TfidfTransformer類。詞頻統計完整程式碼如下所示:
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
import jieba
data = pd.read_csv("data.csv",encoding='gbk')
print data
#取表中的第1列的所有值
print u"獲取第一列內容"
col = data.iloc[:,0]
#取表中所有值
arrs = col.values
#去除停用詞
stopwords = {}.fromkeys([',', '。', '!', '這', '我', '非常'])
print u"\n中文分詞後結果:"
corpus = []
for a in arrs:
#print a
seglist = jieba.cut(a,cut_all=False) #精確模式
final = ''
for seg in seglist:
seg = seg.encode('utf-8')
if seg not in stopwords: #不是停用詞的保留
final += seg
seg_list = jieba.cut(final, cut_all=False)
output = ' '.join(list(seg_list)) #空格拼接
print output
corpus.append(output)
#計算詞頻
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
vectorizer = CountVectorizer() #將文字中的詞語轉換為詞頻矩陣
X = vectorizer.fit_transform(corpus) #計算個詞語出現的次數
word = vectorizer.get_feature_names() #獲取詞袋中所有文字關鍵詞
for w in word: #檢視詞頻結果
print w,
print ''
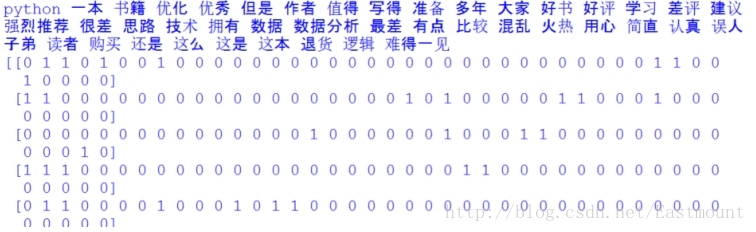
print X.toarray() 輸出結果如下所示,包括特徵詞及對應的10行資料的向量,這就將中文文字資料集轉換為了數學向量的形式,接下來就是對應的資料分析了。
如下所示得到一個詞頻矩陣,每行資料集對應一個分類類標,可以預測新的文件屬於哪一類。

四. 樸素貝葉斯中文文字輿情分析
最後給出樸素貝葉斯分類演算法分析中文文字資料集的完整程式碼。
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
import jieba
#http://blog.csdn.net/eastmount/article/details/50323063
#http://blog.csdn.net/eastmount/article/details/50256163
#http://blog.csdn.net/lsldd/article/details/41542107
####################################
# 第一步 讀取資料及分詞
#
data = pd.read_csv("data.csv",encoding='gbk')
print data
#取表中的第1列的所有值
print u"獲取第一列內容"
col = data.iloc[:,0]
#取表中所有值
arrs = col.values
#去除停用詞
stopwords = {}.fromkeys([',', '。', '!', '這', '我', '非常'])
print u"\n中文分詞後結果:"
corpus = []
for a in arrs:
#print a
seglist = jieba.cut(a,cut_all=False) #精確模式
final = ''
for seg in seglist:
seg = seg.encode('utf-8')
if seg not in stopwords: #不是停用詞的保留
final += seg
seg_list = jieba.cut(final, cut_all=False)
output = ' '.join(list(seg_list)) #空格拼接
print output
corpus.append(output)
####################################
# 第二步 計算詞頻
#
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
vectorizer = CountVectorizer() #將文字中的詞語轉換為詞頻矩陣
X = vectorizer.fit_transform(corpus) #計算個詞語出現的次數
word = vectorizer.get_feature_names() #獲取詞袋中所有文字關鍵詞
for w in word: #檢視詞頻結果
print w,
print ''
print X.toarray()
####################################
# 第三步 資料分析
#
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import classification_report
#使用前8行資料集進行訓練,最後兩行資料集用於預測
print u"\n\n資料分析:"
X = X.toarray()
x_train = X[:8]
x_test = X[8:]
#1表示好評 0表示差評
y_train = [1,1,0,0,1,0,0,1]
y_test = [1,0]
#呼叫MultinomialNB分類器
clf = MultinomialNB().fit(x_train, y_train)
pre = clf.predict(x_test)
print u"預測結果:",pre
print u"真實結果:",y_test
from sklearn.metrics import classification_report
print(classification_report(y_test, pre))輸出結果如下所示,可以看到預測的兩個值都是正確的。即“一本優秀的書籍,值得讀者擁有。”預測結果為好評(類標1),“很差,不建議買,準備退貨。”結果為差評(類標0)。
資料分析:
預測結果: [1 0]
真實結果: [1, 0]
precision recall f1-score support
0 1.00 1.00 1.00 1
1 1.00 1.00 1.00 1
avg / total 1.00 1.00 1.00 2但存在一個問題,由於資料量較小不具備代表性,而真實分析中會使用海量資料進行輿情分析,預測結果肯定頁不是100%的正確,但是需要讓實驗結果儘可能的好。最後補充一段降維繪製圖形的程式碼,如下:
#降維繪製圖形
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
newData = pca.fit_transform(X)
print newData
pre = clf.predict(X)
Y = [1,1,0,0,1,0,0,1,1,0]
import matplotlib.pyplot as plt
L1 = [n[0] for n in newData]
L2 = [n[1] for n in newData]
plt.scatter(L1,L2,c=pre,s=200)
plt.show()輸出結果如圖所示,預測結果和真實結果都是一樣的,即[1,1,0,0,1,0,0,1,1,0]。