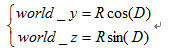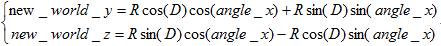背景
當前3D圖形界主要有兩個：微軟的Direct 3D以及某組織的OpenGL。曾經一度OpenGL幾乎佔據所有3D圖形領域，這在巨人微軟面前簡直就是屌絲逆襲。曾幾何時微軟搞IDE borland公式倒閉了，後來微軟搞瀏覽器，網景公司解散，員工捲鋪蓋走人了，也就是說微軟搞誰，誰倒黴。直到OpenGL的出現，打破了這一魔咒，在與微軟競爭的前期，OpenGL幾乎甩了微軟幾條街，併成為事實上的工業標準。後來在微軟的大力絞殺下，OpenGL幾乎被完全趕出了遊戲領域，退居高階圖形領域。基本上現在是微軟的Direct 3D統治遊戲領域，而OpenGL則在高階專業圖形領域佔絕對統治地位。微軟還是微軟，OpenGL已經不是以前的OpenGL了，等會。。等會。。這句話咋這麼熟悉？想起來了趙本山的小品裡說過：你大爺還是你大爺，你大媽已經不是你5年前的大媽了，為什麼這麼說呢？話說搞OpenGL的那家公司被微軟逼瘋了，沒錯。。

座標系空間

在OpenGL裡面，3D座標系的X軸自左向右增大，y軸自下向上增大，z軸正方向從螢幕中心指向觀察者。
座標系有以下幾種：區域性(模型)座標系、世界座標系、相機座標系、螢幕座標系；對應的矩陣變換則有模型變換、檢視(相機)變換、投影變換，其中投影變換分為正視投影、透視投影。而座標系之間的轉換要用到矩陣。世界座標系相當於是虛擬宇宙，位置固定不變，而區域性(模型)座標系是繪圖的一個區域性空間，是相對的，相機座標系是以相機的鏡頭(或者人的眼睛)來觀察物體的視覺空間。在3D中畫圖是現在區域性座標空間繪製，然後通過矩陣變換轉移到世界座標空間，接著轉換到相機空間，然後在投影，最終會在光柵化的二維螢幕上渲染圖形。

區域性座標空間又叫模型空間，繪製圖形是在模型空間繪製，繪製完成後經過模型變換轉換到世界座標系空間。在OpenGL中渲染三維模型是以圖元為最小單位進行渲染的，圖元有三角形，四邊形等，絕大多數情況下都是以三角形圖元渲染。圖元如三角形是有3個頂點組成的，那麼為什麼最小圖元不是頂點而是諸如三角形呢？這就好比提到一個化學物質人們會說這個物質是由很多原子組成的，而不會說是由電子、中子、原子核組成，因為電子、中子及原子核是一個有機整體；同樣三角形圖形的三個頂點也是一個有機整體。

圖一

圖二

我們驚奇的發現這個計算結果正是我們想要的，沒錯，你猜對了，在3D圖形裡面頂點的變換都是通過矩陣完成的，而這個平移變換是最簡單的一種矩陣變換，其他的還有旋轉、縮放等等。上面的圖一、二就是在3D流水線裡經過一些列像上述那樣的矩陣變換最終才從幕後走向臺前展現在大家眼前。由上可以看出每一個頂點經歷了16次乘法運算、12次加法運算，共計28N次計算，當然在矩陣變換之間可能還有進行了諸如光照、紋理等操作。假如一個三維場景共有100萬個頂點，那麼就要做2800萬次計算，這還沒有加上後面的相機變換、投影變換所做的矩陣運算以及光柵化、渲染等操作。由此可以看出來運算量是非常的大。那麼顯示卡能承受如此巨大的運算量嗎？後面會提到，3D 圖形庫(如OpenGL)會在圖形進行渲染前將不必要的頂點裁剪掉，這樣就不用渲染他們了，從而節省了GPU的運算量。但是光是依靠3D 圖形庫的裁剪功能還是不夠，雖然裁剪掉了不需進行渲染的頂點，然而這些頂點已經消耗掉了大量的矩陣運算，尤其是當場景非常細膩的時候也就意味著頂點數目非常巨大。那麼有沒有方法可以在座標系統進行矩陣變換前就被提前裁剪掉呢？答案是肯定的。舉個例子，對於圖一中的地形網格來說，他被渲染到螢幕是有條件的，其一：不在照相機視景體空間內的物體將被忽略不予處理；其二：對於遠處的地面以低解析度渲染，近處則以高解析度渲染；其三：粗糙的部分以高解析度渲染，平坦的部分以低解析度渲染。假如有一個600X600的網格經過測試不在照相機的視景體內，那麼這36萬個頂點就不用進行後續的大量矩陣運算，而測試所消耗是由8個頂點組成的六面體，這個運算量的消耗無疑是值得的。至於如何進行相機裁剪，在層次細節演算法裡面將會詳細說明。在OpenGL以及D3D裡面使用者一般不會直接操作矩陣，OpenGL會將使用者的函式呼叫解釋為矩陣，比如使用者呼叫gluPerspective(引數。。)時，OpenGL會根據函式的引數設定檢視矩陣並與當前的檢視矩陣相乘。

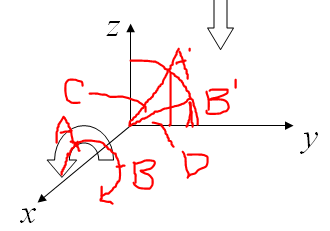
世界座標系空間經過上面的平移操作物體就被移動到世界座標系，這個座標系是固定不變的，相當於虛擬宇宙中心。此時物體還不能呈現於螢幕，還要經歷九九八十一難才能與觀眾見面。進入世界座標系以後，照相機的視點可能不在原點，並且視點可能還不是朝向z軸負方向。此時就要將照相機平移到世界座標系原點，並且調整方向使相機視點朝向z軸負方向。之所以要這樣調整是因為如果相機位於原點並朝向z軸負方向的話會給處理帶來極大的方便，至於是什麼方便呢，我也不知道，反正是專家說的，至於你信不信，反正我是信了。在說明如何變換到相機空間我們先來看一下幾個矩陣操作。設有世界座標系空間的某一個點A(world_x,world_y,world_z)分別繞x軸 y軸 z軸旋轉angle_x、angle_y、angle_z度到達B點。那麼求其旋轉後的座標。

圖三

這裡為了更好推導將座標系進行了旋轉。

如圖三A點繞x軸 旋轉angle_x度求其旋轉後的座標。A點繞X軸旋轉所形成的平面必定與y軸 z軸所構成的平面平行，因此將A點 B點投射到y_z平面上得到A撇點 B撇點，A撇  B撇點在z y平面上的座標顯而易見就是A點 B點對應的 y z座標。如圖可知C角的大小就是angle_x 即C=angle_x;D點對應的那個角是OA與y軸的夾角。

對於B撇點:

對於A撇點：

將第一個方程式展開得到:

將第二個方程代入第三個方程式得到：

(world_x, world_y*cos(angle_x)+world_z*sin(angle_x),-world_y*sin(angle_x)+world_z*cos(angle_x));
下面我們再看一個矩陣運算：

矩陣一

我們再一次吃驚的發現這個正是我們所想要的結果，難道冥冥之中矩陣與3D圖形變換有著不解之緣？OpenGL裡面矩陣是按照列優先的原則儲存於一個一維數組裡面，三維頂點不是以三維向量二是以四維向量來表示比如(x,y,z,w)來表示的，w初始預設情況下為1，在變換過程中w的值會跟著發生變化，並且w也有它的用處，此是後話。我們來看一個更加一般的矩陣：

在上述的矩陣變換中我們曾經說過繞X軸旋轉物體angle_x度，這相當於物體不動把座標軸繞X軸向相反的方向旋轉angle_x度。如圖A表示繞X軸旋轉的角度，如果以上述變換為例，那麼A=angle_x。顯然在新的區域性座標系下對應的B C點在原來的座標系中的座標分別是
(0,-1*sin(angle_x),1*cos(angle_x))           (0,1*cos(angle_x),1*sin(angle_x)) 再看矩陣一，發現這個正是新的座標系的三個方向向量，這個方向向量是以原座標系為參考系得來的。在3D中我們旋轉物體與物體不動旋轉座標系的效果是一樣的，只是四維方式的問題而已。在回過頭來看矩陣二，我們發現(translate_x ,translate_y,translate_z)是區域性矩陣的原點在原座標系下的座標，而(x1,y1,z1)是新的區域性座標系的x軸上的一個點在原座標系下的座標，其他的以此類推，區域性座標系的原點定了，三個座標軸上的點也定了，我們吃驚的發現區域性座標系在原座標系為參考的情況下已經描繪出來了。如果。。如果原座標系是世界座標系，沒錯，如果成真的話我們就經過一系列矩陣變換得到了區域性座標系在世界座標系中的位置，於是就刻畫出來了三維物體的頂點座標在世界座標系下的座標值。
現在還記得我們一開始的問題嗎？你可能已經不記得了，問題是如何將世界座標系變換到相機座標系。

圖片來自3D遊戲程式設計大師。

如上圖相機位置(cam_x,cam_y,cam_z)與y軸夾角為angle_y。如果要變換到相機空間的話首先要將相機平移到原點，結合前面所說的也就是設定矩陣的最後一列translate_x=-cam_x, translate_y=-cam_y, translate_z=-cam_z，然後使相機的鏡頭繞y軸旋轉-angle_y度。前面已經講過繞X軸旋轉angle_x度的矩陣方程，那麼繞x軸旋轉-angle_x度的方法就是將前述矩陣的角度設定為-angle_x就行了，y軸旋轉的也可以以此類推。

相機座標空間經過上述的矩陣變換已經到達了相機座標空間，現在到了投影的時刻了，前面定義了相機的位置和方向，但是相機的視野不是無限遠的，必須為它制定一個視景體，在視景體內的物體將被投影到視平面，不在視景體內的物體將被丟棄不處理

如圖便是一個視景體，這個投影是透視投影，所謂透視投影就是給人一中置身於實際場景中的感覺，遠處的物體顯得小，近處的物體顯得大。還有一中投影叫正視投影，這個主要用於CAD程式中。三維圖形主要使用透視投影。在OpenGL這個視景體可以用api函式gluPerspective(angle,fov,w_div_h,near,far)來定義。這個函式將產生一個透視投影矩陣並與當前的投影矩陣相乘。

投影空間經過上述矩陣變換就到了投影空間了，接著就是後續的視口變換，渲染等工作了。

裁剪現在我們再來看一個地形網格

圖片三

這個地形網格和圖片一是一個程式生成的，不同的是前者調節係數是8，後者調節係數是25結果導致了後者的解析度明顯大於前者。經過前面座標系空間變換的介紹我們知道這幅地形網格呈現在我們眼前之前經歷了模型變換，檢視變換，投影變換等。這個地形網格是513*513尺寸，而且沒有達到完全解析度，那麼如果達到了完全解析度，勢必頂點數目大幅增加，再如 如果地形尺寸是10000*10000呢，頂點數將增加400倍，再如一個實際的場景可能還有大量的樹木，房屋，動物，人車等。除了矩陣運算還有紋理貼圖，光照，霧化等，處理起來相當的消耗GPU和CPU。如果不控制好的話，系統渲染後執行非常卡。其中有一個可以改善的方法是LOD演算法即層次細節演算法，這個演算法常用來繪製大規模實時地形。這個演算法其中需要用到一個叫相機裁剪的演算法。接下來就說一下相機裁剪。所謂相機裁剪就是在上圖視景體中的物體進行處理，不在裡面的物體被丟棄。前面已經說過渲染的時候OpenGL會自動丟棄不在視景體內的物體以避免渲染，而此處的裁剪進一步減少了矩陣運算的次數，也就是說如果物體需要裁剪的話，那麼在模型空間就被裁剪了，而沒有經過後續的各種矩陣變換。那麼必須設計一個演算法來檢測某個物體是否被相機裁剪。方法之一是將待處理的物體構造一個AABB包圍盒，然後用包圍盒的頂點與物體頂點所在的平面做相交測試，不想交就被裁剪掉，否則保留。

typedef struc aabb
{    
      someType  min[3];
      someType  max[3]; 
} AABB;

這個結構體裡面min[3]裡面儲存的是(min_x,min_y,min_z)對應max[3]裡面儲存(max_x,max_y,max_z) 這些座標是採用某種方法找到的物體的最小座標或最大座標值，最笨最耗時的辦法就是遍歷物體的每個頂點找到對應的最小最大座標值

那麼怎麼求視景體的六個面的方程呢？在OpenGL中經過透視投影后前文的視景體變為了規則的長方體，這個投影空間中頂點的座標形式為(pro_x,pro_y,pro_z,w)，現在到了w值大顯神通的時候了，如果程式設計師沒有在程式中故意操作矩陣的值，那麼現在這個w就是每個座標值得各個分量的絕對值的最大範圍，顯而易見如果物體的座標滿足-w<x<w;-w<y<w;-w<z<w的話那麼物體在這個投影空間內否則被裁減掉。這個投影空間的左平面的方程為x=-w,但是我們把它寫作-x-w=0的形式，這樣他的法向量就是(-1,0,0)也就是指向投影空間的外部，保證其他六個面的法向量也指向物體外部，這樣是為了方便後面的相交測試，當然使所有平面方程的法向量指向空間內部也是可以的，總之保持一致性就可以了。對於一個普通的平面方程A*x+B*y+C*z+D=0和一個頂點(a,b,c)將其代入原方程，如果A*a+B*b+C*c+D=0的話這個頂點就在平面上，若小於零則在平面一側若大於零則在另一側，這個方法就可以用於包圍盒與相機裁剪測試中。我們的目的是在物體經不經過模型、檢視、投影變換直接進行相交測試，那麼必然要求得相機視景體在經過相機變換 模型變換前的六面體的6個平面方程。那麼從當前的這個投影后的長方體就可以推匯出這個所需要的六面體的六個面的方程。設區域性座標系下物體的任意一個頂點是vertex_local=(local_x,local_y,local_z,w)這裡w=1;經過投影變換後的座標vertex_per=(per_x,per_y,per_z);設M是模型變換矩陣，V是相機變換矩陣，P是透視投影變換矩陣。那麼將會有如下的座標變換關係vertex_local*MVP=vertex_per；其中MVP是模型檢視投影三個矩陣的乘積，這個是顯而易見的。這是目前可以利用的一個等式，我們就是從這個等式推匯出面的方程。這其中的矩陣M V P分別是模型 檢視 投影矩陣，可以由OpenGL api獲得，然後計算其乘積就行了。先來看一個圖片：

在這個矩陣乘法當中一個原始座標乘以一個4*4矩陣得到一個新的座標。
其中 x_new=X1*x_origin+x2*y_origin+x3*z_origin+x_t*w;
    w_new= a*x_origin+b*y_origin+c*z_origin+d*w;
由上述可知投影之後在x軸方向的範圍是[-w_new,w_new]
所以右平面上的點的方程式x_new=w_new;
結合上兩個方程式得到：x_origin*(X1-a)+y_origin*(X2-b) +z_origin*(X3-c)+w*(x_t-d)=0;
由於初始w=1;所以     x_origin*(X1-a)+y_origin*(X2-b) +z_origin*(X3-c)+(x_t-d)=0;
其中小括號裡的資料是可以計算出來的，相當於常量，於是上式的形式就是Ax+By+Cz+D=0。顯然這是個平面的方程，而x y z是初始的點，那麼這個方程就是初始的點所在的平面的方程。同樣道理求得另外5個面的方程，然後做相交測試，便可以進行裁剪了。現在包圍盒aabb 六個平面的方程已經了。
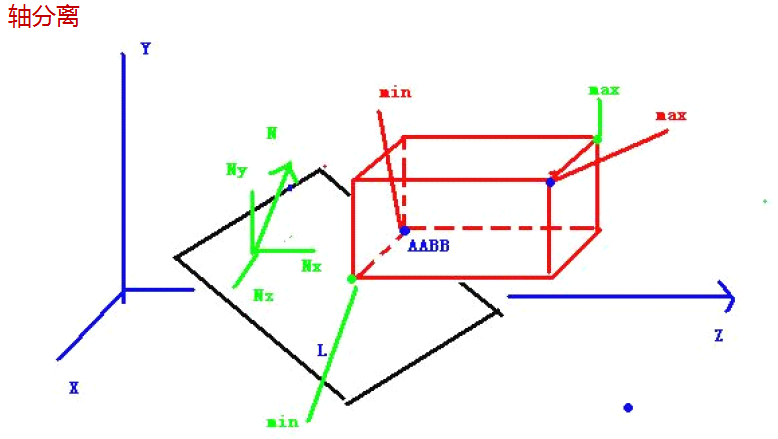
那麼現在如何進行相交測試呢？

如圖一開始最小 最大點是紅色的min max點，經過軸分離後最小 最大點變化為綠色的min  max在知道包圍盒aabb和6個平面的方程後就可以使用軸分離方向來測試相交問題。如果aabb最小的點在某個平面外的話，那麼其他點一定在平面外。但是現在有一個問題就是怎麼定義最大最小點，最大最小分別表示距離平面距離最大最小的點。一開始沒有考慮平面的時候直接比較座標值的大小來確定最大最小點，現在引入平面方程後就要重新調整aabb得到新的包圍盒。這裡不試圖給出嚴格的數學證明，只舉一個簡單的例子來說明為何要重新調整aabb。軸分離的話就是分別考慮x y z軸。現在假設考慮x軸，上述的投影后的長方體左平面方程為-x-w=0；假設aabb.max[]={-3,-3,-3} aabb.min[]={-5,-5,-5}但是現在距離-x-w=0(w<1.0) 最小的點顯然是{-3,-5,-5) 最大點顯然應該是(-5,-3,-3)，然後y z軸以此類推，得到更新後的aabb。將新的aabb.min代入上面的平面方程如果大於0的話，演算法立刻return，這個aabb不在視鏡體內，如果小於0的話，在將aabb.max代入，如果大於0的話設定標誌insect=true;然後迴圈處理另外幾個平面方程。最終若aabb不在包圍盒內將會在迴圈的過程中return，如果迴圈順利結束，並且insect=true,說明aabb與視景體相交，否則aabb完全在視景體中。

自此，本文就結束了，這只是任務中的一個小部分。。還有很多其他任務需要做。。