[摘要]：本文提出了一種完全通過點對點技術實現的電子現金系統，它使得線上支付能夠直接由一方發起並支付給另外一方，中間不需要通過任何的金融機構。雖然數字簽名（Digital signatures）部分解決了這個問題，但是如果仍然需要第三方的支援才能防止雙重支付（double-spending）的話，那麼這種系統也就失去了存在的價值。我們(we)在此提出一種解決方案，使現金系統在點對點的環境下執行，並防止雙重支付問題。該網路通過隨機雜湊（hashing）對全部交易加上時間戳（timestamps），將它們合併入一個不斷延伸的基於隨機雜湊的工作量證明（proof-of-work）的鏈條作為交易記錄，除非重新完成全部的工作量證明，形成的交易記錄將不可更改。最長的鏈條不僅將作為被觀察到的事件序列（sequence）的證明，而且被看做是來自CPU計算能力最大的池（pool）。只要大多數的CPU計算能力都沒有打算合作起來對全網進行攻擊，那麼誠實的節點將會生成最長的、超過攻擊者的鏈條。這個系統本身需要的基礎設施非常少。資訊盡最大努力在全網傳播即可，節點(nodes)可以隨時離開和重新加入網路，並將最長的工作量證明鏈條作為在該節點離線期間發生的交易的證明。

1. 簡介

網際網路上的貿易，幾乎都需要藉助金融機構作為可資信賴的第三方來處理電子支付資訊。雖然這類系統在絕大多數情況下都運作良好，但是這類系統仍然內生性地受制於“基於信用的模式”(trust based model)的弱點。我們無法實現完全不可逆的交易，因為金融機構總是不可避免地會出面協調爭端。而金融中介的存在，也會增加交易的成本，並且限制了實際可行的最小交易規模，也限制了日常的小額支付交易。並且潛在的損失還在於，很多商品和服務本身是無法退貨的，如果缺乏不可逆的支付手段，網際網路的貿易就大大受限。因為有潛在的退款的可能，就需要交易雙方擁有信任。而商家也必須提防自己的客戶，因此會向客戶索取完全不必要的個人資訊。而實際的商業行為中，一定比例的欺詐性客戶也被認為是不可避免的，相關損失視作銷售費用處理。而在使用物理現金的情況下，這些銷售費用和支付問題上的不確定性卻是可以避免的，因為此時沒有第三方信用中介的存在。
所以，我們非常需要這樣一種電子支付系統，它基於密碼學原理而不基於信用，使得任何達成一致的雙方，能夠直接進行支付，從而不需要第三方中介的參與。杜絕回滾(reverse)支付交易的可能，這就可以保護特定的賣家免於欺詐；而對於想要保護買家的人來說，在此環境下設立通常的第三方擔保機制也可謂輕鬆加愉快。在這篇論文中，我們(we)將提出一種通過點對點分散式的時間戳伺服器來生成依照時間前後排列並加以記錄的電子交易證明，從而解決雙重支付問題。只要誠實的節點所控制的計算能力的總和，大於有合作關係的(cooperating)攻擊者的計算能力的總和，該系統就是安全的。

2. 交易(Transactions)

我們定義，一枚電子貨幣（an electronic coin）是這樣的一串數字簽名：每一位所有者通過對前一次交易和下一位擁有者的公鑰(Public key) 簽署一個隨機雜湊的數字簽名，並將這個簽名附加在這枚電子貨幣的末尾，電子貨幣就傳送給了下一位所有者。而收款人通過對簽名進行檢驗，就能夠驗證該鏈條的所有者。

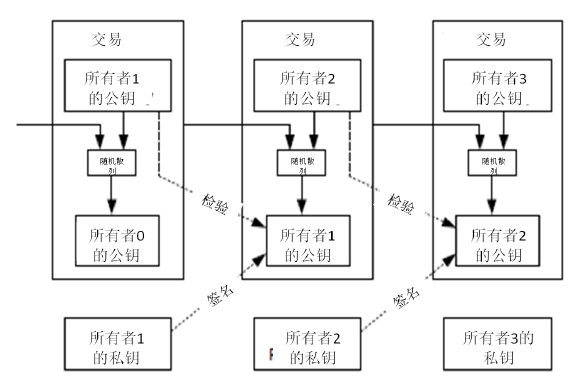
該過程的問題在於，收款人將難以檢驗，之前的某位所有者，是否對這枚電子貨幣進行了雙重支付。通常的解決方案，就是引入信得過的第三方權威，或者類似於造幣廠(mint)的機構，來對每一筆交易進行檢驗，以防止雙重支付。在每一筆交易結束後，這枚電子貨幣就要被造幣廠回收，而造幣廠將發行一枚新的電子貨幣；而只有造幣廠直接發行的電子貨幣，才算作有效，這樣就能夠防止雙重支付。可是該解決方案的問題在於，整個貨幣系統的命運完全依賴於運作造幣廠的公司，因為每一筆交易都要經過該造幣廠的確認，而該造幣廠就好比是一家銀行。
我們需要收款人有某種方法，能夠確保之前的所有者沒有對更早發生的交易實施簽名。從邏輯上看，為了達到目的，實際上我們需要關注的只是於本交易之前發生的交易，而不需要關注這筆交易發生之後是否會有雙重支付的嘗試。為了確保某一次交易是不存在的，那麼唯一的方法就是獲悉之前發生過的所有交易。在造幣廠模型裡面，造幣廠獲悉所有的交易，並且決定了交易完成的先後順序。如果想要在電子系統中排除第三方中介機構，那麼交易資訊就應當被公開宣佈（publicly announced）[1] ，我們需要整個系統內的所有參與者，都有唯一公認的歷史交易序列。收款人需要確保在交易期間絕大多數的節點都認同該交易是首次出現。

3. 時間戳伺服器(Timestamp server)

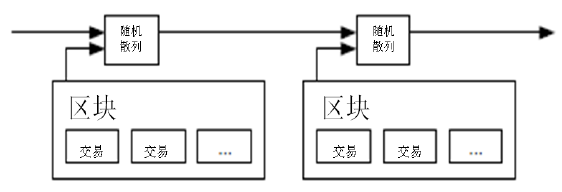
本解決方案首先提出一個“時間戳伺服器”。時間戳伺服器通過對以區塊(block)形式存在的一組資料實施隨機雜湊而加上時間戳，並將該隨機雜湊進行廣播，就像在新聞或世界性新聞組網路（Usenet）的發帖一樣[2][3][4][5] 。顯然，該時間戳能夠證實特定資料必然於某特定時間是的確存在的，因為只有在該時刻存在了才能獲取相應的隨機雜湊值。每個時間戳應當將前一個時間戳納入其隨機雜湊值中，每一個隨後的時間戳都對之前的一個時間戳進行增強(reinforcing)，這樣就形成了一個鏈條（Chain）。

4. 工作量證明（Proof-of-Work）

為了在點對點的基礎上構建一組分散化的時間戳伺服器，僅僅像報紙或世界性新聞網路組一樣工作是不夠的，我們還需要一個類似於亞當•柏克（Adam Back）提出的雜湊現金（Hashcash）[6] 。在進行隨機雜湊運算時，工作量證明機制引入了對某一個特定值的掃描工作，比方說SHA-256下，隨機雜湊值以一個或多個0開始。那麼隨著0的數目的上升, 找到這個解所需要的工作量將呈指數增長，而對結果進行檢驗則僅需要一次隨機雜湊運算。
我們在區塊中補增一個隨機數(Nonce)，這個隨機數要使得該給定區塊的隨機雜湊值出現了所需的那麼多個0。我們通過反覆嘗試來找到這個隨機數，直到找到為止，這樣我們就構建了一個工作量證明機制。只要該CPU耗費的工作量能夠滿足該工作量證明機制，那麼除非重新完成相當的工作量，該區塊的資訊就不可更改。由於之後的區塊是連結在該區塊之後的，所以想要更改該區塊中的資訊，就還需要重新完成之後所有區塊的全部工作量。

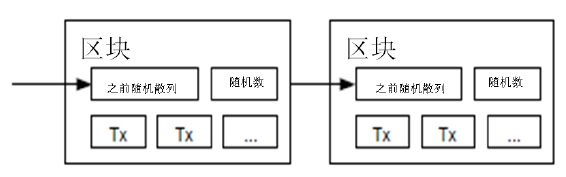
同時，該工作量證明機制還解決了在集體投票表決時，誰是大多數的問題。如果決定大多數的方式是基於IP地址的，一IP地址一票，那麼如果有人擁有分配大量IP地址的權力，則該機制就被破壞了。而工作量證明機制的本質則是一CPU一票。“大多數”的決定表達為最長的鏈，因為最長的鏈包含了最大的工作量。如果大多數的CPU為誠實的節點控制，那麼誠實的鏈條將以最快的速度延長，並超越其他的競爭鏈條。如果想要對業已出現的區塊進行修改，攻擊者必須重新完成該區塊的工作量外加該區塊之後所有區塊的工作量，並最終趕上和超越誠實節點的工作量。我們將在後文證明，設想一個較慢的攻擊者試圖趕上隨後的區塊，那麼其成功概率將呈指數化遞減。
另一個問題是，硬體的運算速度在高速增長，而節點參與網路的程度則會有所起伏。為了解決這個問題，工作量證明的難度(the proof-of-work difficulty)將採用移動平均目標的方法來確定，即令難度指向令每小時生成區塊的速度為某一個預定的平均數。如果區塊生成的速度過快，那麼難度就會提高。

5. 網路

執行該網路的步驟如下：
1) 新的交易向全網進行廣播；
2) 每一個節點都將收到的交易資訊納入一個區塊中；
3) 每個節點都嘗試在自己的區塊中找到一個具有足夠難度的工作量證明；
4) 當一個節點找到了一個工作量證明，它就向全網進行廣播；
5) 當且僅當包含在該區塊中的所有交易都是有效的且之前未存在過的，其他節點才認同該區塊的有效性；
6) 其他節點表示他們接受該區塊，而表示接受的方法，則是在跟隨該區塊的末尾，製造新的區塊以延長該鏈條，而將被接受區塊的隨機雜湊值視為先於新區快的隨機雜湊值。
節點始終都將最長的鏈條視為正確的鏈條，並持續工作和延長它。如果有兩個節點同時廣播不同版本的新區塊，那麼其他節點在接收到該區塊的時間上將存在先後差別。當此情形，他們將在率先收到的區塊基礎上進行工作，但也會保留另外一個鏈條，以防後者變成最長的鏈條。該僵局（tie）的打破要等到下一個工作量證明被發現，而其中的一條鏈條被證實為是較長的一條，那麼在另一條分支鏈條上工作的節點將轉換陣營，開始在較長的鏈條上工作。
所謂“新的交易要廣播”，實際上不需要抵達全部的節點。只要交易資訊能夠抵達足夠多的節點，那麼他們將很快被整合進一個區塊中。而區塊的廣播對被丟棄的資訊是具有容錯能力的。如果一個節點沒有收到某特定區塊，那麼該節點將會發現自己缺失了某個區塊，也就可以提出自己下載該區塊的請求。

6. 激勵

我們約定如此：每個區塊的第一筆交易進行特殊化處理，該交易產生一枚由該區塊創造者擁有的新的電子貨幣。這樣就增加了節點支援該網路的激勵，並在沒有中央集權機構發行貨幣的情況下，提供了一種將電子貨幣分配到流通領域的一種方法。這種將一定數量新貨幣持續增添到貨幣系統中的方法，非常類似於耗費資源去挖掘金礦並將黃金注入到流通領域。此時，CPU的時間和電力消耗就是消耗的資源。
另外一個激勵的來源則是交易費（transaction fees）。如果某筆交易的輸出值小於輸入值，那麼差額就是交易費，該交易費將被增加到該區塊的激勵中。只要既定數量的電子貨幣已經進入流通，那麼激勵機制就可以逐漸轉換為完全依靠交易費，那麼本貨幣系統就能夠免於通貨膨脹。
激勵系統也有助於鼓勵節點保持誠實。如果有一個貪婪的攻擊者能夠調集比所有誠實節點加起來還要多的CPU計算力，那麼他就面臨一個選擇：要麼將其用於誠實工作產生新的電子貨幣，或者將其用於進行二次支付攻擊。那麼他就會發現，按照規則行事、誠實工作是更有利可圖的。因為該等規則使得他能夠擁有更多的電子貨幣，而不是破壞這個系統使得其自身財富的有效性受損。

7. 回收硬碟空間

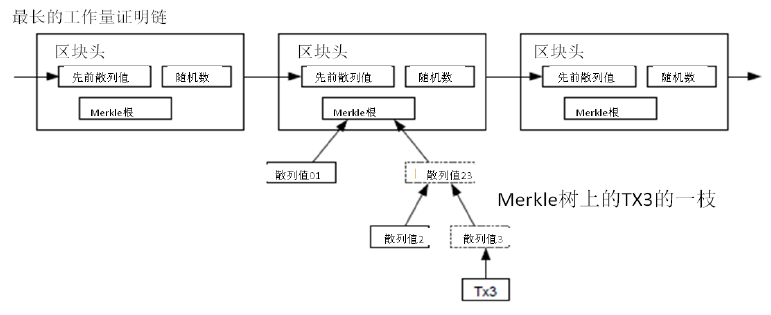
如果最近的交易已經被納入了足夠多的區塊之中，那麼就可以丟棄該交易之前的資料，以回收硬碟空間。為了同時確保不損害區塊的隨機雜湊值，交易資訊被隨機雜湊時，被構建成一種Merkle樹（Merkle tree）[7] 的形態，使得只有根(root)被納入了區塊的隨機雜湊值。通過將該樹（tree）的分支拔除（stubbing）的方法，老區塊就能被壓縮。而內部的隨機雜湊值是不必儲存的。

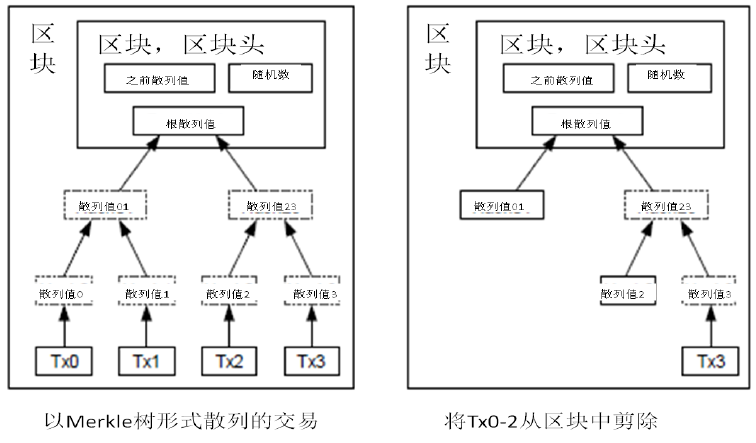
不含交易資訊的區塊頭（Block header）大小僅有80位元組。如果我們設定區塊生成的速率為每10分鐘一個，那麼每一年產生的資料位4.2MB。（80 bytes * 6 * 24 * 365 = 4.2MB）。2008年，PC系統通常的記憶體容量為2GB，按照摩爾定律的預言，即使將全部的區塊頭儲存於記憶體之中都不是問題。

8. 簡化的支付確認（Simplified Payment Verification）

在不執行完整網路節點的情況下，也能夠對支付進行檢驗。一個使用者需要保留最長的工作量證明鏈條的區塊頭的拷貝，它可以不斷向網路發起詢問，直到它確信自己擁有最長的鏈條，並能夠通過merkle的分支通向它被加上時間戳並納入區塊的那次交易。節點想要自行檢驗該交易的有效性原本是不可能的，但通過追溯到鏈條的某個位置，它就能看到某個節點曾經接受過它，並且於其後追加的區塊也進一步證明全網曾經接受了它。

當此情形，只要誠實的節點控制了網路，檢驗機制就是可靠的。但是，當全網被一個計算力佔優的攻擊者攻擊時，將變得較為脆弱。因為網路節點能夠自行確認交易的有效性，只要攻擊者能夠持續地保持計算力優勢，簡化的機制會被攻擊者焊接的（fabricated）交易欺騙。那麼一個可行的策略就是，只要他們發現了一個無效的區塊，就立刻發出警報，收到警報的使用者將立刻開始下載被警告有問題的區塊或交易的完整資訊，以便對資訊的不一致進行判定。對於日常會發生大量收付的商業機構，可能仍會希望執行他們自己的完整節點，以保持較大的獨立完全性和檢驗的快速性。

9. 價值的組合與分割（Combining and Splitting Value）

雖然可以單個單個地對電子貨幣進行處理，但是對於每一枚電子貨幣單獨發起一次交易將是一種笨拙的辦法。為了使得價值易於組合與分割，交易被設計為可以納入多個輸入和輸出。一般而言是某次價值較大的前次交易構成的單一輸入，或者由某幾個價值較小的前次交易共同構成的並行輸入，但是輸出最多隻有兩個：一個用於支付，另一個用於找零（如有）。
需要指出的是，當一筆交易依賴於之前的多筆交易時，這些交易又各自依賴於多筆交易，但這並不存在任何問題。因為這個工作機制並不需要展開檢驗之前發生的所有交易歷史。

10. 隱私（Privacy）

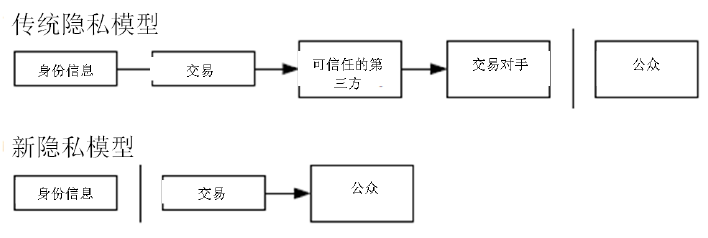
傳統的造幣廠模型為交易的參與者提供了一定程度的隱私保護，因為試圖向可信任的第三方索取交易資訊是嚴格受限的。但是如果將交易資訊向全網進行廣播，就意味著這樣的方法失效了。但是隱私依然可以得到保護：將公鑰保持為匿名。公眾得知的資訊僅僅是有某個人將一定數量的貨幣發所給了另外一個人，但是難以將該交易同特定的人聯絡在一起，也就是說，公眾難以確信，這些人究竟是誰。這同股票交易所釋出的資訊是類似的，股票交易發生的時間、交易量是記錄在案且可供查詢的，但是交易雙方的身份資訊卻不予透露。
作為額外的預防措施，使用者可以讓每次交易都生成一個新的地址，以確保這些交易不被追溯到一個共同的所有者。但是由於並行輸入的存在，一定程度上的追溯還是不可避免的，因為並行輸入表明這些貨幣都屬於同一個所有者。此時的風險在於，如果某個人的某一個公鑰被確認屬於他，那麼就可以追溯出此人的其它很多交易。

11. 計算

設想如下場景：一個攻擊者試圖比誠實節點產生鏈條更快地製造替代性區塊鏈。即便它達到了這一目的，但是整個系統也並非就此完全受制於攻擊者的獨斷意志了，比方說憑空創造價值，或者掠奪本不屬於攻擊者的貨幣。這是因為節點將不會接受無效的交易，而誠實的節點永遠不會接受一個包含了無效資訊的區塊。一個攻擊者能做的，最多是更改他自己的交易資訊，並試圖拿回他剛剛付給別人的錢。
誠實鏈條和攻擊者鏈條之間的競賽，可以用二叉樹隨機漫步（Binomial Random Walk)來描述。成功事件定義為誠實鏈條延長了一個區塊，使其領先性+1，而失敗事件則是攻擊者的鏈條被延長了一個區塊，使得差距-1。
攻擊者成功填補某一既定差距的可能性，可以近似地看做賭徒破產問題（Gambler’s Ruin problem）。假定一個賭徒擁有無限的透支信用，然後開始進行潛在次數為無窮的賭博，試圖填補上自己的虧空。那麼我們可以計算他填補上虧空的概率，也就是該攻擊者趕上誠實鏈條，如下所示[8] ：

假定p>q，那麼攻擊成功的概率就因為區塊數的增長而呈現指數化下降。由於概率是攻擊者的敵人，如果他不能幸運且快速地獲得成功，那麼他獲得成功的機會隨著時間的流逝就變得愈發渺茫。那麼我們考慮一個收款人需要等待多長時間，才能足夠確信付款人已經難以更改交易了。我們假設付款人是一個支付攻擊者，希望讓收款人在一段時間內相信他已經付過款了，然後立即將支付的款項重新支付給自己。雖然收款人屆時會發現這一點，但為時已晚。
收款人生成了新的一對金鑰組合，然後只預留一個較短的時間將公鑰傳送給付款人。這將可以防止以下情況：付款人預先準備好一個區塊鏈然後持續地對此區塊進行運算，直到運氣讓他的區塊鏈超越了誠實鏈條，方才立即執行支付。當此情形，只要交易一旦發出，攻擊者就開始祕密地準備一條包含了該交易替代版本的平行鏈條。
然後收款人將等待交易出現在首個區塊中，然後在等到z個區塊連結其後。此時，他仍然不能確切知道攻擊者已經進展了多少個區塊，但是假設誠實區塊將耗費平均預期時間以產生一個區塊，那麼攻擊者的潛在進展就是一個泊松分佈，分佈的期望值為：

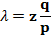
當此情形，為了計算攻擊者追趕上的概率，我們將攻擊者取得進展區塊數量的泊松分佈的概率密度，乘以在該數量下攻擊者依然能夠追趕上的概率。

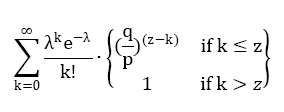
化為如下形式，避免對無限數列求和：

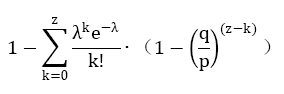
寫為如下C語言程式碼：

#include double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}

對其進行運算，我們可以得到如下的概率結果，發現概率對z值呈指數下降。
當q=0.1時
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
當q=0.3時
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
求解令P<0.1%的z值：
為使P<0.001，則
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340

12.結論

我們在此提出了一種不需要信用中介的電子支付系統。我們首先討論了通常的電子貨幣的電子簽名原理，雖然這種系統為所有權提供了強有力的控制，但是不足以防止雙重支付。為了解決這個問題，我們提出了一種採用工作量證明機制的點對點網路來記錄交易的公開資訊，只要誠實的節點能夠控制絕大多數的CPU計算能力，就能使得攻擊者事實上難以改變交易記錄。該網路的強健之處在於它結構上的簡潔性。節點之間的工作大部分是彼此獨立的，只需要很少的協同。每個節點都不需要明確自己的身份，由於交易資訊的流動路徑並無任何要求，所以只需要盡其最大努力傳播即可。節點可以隨時離開網路，而想重新加入網路也非常容易，因為只需要補充接收離開期間的工作量證明鏈條即可。節點通過自己的CPU計算力進行投票，表決他們對有效區塊的確認，他們不斷延長有效的區塊鏈來表達自己的確認，並拒絕在無效的區塊之後延長區塊以表示拒絕。本框架包含了一個P2P電子貨幣系統所需要的全部規則和激勵措施。
註釋 (↵ returns to text)
W Dai（戴偉）,a scheme for a group of untraceable digital pseudonyms to pay each other with money and to enforce contracts amongst themselves without outside help（一種能夠藉助電子假名在群體內部相互支付並迫使個體遵守規則且不需要外界協助的電子現金機制）, “B-money”, http://www.weidai.com/bmoney.txt, 1998↵
H. Massias, X.S. Avila, and J.-J. Quisquater, “Design of a secure timestamping service with minimal trust requirements,”（在最小化信任的基礎上設計一種時間戳伺服器） In 20th Symposium on Information Theory in the Benelux, May 1999.↵
S. Haber, W.S. Stornetta, “How to time-stamp a digital document,” （怎樣為電子檔案新增時間戳）In Journal of Cryptology, vol 3, No.2, pages 99-111, 1991.↵
D. Bayer, S. Haber, W.S. Stornetta, “Improving the efficiency and reliability of digital time-stamping,”（提升電子時間戳的效率和可靠性） In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.↵
S. Haber, W.S. Stornetta, “Secure names for bit-strings,”（位元字串的安全命名） In Proceedings of the 4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997. on Computer and Communications Security, pages 28-35, April 1997.↵
A. Back, “Hashcash – a denial of service counter-measure,”（雜湊現金——拒絕服務式攻擊的剋制方法）http://www.hashcash.org/papers/hashcash.pdf, 2002.↵
R.C. Merkle, “Protocols for public key cryptosystems,” （公鑰密碼系統的協議）In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.
S. Haber, W.S. Stornetta, “Secure names for bit-strings,”（位元字串安全命名） In Proceedings of the 4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997. on Computer and Communications Security, pages 28-35, April 1997.
H. Massias, X.S. Avila, and J.-J. Quisquater, “Design of a secure timestamping service with minimal trust requirements,”（在最小化信任的條件下設計一種時間戳伺服器） In 20th Symposium on Information Theory in the Benelux, May 1999.↵
W. Feller, “An introduction to probability theory and its applications,” （概率學理論與應用導論）1957↵