光明小學的小朋友們要舉行一年一度的接力跑大賽了，但是小朋友們卻遇到了一個難題：設計接力跑大賽的線路，你能幫助他們完成這項工作麼？
光明小學可以抽象成一張有N個節點的圖，每兩點間都有一條道路相連。光明小學的每個班都有M個學生，所以你要為他們設計出一條恰好經過M條邊的路徑。
光明小學的小朋友們希望全盤考慮所有的因素，所以你需要把任意兩點間經過M條邊的最短路徑的距離輸出出來以供參考。

你需要設計這樣一個函式：
res[][] Solve( N, M, map[][]);
注意：map必然是N * N的二維陣列，且map[i][j] == map[j][i]，map[i][i] == 0，-1e8 <= map[i][j] <= 1e8。（道路全部是無向邊，無自環）2 <= N <= 100, 2 <= M <= 1e6。要求時間複雜度控制在O(N^3*log(M))。

map陣列表示了一張稠密圖，其中任意兩個不同節點i,j間都有一條邊，邊的長度為map[i][j]。N表示其中的節點數。
你要返回的陣列也必然是一個N * N的二維陣列，表示從i出發走到j，經過M條邊的最短路徑
你的路徑中應考慮包含重複邊的情況。

樣例：
N = 3
M = 2
map = {
{0, 2, 3},
{2, 0, 1},
{3, 1, 0}
}

輸出結果result為：
result = {
{4, 4, 3},
{4, 2, 5},
{3, 5, 2}
}

輸入樣例：
3
2
3 3
0 2 3
2 0 1
3 1 0

輸出樣例：
4 4 3
4 2 5
3 5 2

分析：

首先，假設從 i 到 j 經過(m-1)條邊的最短距離已知，儲存在last_opt[n][n]二維陣列中。那麼從 i 到 j 經過m條邊的最短距離簡化成：

dp_opt=min(last_opt [i] [x] + map [x] [j] )

經過m條邊的最短路徑只和最後一步的路徑以及走（m-1）步的最短路徑有關，map [x] [j] 表示最後一步，last_opt [i] [x] 表示從起點 i 走m-1 步到x的最短路徑。

附上Python 3 程式碼，時間複雜度 O（n^3*(m-1)）//我不會算時間複雜度呀，這裡可能算錯了

空間複雜度O（2*n*n）

def minPath(n,m,map):
    last_opt=[list(x) for x in map]#初始化
    dp_opt=[list(x) for x in map]#初始化
    for step in range(m-1):#只需要迴圈 m-1次
        for i in range(n):
            for j in range(n):
                temp = [last_opt[i][x] + map[x][j] for x in range(n) if map[x][j]!=0 and last_opt[i][x]!=0] #遞推式轉換 注意判斷條件
                dp_opt[i][j] = min(temp)#取所有情況中的最小值
        last_opt=[list(x) for x in dp_opt]#拷貝以待下次迴圈
    return dp_opt


if __name__ == '__main__':
    n = int(input())
    m = int(input())
    x=input()
    map = []
    for i in range(n):
        map.append([int(x) for x in input().split()])
    res=minPath(n,m,map)
    for x in res:
        print(x)
 

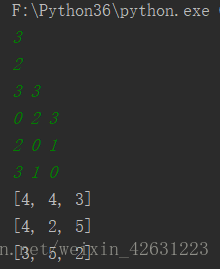
來看看測試結果：

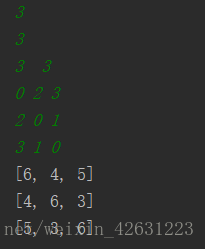
再來看看m=3的結果：

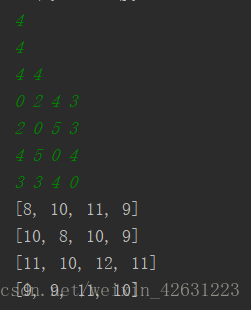
再來看看n=4 的結果：

因為道路是無向的，所以從 i 到 j 走m步的最短距離肯定和從 j 到 i 走m步的最短距離相等，所以輸出一定是一個對稱矩陣，如果不是對稱的，一定是哪裡邏輯出錯了……

如果有人搜到這篇部落格，然後複製我的程式碼上去，可能會發現程式碼測試通過率為0，那是因為要求的輸出是數字，但是這裡輸出的dp_opt是一個列表，是帶方括號的，和題目要求不符，記得自己改下程式碼，挨個輸出就行了。

C++程式碼有空再寫。

嚶嚶嚶，第一次自己做出來的動態規劃題，雖然測試的時候沒做出來……umm當自我安慰吧。