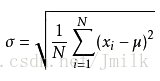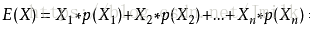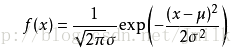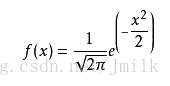前言

首先借機回答一下讀者小夥伴的問題，計算原理、組合和排列的現實意義是什麼？學習數學對從事 IT 行業而言有什麼幫助？

實話說，這些問題應該是普遍存在的，曾經是我的問題，也可能會成為你的問題。歡迎大家在評論區裡說說自己的看法。

• 計數原理：又稱基本計數原理，它將實現一個目標的行為抽象成 分步 和 分類 兩種，正如計數原理中給出的例子。計數原理通過這兩種計數規則為解決現實生活中大多數的計數問題提供了思路和工具。所謂計數，其目的是為了求解出一個「總數」，比如：完成一件事情所擁有的全部做法；達到一個目的所擁有的全部可能。

• 組合與排列：求解的是 特定集合空間裡所擁有的元素之間的組合和排列的可能性

  ，是一個特定條件下的「總數」，所以在組合與排列文中推導公式時就引入了計算原理。組合與排列是概率論中重要的基礎，因為其求解的總數，常被作為概率結果中的分母。

• 至於學習數學對從事 IT 行業有什麼實際上的作用？就當下而言，對大資料和人工智慧方向的研究很有用，數理基礎不紮實容易事倍功半，至於別的研究方向就要各憑興趣愛好。對未來而言，筆者不相信計算機應用的未來，但相信電腦科學的未來，所以為了以後更好適應行業的發展，需要作出長遠準備。

統計與分佈

統計和分佈的核心在於「描述」，用簡明且可操作的方式直觀展現大量樣本的巨集觀樣態，這是統計與分佈所解決的主要問題之一。

使用單一資料定義來概括性描述一些抽象或複雜資料的方式，即為統計學指標

• 加和值：使用加和值來描述問題最大的好處是直奔主題，忽略個體樣本細節。比如超市結賬，我們只需要知道總共需要付多少錢，而無須關心每一件商品的價格。

• 平均值：使用平均值能夠對整體樣本有一個概括性的描述，同時也能兼具對每個個體樣本的描述。比如某個人的成績是低於還是高於整體平均值。

• 眾數：使用眾數能夠描述整體樣本的偏好特徵。比如小明每週要看 5 場電影，其中喜劇看了 3 場，為眾數，可以看出小明對喜劇電影的偏好。

• 中位數：使用中位數能夠描述樣本的分佈特徵，在一定程度上可以消除個別極端的個體樣本值對整體樣本平均值的影響。將樣本集中的極端值剔除，然後求得的平均值往往會更加接近中位數。

標準差

使用標準差能夠描述個體樣本與整體樣本平均值之間的差異，差異值越大，表示個體與整體平均線的離散型（正、反差異）越大。

標準差公式：

• 其中 (x - μ)^2 表示個體樣本 x 與整體均值的離差，因為離差只能是正數，所以求平方。

可見，標準差是一組資料平均值分散程度的度量。

加權均值

加權平均值是一種特殊的平均值，現實中很多問題的均值結果不僅取決於個體樣本標準值的大小，而且還取決於個體樣本標準值出現的次數（頻數），這些頻數同樣對最終的結果有著權衡輕重的作用，所以也將頻數叫做權重。

例如：一箱什錦糖裡混有牛奶糖 1斤 單價 10元、水果糖 2斤 單價 20元、巧克力糖 3斤 單價 30元，那麼求解什錦糖應該售賣多少錢一斤？

顯然這是一個求均值的問題，但卻不能使用普通平均值演算法求解，而是應該使用加權平均值演算法，因為 3 種糖果在樣本集(箱)中的權重是不同的。

• 平均值：(10+20+30)/6=10元/斤
• 加權平均值：(10*1+20*2+30*3)/6 約為 23元/斤

加權平均值公式：累加各個體樣本標準值與權重的乘積，再除以個體單位數量。
（其中 f1, f2, …, fk 表示權重）

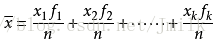
數學期望

數學期望，又稱均值，或簡稱期望，是指在一個隨機變數試驗中每次可能結果的概率乘以其結果的總和，即累加各個體樣本標準值與個體樣本概率的乘積。期望描述的是隨機變數平均取值的大小。

數學期望公式：

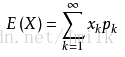
當 Xn(n=1, 2, …, k) 的概率均 1/k 時，數學期望即為平均數。實際上在很多場景中的平均值和期望往往是接近的，但兩者又有著區別。

• 平均值：針對的是小量樣本集，能夠輕易的進行全加和然後再除以單位數。所以得到的結果是準確的，不會有模糊概念。
• 期望：則針對大量樣本集，無法輕易實現全加和，只好應用抽樣方法。首先得出抽樣個體及其出現的概率，然後再加和計算。透過抽樣均值，去預測全樣本空間的均值，所以稱為期望值。

高斯分佈

高斯分佈，又名正態分佈，是一種 概率分佈，屬概率論學科，對統計學的許多方面都有著非常重要的影響。

概率密度函式：

• f(x) 中的 x 是一個樣本特性自變數
• f(x) 則表示擁有樣本特性 x 的個體樣本數量所佔樣本總數的比例
• exp 指的是自然常數 e 的冪函式
• σ 表示標準差，σ^2 則為方差
• μ 表示平均值或數學期望

當 μ=0, σ=1 時，為標準正態分佈，x 為 0 時得峰值：

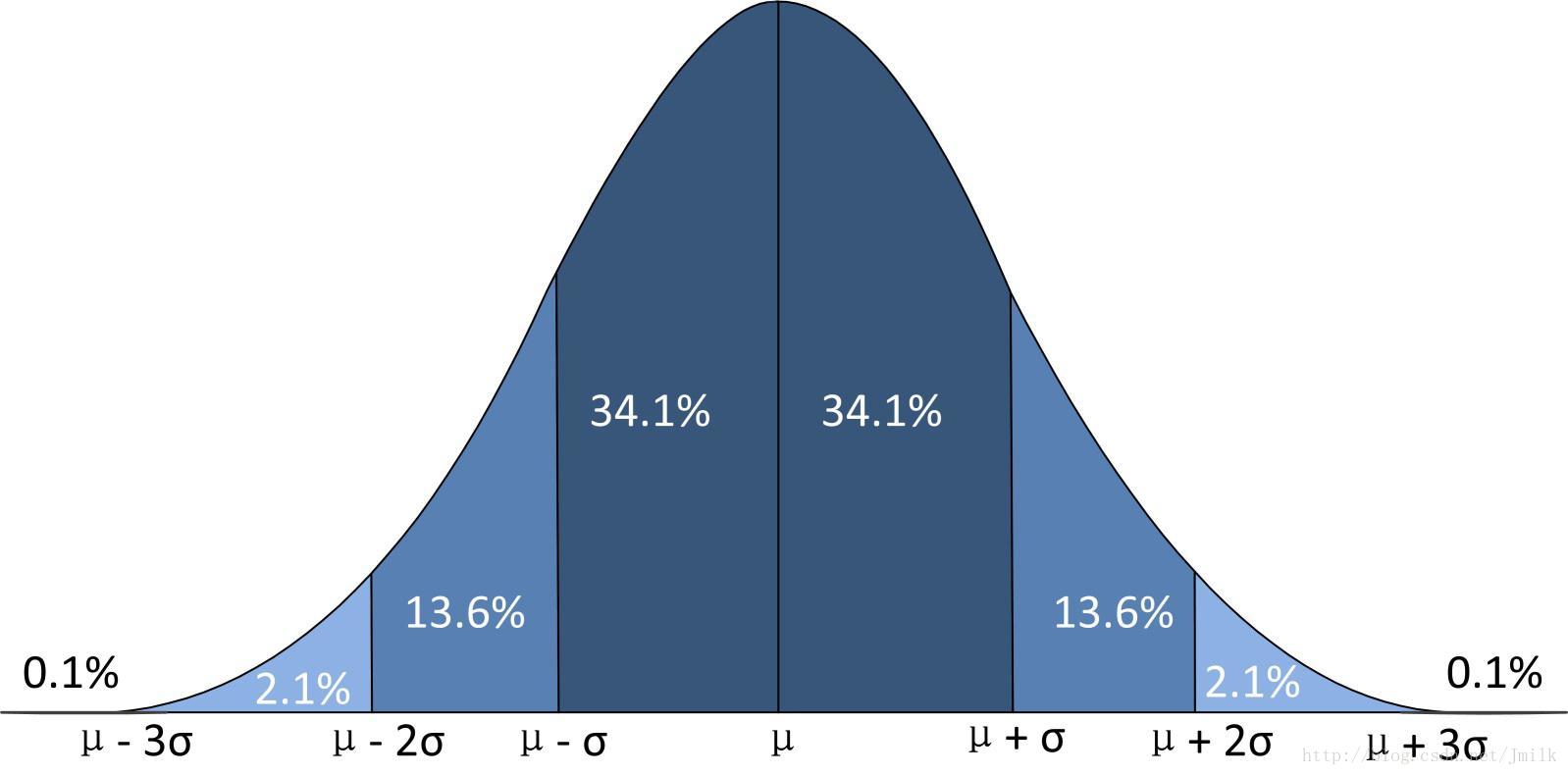
正態分佈曲線，又稱鍾型曲線：

正態分佈特性：
1. x=μ 時，得到曲線峰值
2. 以 x=μ 為中軸左右對稱
3. 屬於 [μ-σ, μ+σ] 區間的樣本特性的樣本數量比例為 68.2%
4. 屬於 [μ-2σ, μ+2σ] 區間的樣本特性的樣本數量比例為 95.4%
5. 屬於 [μ-3σ, μ+3σ] 區間的樣本特性的樣本數量比例為 99.6%
6. μ 越大麴線中軸就越向右移，反之向左
7. σ 越大麴線坡度就越扁平，反之陡峭

應用場景：
假如得知某高校男學生 1000 人，並且以及通過統計計算得出 μ=175，σ=10，那麼我們就可以輕易通過高斯密度曲線得出下述結果。

• 身高 165~175 大約 341 人
• 身高 155-165 大約 136 人
• 身高 145-155 大約 21 人

總的來說高斯分佈的適用場景有著一個共同特點 —— 一般般的很多，極端的很少。例如，智商很高或很低的人很少，智商一般般的人很多；非常有錢和非常貧窮的人很少，一般般有錢的人很多。可見高斯分佈的適用面是極其廣泛的，他能夠非常簡明的將各個區間的概率密度呈現出現。