來源

漢諾塔是來源於印度的一種古老的益智遊戲。它總共有三根柱子，分別為A，B，C。初始狀態下，Ａ柱中有N個盤子，這N個盤子有大有小，大的在下面，小的在上面。遊戲的最終目標就是將Ａ柱上的所有盤子移到Ｃ柱上，中間可以經過B柱，過程中必須保持大盤在下面，小盤在上面。如圖所示：

演算法引申

在這個題目中，我們把關注點投向最優解實現：需要用最少的步驟完成遊戲，移動的過程是怎麼樣的。
現在讓我們在腦海中想一下自己操作的時候會怎麼做？先來定義一下每根柱上的實時數目｛A:N, B:0, C:0｝
我們要把A柱上的N個盤移到C柱，就要先把A柱上面的N－1個盤移到B柱上，此時A柱上只有一個，狀態是｛A:1, B:N－1, C:0｝

F(n)=F(n-1)+F(1)+F(n-1)=2*f(n-1)+1

通過數學歸納法可以得到F（n）= 2^n+1
至此，我們解決了第一個問題，通過 （2^n＋1） 次移動，可以完成遊戲。

那麼移動的過程是怎樣的呢？
漢諾塔的移動只需要三步，前面已經分析過了，可以看出這是一個典型的遞迴函式，我們可以打印出移動的步驟：

python解法

# 漢諾塔移動，把n個盤將a移到c，途中經轉b
def move(n, a, b, c):
    if n == 1:
        print('move', a, '-->', c)  #根部迭代，一次情況下，直接 a --> c 移動 
        return
    move(n-1, a, c, b)              #把a中的n-1個盤移動到b，途中經轉c
    print('move', a, '-->'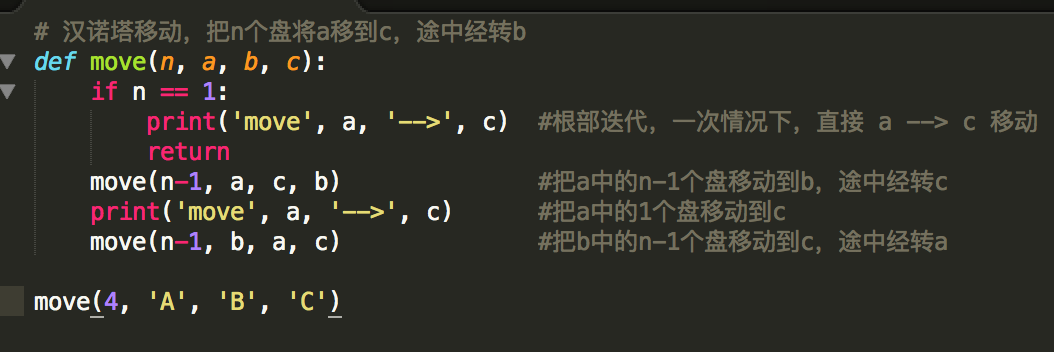
 
, c)      #把a中的1個盤移動到c
    move(n-1, b, a, c)              #把b中的n-1個盤移動到c，途中經轉a

move(4, 'A', 'B', 'C')

我們用python定義了一個move函式，它的第一個引數為需要移動的個數n，第二個引數為出發柱a，第三個引數為中轉柱b，第三個引數為目標柱c，完成的操作是從出發柱移動了n個盤子到目標柱

執行結果

漢諾塔的講解到這裡應該也比較清晰了，本質就是遞迴呼叫，最重要的一點是

漢諾塔的移動只需要三步