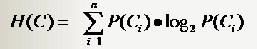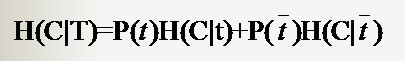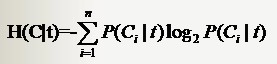（一）認識決策樹

1，決策樹分類原理

決策樹是通過一系列規則對資料進行分類的過程。它提供一種在什麼條件下會得到什麼值的類似規則的方法。決策樹分為分類樹和迴歸樹兩種，分類樹對離散變數做決策樹，迴歸樹對連續變數做決策樹。

近來的調查表明決策樹也是最經常使用的資料探勘演算法，它的概念非常簡單。決策樹演算法之所以如此流行，一個很重要的原因就是使用者基本上不用瞭解機器學習演算法，也不用深究它是如何工作的。直觀看上去，決策樹分類器就像判斷模組和終止塊組成的流程圖，終止塊表示分類結果（也就是樹的葉子）。判斷模組表示對一個特徵取值的判斷（該特徵有幾個值，判斷模組就有幾個分支）。

如果不考慮效率等，那麼樣本所有特徵的判斷級聯起來終會將某一個樣本分到一個類終止塊上。實際上，樣本所有特徵中有一些特徵在分類時起到決定性作用，決策樹的構造過程就是找到這些具有決定性作用的特徵，根據其決定性程度來構造一個倒立的樹--決定性作用最大的那個特徵作為根節點，然後遞迴找到各分支下子資料集中次大的決定性特徵，直至子資料集中所有資料都屬於同一類。所以，構造決策樹的過程本質上就是根據資料特徵將資料集分類的遞迴過程，我們需要解決的第一個問題就是，當前資料集上哪個特徵在劃分資料分類時起決定性作用。

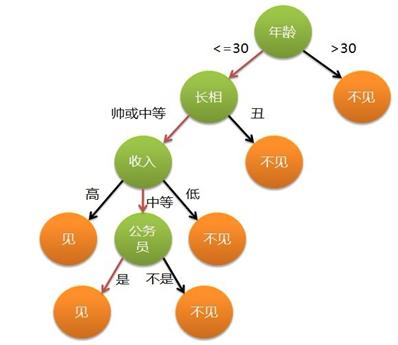
為了找到決定性的特徵、劃分出最好的結果，我們必須評估資料集中蘊含的每個特徵，尋找分類資料集的最好特徵。完成評估之後，原始資料集就被劃分為幾個資料子集。這些資料子集會分佈在第一個決策點的所有分支上。如果某個分支下的資料屬於同一型別，則則該分支處理完成，稱為一個葉子節點，即確定了分類。如果資料子集內的資料不屬於同一型別，則需要重複劃分資料子集的過程。如何劃分資料子集的演算法和劃分原始資料集的方法相同，直到所有具有相同型別的資料均在一個數據子集內（葉子節點）。如下圖就是一個決策樹例項（目標是兩類--見或者不見，每個樣本有年齡、長相、收入、是否公務員四個特徵）：

2， 決策樹的學習過程

一棵決策樹的生成過程主要分為以下3個部分:

特徵選擇：特徵選擇是指從訓練資料中眾多的特徵中選擇一個特徵作為當前節點的分裂標準，如何選擇特徵有著很多不同量化評估標準標準，從而衍生出不同的決策樹演算法。

決策樹生成： 根據選擇的特徵評估標準，從上至下遞迴地生成子節點，直到資料集不可分則停止決策樹停止生長。 樹結構來說，遞迴結構是最容易理解的方式。

剪枝：決策樹容易過擬合，一般來需要剪枝，縮小樹結構規模、緩解過擬合。剪枝技術有預剪枝和後剪枝兩種。

3，基於資訊理論的三種決策樹演算法

劃分資料集的最大原則是：使無序的資料變的有序。如果一個訓練資料中有20個特徵，那麼選取哪個做劃分依據？這就必須採用量化的方法來判斷，量化劃分方法有多重，其中一項就是“資訊理論度量資訊分類”。基於資訊理論的決策樹演算法有ID3、CART和C4.5等演算法，其中C4.5和CART兩種演算法從ID3演算法中衍生而來。

CART和C4.5支援資料特徵為連續分佈時的處理，主要通過使用二元切分來處理連續型變數，即求一個特定的值-分裂值：特徵值大於分裂值就走左子樹，或者就走右子樹。這個分裂值的選取的原則是使得劃分後的子樹中的“混亂程度”降低，具體到C4.5和CART演算法則有不同的定義方式。

ID3演算法由Ross Quinlan發明，建立在“奧卡姆剃刀”的基礎上：越是小型的決策樹越優於大的決策樹（be simple簡單理論）。ID3演算法中根據資訊理論的資訊增益評估和選擇特徵，每次選擇資訊增益最大的特徵做判斷模組。ID3演算法可用於劃分標稱型資料集，沒有剪枝的過程，為了去除過度資料匹配的問題，可通過裁剪合併相鄰的無法產生大量資訊增益的葉子節點（例如設定資訊增益閥值）。使用資訊增益的話其實是有一個缺點，那就是它偏向於具有大量值的屬性--就是說在訓練集中，某個屬性所取的不同值的個數越多，那麼越有可能拿它來作為分裂屬性，而這樣做有時候是沒有意義的，另外ID3不能處理連續分佈的資料特徵，於是就有了C4.5演算法。CART演算法也支援連續分佈的資料特徵。

C4.5是ID3的一個改進演算法，繼承了ID3演算法的優點。C4.5演算法用資訊增益率來選擇屬性，克服了用資訊增益選擇屬性時偏向選擇取值多的屬性的不足在樹構造過程中進行剪枝；能夠完成對連續屬性的離散化處理；能夠對不完整資料進行處理。C4.5演算法產生的分類規則易於理解、準確率較高；但效率低，因樹構造過程中，需要對資料集進行多次的順序掃描和排序。也是因為必須多次資料集掃描，C4.5只適合於能夠駐留於記憶體的資料集。

CART演算法的全稱是Classification And Regression Tree，採用的是Gini指數（選Gini指數最小的特徵s）作為分裂標準,同時它也是包含後剪枝操作。ID3演算法和C4.5演算法雖然在對訓練樣本集的學習中可以儘可能多地挖掘資訊，但其生成的決策樹分支較大，規模較大。為了簡化決策樹的規模，提高生成決策樹的效率，就出現了根據GINI係數來選擇測試屬性的決策樹演算法CART。

4，決策樹優缺點

決策樹適用於數值型和標稱型（離散型資料，變數的結果只在有限目標集中取值），能夠讀取資料集合，提取一些列資料中蘊含的規則。在分類問題中使用決策樹模型有很多的優點，決策樹計算複雜度不高、便於使用、而且高效，決策樹可處理具有不相關特徵的資料、可很容易地構造出易於理解的規則，而規則通常易於解釋和理解。決策樹模型也有一些缺點，比如處理缺失資料時的困難、過度擬合以及忽略資料集中屬性之間的相關性等。

（二）ID3演算法的數學原理

前面已經提到C4.5和CART都是由ID3演化而來，這裡就先詳細闡述ID3演算法，奠下基礎。

1，ID3演算法的資訊理論基礎

關於決策樹的資訊理論基礎可以參考“決策樹1-建模過程”

（1）資訊熵

資訊熵：在概率論中，資訊熵給了我們一種度量不確定性的方式，是用來衡量隨機變數不確定性的，熵就是資訊的期望值。若待分類的事物可能劃分在N類中，分別是x₁，x₂，……，x_n，每一種取到的概率分別是P₁，P₂，……，P_n，那麼X的熵就定義為：

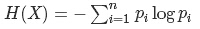，從定義中可知:0≤H(X)≤log(n)

當隨機變數只取兩個值時，即X的分佈為 P(X=1)=p,X(X=0)=1−p,0≤p≤1則熵為:H(X)=−plog₂(p)−(1−p)log₂(1−p)。

熵值越高，則資料混合的種類越高，其蘊含的含義是一個變數可能的變化越多（反而跟變數具體的取值沒有任何關係，只和值的種類多少以及發生概率有關），它攜帶的資訊量就越大。熵在資訊理論中是一個非常重要的概念，很多機器學習的演算法都會利用到這個概念。

(2)條件熵

假設有隨機變數(X,Y)，其聯合概率分佈為:P(X=xi,Y=yi)=pij,i=1,2,⋯,n;j=1,2,⋯,m

則條件熵(H(Y∣X))表示在已知隨機變數X的條件下隨機變數Y的不確定性，其定義為X在給定條件下Y的條件概率分佈的熵對X的數學期望:

    
 

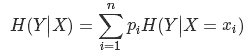
（3）資訊增益

資訊增益(information gain)表示得知特徵X的資訊後，而使得Y的不確定性減少的程度。定義為:

     

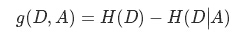
2，ID3演算法推導

(1)分類系統資訊熵

假設一個分類系統的樣本空間（D,Y），D表示樣本（有m個特徵），Y表示n個類別，可能的取值是C₁，C_2，...，C_n。每一個類別出現的概率是P(C₁)，P(C₂)，...，P(C_n)。該分類系統的熵為：

離散分佈中，類別C_i出現的概率P(C_i)，通過該類別出現的次數除去樣本總數即可得到。對於連續分佈，常需要分塊做離散化處理獲得。

(2)條件熵

根據條件熵的定義,分類系統中的條件熵指的是當樣本的某一特徵X固定時的資訊熵。由於該特徵X可能的取值會有（x₁，x₂，……，x_n），當計算條件熵而需要把它固定的時候，每一種可能都要固定一下，然後求統計期望。

因此樣本特徵X取值為x_i的概率是P_i，該特徵被固定為值x_i時的條件資訊熵就是H(C|X=xi)，那麼

H(C|X)就是分類系統中特徵X被固定時的條件熵（X=（x₁，x₂，……，x_n））：

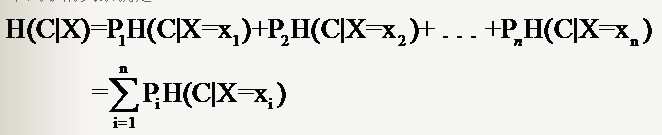
若是樣本的該特徵只有兩個值（x₁ = 0,x₂=1）對應(出現，不出現)，如文字分類中某一個單詞的出現與否。那麼對於特徵二值的情況，我們用T代表特徵，用t代表T出現，表示該特徵出現。那麼：

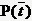
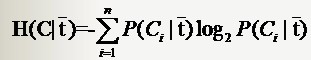
與前面條件熵的公式對比一下，P(t)就是T出現的概率，就是T不出現的概率。結合資訊熵的計算公式，可得：

     

特徵T出現的概率P(t)，只要用出現過T的樣本數除以總樣本數就可以了；P(C_i|t)表示出現T的時候，類別C_i出現的概率，只要用出現了T並且屬於類別C_i的樣本數除以出現了T的樣本數就得到了。

（3）資訊增益

根據資訊增益的公式，分類系統中特徵X的資訊增益就是：Gain(D, X) = H(C)-H(C|X)

資訊增益是針對一個一個的特徵而言的，就是看一個特徵X，系統有它和沒它的時候資訊量各是多少，兩者的差值就是這個特徵給系統帶來的資訊增益。每次選取特徵的過程都是通過計算每個特徵值劃分資料集後的資訊增益，然後選取資訊增益最高的特徵。

對於特徵取值為二值的情況，特徵T給系統帶來的資訊增益就可以寫成系統原本的熵與固定特徵T後的條件熵之差：

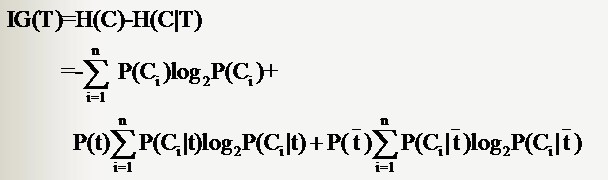
(4)經過上述一輪資訊增益計算後會得到一個特徵作為決策樹的根節點，該特徵有幾個取值，根節點就會有幾個分支，每一個分支都會產生一個新的資料子集D_k，餘下的遞迴過程就是對每個D_k再重複上述過程，直至子資料集都屬於同一類。

在決策樹構造過程中可能會出現這種情況：所有特徵都作為分裂特徵用光了，但子集還不是純淨集（集合內的元素不屬於同一類別）。在這種情況下，由於沒有更多資訊可以使用了，一般對這些子集進行“多數表決”，即使用此子集中出現次數最多的類別作為此節點類別，然後將此節點作為葉子節點。

（三）C4.5演算法

1，資訊增益比選擇最佳特徵

以資訊增益進行分類決策時，存在偏向於取值較多的特徵的問題。於是為了解決這個問題人們有開發了基於資訊增益比的分類決策方法，也就是C4.5。C4.5與ID3都是利用貪心演算法進行求解，不同的是分類決策的依據不同。

因此，C4.5演算法在結構與遞迴上與ID3完全相同，區別就在於選取決斷特徵時選擇資訊增益比最大的。

資訊增益比率度量是用ID3演算法中的的增益度量Gain(D，X)和分裂資訊度量SplitInformation(D，X)來共同定義的。分裂資訊度量SplitInformation(D，X）就相當於特徵X（取值為x₁，x₂，……，x_n，各自的概率為P₁，P₂，...，P_n，P_k就是樣本空間中特徵X取值為x_k的數量除上該樣本空間總數）的熵。

SplitInformation(D，X） = -P₁ log₂(P₁)-P₂ log₂(P)-,...,-P_n log₂(P_n)

GainRatio(D,X) = Gain(D,X)/SplitInformation(D,X)

在ID3中用資訊增益選擇屬性時偏向於選擇分枝比較多的屬性值，即取值多的屬性，在C4.5中由於除以SplitInformation(D,X)=H(X)，可以削弱這種作用。

2，處理連續數值型特徵

C4.5既可以處理離散型屬性，也可以處理連續性屬性。在選擇某節點上的分枝屬性時，對於離散型描述屬性，C4.5的處理方法與ID3相同。對於連續分佈的特徵，其處理方法是：

先把連續屬性轉換為離散屬性再進行處理。雖然本質上屬性的取值是連續的，但對於有限的取樣資料它是離散的，如果有N條樣本，那麼我們有N-1種離散化的方法：<=v_j的分到左子樹，>v_j的分到右子樹。計算這N-1種情況下最大的資訊增益率。另外，對於連續屬性先進行排序（升序），只有在決策屬性（即分類發生了變化）發生改變的地方才需要切開，這可以顯著減少運算量。經證明，在決定連續特徵的分界點時採用增益這個指標（因為若採用增益率，splittedinfo影響分裂點資訊度量準確性，若某分界點恰好將連續特徵分成數目相等的兩部分時其抑制作用最大），而選擇屬性的時候才使用增益率這個指標能選擇出最佳分類特徵。

在C4.5中，對連續屬性的處理如下：

1.      對特徵的取值進行升序排序

2.      兩個特徵取值之間的中點作為可能的分裂點，將資料集分成兩部分，計算每個可能的分裂點的資訊增益（InforGain）。優化演算法就是隻計算分類屬性發生改變的那些特徵取值。

3.      選擇修正後資訊增益(InforGain)最大的分裂點作為該特徵的最佳分裂點

4.      計算最佳分裂點的資訊增益率（Gain Ratio）作為特徵的Gain Ratio。注意，此處需對最佳分裂點的資訊增益進行修正：減去log2(N-1)/|D|（N是連續特徵的取值個數，D是訓練資料數目，此修正的原因在於：當離散屬性和連續屬性並存時，C4.5演算法傾向於選擇連續特徵做最佳樹分裂點）

實現連續特徵資料集劃分的Python程式為：

1. def binSplitDataSet(dataSet, feature, value):   
2.     mat0 = dataSet[nonzero(dataSet[:,feature] > value)[0],:][0]   
3.     mat1 = dataSet[nonzero(dataSet[:,feature] <= value)[0],:][0]   
4.     return mat0,mat1  

其中dataset為numpy matrix， feature為dataset連續特徵在dataset所有特徵中的index，value即為feature臨近兩值的均值。

3，葉子裁剪

分析分類迴歸樹的遞迴建樹過程，不難發現它實質上存在著一個數據過度擬合問題。在決策樹構造時，由於訓練資料中的噪音或孤立點，許多分枝反映的是訓練資料中的異常，使用這樣的判定樹對類別未知的資料進行分類，分類的準確性不高。因此試圖檢測和減去這樣的分支，檢測和減去這些分支的過程被稱為樹剪枝。樹剪枝方法用於處理過分適應資料問題。通常，這種方法使用統計度量，減去最不可靠的分支，這將導致較快的分類，提高樹獨立於訓練資料正確分類的能力。

決策樹常用的剪枝常用的簡直方法有兩種：預剪枝(Pre-Pruning)和後剪枝(Post-Pruning)。預剪枝是根據一些原則及早的停止樹增長，如樹的深度達到使用者所要的深度、節點中樣本個數少於使用者指定個數、不純度指標下降的最大幅度小於使用者指定的幅度等。預剪枝的核心問題是如何事先指定樹的最大深度，如果設定的最大深度不恰當，那麼將會導致過於限制樹的生長，使決策樹的表示式規則趨於一般，不能更好地對新資料集進行分類和預測。除了事先限定決策樹的最大深度之外，還有另外一個方法來實現預剪枝操作，那就是採用檢驗技術對當前結點對應的樣本集合進行檢驗，如果該樣本集合的樣本數量已小於事先指定的最小允許值，那麼停止該結點的繼續生長，並將該結點變為葉子結點，否則可以繼續擴充套件該結點。

後剪枝則是通過在完全生長的樹上剪去分枝實現的，通過刪除節點的分支來剪去樹節點，可以使用的後剪枝方法有多種，比如：代價複雜性剪枝、最小誤差剪枝、悲觀誤差剪枝等等。後剪枝操作是一個邊修剪邊檢驗的過程，一般規則標準是：在決策樹的不斷剪枝操作過程中，將原樣本集合或新資料集合作為測試資料，檢驗決策樹對測試資料的預測精度，並計算出相應的錯誤率，如果剪掉某個子樹後的決策樹對測試資料的預測精度或其他測度不降低，那麼剪掉該子樹。

（三）Python實現ID3、C4.5演算法決策樹

Python中不需要構造新的資料型別來儲存決策樹，使用字典dict即可方便的儲存節點資訊，永久儲存則可以通過pickle或者JSON將決策樹字典寫入檔案中，本包採用JSON。包中trees模組定義了一個decisionTree物件，同時支援ID3和C4.5兩種演算法（C4.5演算法連續特徵的處理和後剪枝沒有實現），該物件中的屬性如函式__init__中所示：

1. class decisionTree(object):   
2.     def __init__(self,dsDict_ID3 = None,dsDict_C45 = None, features = None, **args):   
3.         '''currently support ID3 and C4.5, the default type is C4.5, CART TBD 
4.         '''  
5.         obj_list = inspect.stack()[1][-2]   
6.         self.__name__ = obj_list[0].split('=')[0].strip()   
7.         self.dsDict_ID3 = dsDict_ID3   
8.         self.dsDict_C45 = dsDict_C45   
9.         #self.classLabel = classLabel  
10.         self.features = features  

decisionTree物件的train函式的輸入資料為樣本列表和樣本特徵列表，其中樣本列表每個元素的最後一項表示該元素的分類，格式如下所示：

1. dataSet = [[1,1,'yes'],   
2.                [1,1,'yes'],   
3.                [1,0,'no'],   
4.                [0,1,'no'],   
5.                [0,1,'no']   
6.               ]   
7. labels = ['no surfacing', 'flippers']  

另外，通過Python的Matplotlib的註解功能則可以繪製樹形圖，方便展示。decisionTree物件提供了treePlot方法，通過模組treePlotter中的函式實現。

testDS模組則採用決策樹決定患者是否能夠佩戴隱形眼鏡，需要考慮的特徵因素包括四個--'age', 'prescript', 'astigmatic', 'tearRate'。下圖就是利用decisionTree物件生成的決策樹。

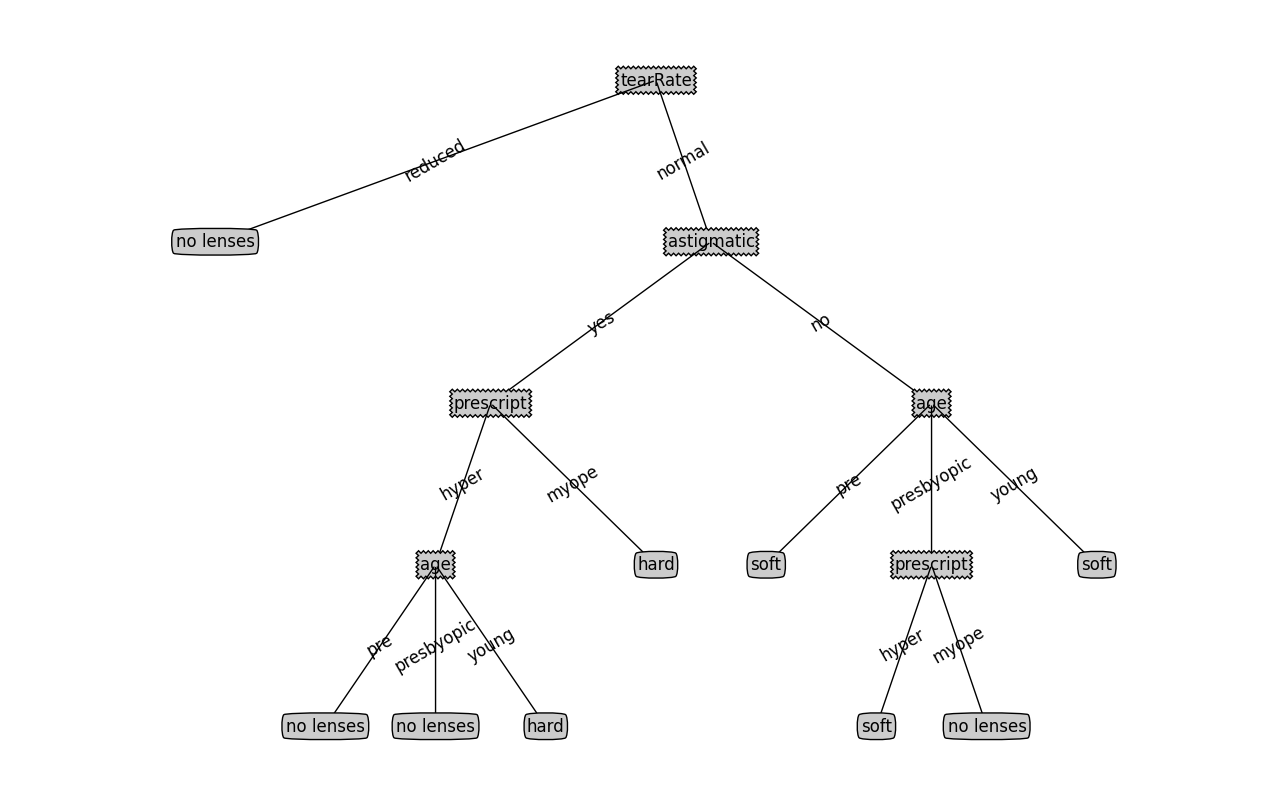
決策樹演算法學習包下載地址：

（四）決策樹應用

決策樹技術在資料化運營中的主要用途體現在：作為分類、預測問題的典型支援技術，它在使用者劃分、行為預測、規則梳理等方面具有廣泛的應用前景。

參考