【機器學習演算法-python實現】svm支援向量機(3)—核函式
阿新 • • 發佈:2019-01-08
1.背景知識
前面我們提到的資料集都是線性可分的,這樣我們可以用SMO等方法找到支援向量的集合。然而當我們遇到線性不可分的資料集時候,是不是svm就不起作用了呢?這裡用到了一種方法叫做核函式,它將低維度的資料轉換成高緯度的從而實現線性可分。 可能有的人不明白為什麼低維度的資料集轉換成高維度的就可以實現線性可分,下面摘抄一個網上的例子解釋一下。看下面這個圖,我們設紅色的區域是一組資料 ,而直線ab除了紅色區域以外是另一組資料。因為直線是一維的,所以我們無法找到一條直線區分這兩組資料。單是當我們把這組資料引入二維之後,我們可以得到一組曲線,它在ab直線上部分指向黑色直線部分,ab直線下部指向紅色部分。
我們通過這個例子可以看到核函式的作用,因為svm的結果只跟向量內積有關係,所以我們可以配合核函式實現任意資料集的分類。如果有人問,如果就是有一定的點數使得我們無論增加多少維度都不能實現分類,這就是引用鬆弛變數的意義,忽略這一部分點,因為它們很有可能是噪聲。
2.程式碼部分
因為核函式有很多種類,比較常用的就是徑向基核函式(RBF),這個準確率是比較高的。公式: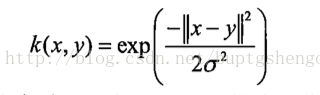
K = exp(K/(-1*kTup[1]**2))