模式分類與應用-貝葉斯垃圾郵件分類
垃圾郵件分類
任務要求
使用檔案spambase.data中的資料,訓練垃圾郵件分類的貝葉斯分類器,並測試分類效能。
資料初步分析
spambase.data是一個垃圾郵件的資料庫,來自於惠普公司的Hewlett Packard Labs實驗室,採集時間是1999年的6~7月份。
該資料庫中包含了4601個樣本,其中1813條為垃圾郵件(spam);每個樣本有58個屬性。在資料檔案中,每行為一個樣本,58個屬性按順序排列,使用","分隔。格式如下:
圖 21 資料檔案的格式
各屬性的含義和數值範圍如下表所列:
表格 21 樣本屬性說明
|
屬性序號 |
含義 |
範圍 |
最大值 |
|
1-48 |
特定單詞的出現頻率 |
[0, 100] |
<100 |
|
49-54 |
特定字元的出現頻率 |
[0, 100] |
<100 |
|
55 |
大寫字母遊程均長 |
[1, …] |
1102.5 |
|
56 |
最長大寫字母遊程 |
[1, …] |
9989 |
|
57 |
大寫字母遊程總長 |
[1, …] |
15841 |
|
58 |
垃圾郵件標識(1代表垃圾郵件) |
{0, 1} |
1 |
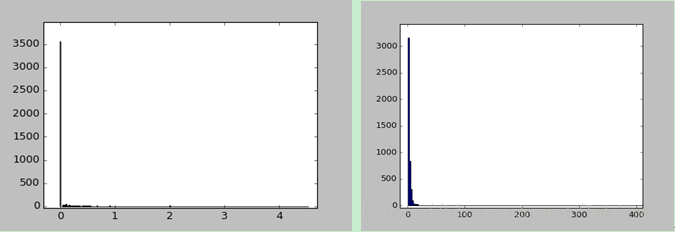
第1-54屬性可以看成統計特性相似的一類,因為它們都代表了單詞或字元的出現頻率,範圍都是[0, 100]. 考察第1個屬性的分佈規律,對全部4601個樣本做頻數統計,如圖2-1(a), 可見大部分樣本的值為0,還有少部分分佈在1以內,均值在零點幾左右。
同樣,第55~57個屬性的統計特性應當是一致的,都表示遊程的長度。對第55個屬性的數值作頻數統計,如圖2-1(b), 雖然數值的分佈範圍很大,但主要集中分佈在數值較小的區域。
圖 22 (a)屬性1的數值分佈, (b)屬性55的數值分佈
顯然,這樣的分佈不能用高斯分佈或其他分佈函式來表示。所以可以建立離散的概率密度函式,用樣本的頻數估計概率密度。
頻數統計首先確定組距,或者稱之為量化階:
\[Quantization\_order = \frac{{Max - Min}}{{Bins}}\]
其中,Max是可接受資料的最大值,min是最小值,Bins為組數。
然後建立頻數表,其長度就是組數Bins。遍歷待統計的資料,判斷每個資料落入何組中,頻數表中對於的數值就加1.
如果要得到概率,只需將頻數除以總樣本數。
貝葉斯分類器
原理:
貝葉斯分類是一種有監督的分類方法。其原理如下:首先統計各類的先驗概率,以及類條件概率分佈,然後通過貝葉斯公式:
\(P({\omega _i}|{\mathbf{x}}) = \frac{{P({\mathbf{x}}|{\omega _i}) \cdot P({\omega _i})}}{{P({\mathbf{x}})}} = \frac{{p({\mathbf{x}}|{\omega _i})d{\mathbf{x}} \cdot P({\omega _i})}}{{p({\mathbf{x}})d{\mathbf{x}}}} = \frac{{p({\mathbf{x}}|{\omega _i}) \cdot P({\omega _i})}}{{p({\mathbf{x}})}}\)( 1)
可以利用已知量轉換得到後驗概率 \(P({\omega _i}|{\bf{x}})\),即表示在特徵x時屬於類\({\omega _i}\) 的概率分佈。
從式(1)還可以看出,因為 \(P({\bf{x}}|{\omega _i})\)=\(p({\bf{x}}|{\omega _i})d{\bf{x}}\),分子分母同時消去後,後驗概率分佈實際上也可以通過先驗概率密度來計算。而且實際上,\(p({\bf{x}}|{\omega _i})\) 比\(P({\bf{x}}|{\omega _i})\)更容易表示,所以一般使用\(p({\bf{x}}|{\omega _i})\)計算後驗概率。
樸素貝葉斯
如果樣本的特徵向量x維數很大,會給條件概率密度函式\(p({\bf{x}}|{\omega _i})\)的求取帶來困難。假設各屬性的值相互獨立,則\(p({\bf{x}}|{\omega _i})\)可以表示為:
$$p({\bf{x}}|{\omega _i}) = \prod p({x_k}|{\omega _i})$$(2)
將式(2)代入式(1),就得到了樸素貝葉斯的表示式:
$$P({\omega _i}|{\bf{x}}) = \frac{{\prod p({x_k}|{\omega _i}) \cdot P({\omega _i})}}{{p({\bf{x}})}} = $$(3)
而\(\prod p({x_k}|{\omega _i})\)中的每一項,可以使用第2節中所說的頻數進行估計。
決策規則
對於兩類分類問題,根據後驗概率的大小判決所屬分類,即:

基於上式,代入貝葉斯公式,由於分母都一樣,可以得到變換形式的決策式:
 (4-a)
(4-a)
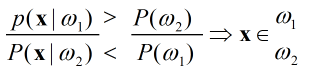 (4-b)
(4-b)
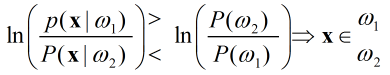 (4-c)
(4-c)
他們都是等價的,針對不同的後驗概率形式,選擇最簡單的表示式即可。在本題中,使用4-a更方便。
程式設計
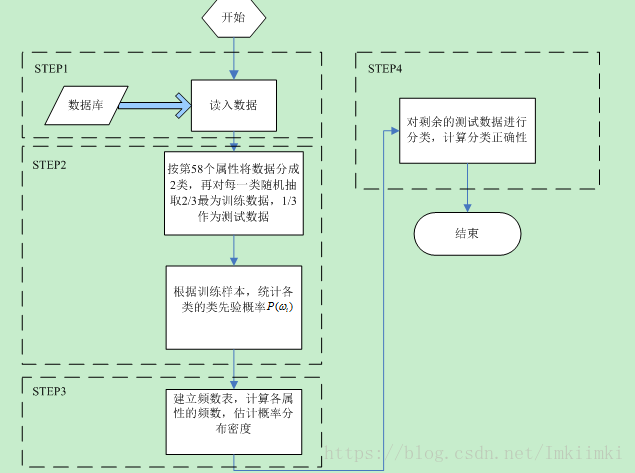
通過上述原理的分析,該題的主要計算工作可以分為4步,用順序結構即可實現。框圖歸納如下:
圖 41程式流程圖
圖中標註的步驟編號與程式原始碼中的註釋相對應。
程式設計實現
程式按照框圖中的4個主要步驟設計。為了將更清楚地顯示執行過程,在相同目錄下建立了一個文字檔案Tracking.log,每一個Step執行完成後,使用file.write()函式在檔案中寫入執行時間戳和執行結果。
建立文字檔案的程式碼如下,使用寫入模式w,若不存在則建立,若已存在同名檔案,會清空內容後重新建立。
file= open('Tracking.log','w',buffering=100)#建立一個檔案,用於寫入執行報告Step1讀入資料,並統計長度
spambase.data中的資料一行有58個,用","分隔。使用numpy的loadtxt()函式可以直接讀入,返回一個array物件屬性。然後使用array.shape方法得到資料的維度。
original_data_readin = np.loadtxt("spambase.data", dtype=float, delimiter=",")
size = original_data_readin.shape
sampleNums_of_classALl = size[0];#樣本總數
sampleNums_of_class_spam=int(sum(original_data_readin[:,-1]))#統計屬於垃圾郵件的樣本數量(1813)
sampleNums_of_class_good= sampleNums_of_classALl - sampleNums_of_class_spam #正常郵件的數量
length_of_attributes = size[1];#屬性向量的長度(應該是58)程式執行後,original_data_readin變數中儲存了讀取的原始資料, sampleNums_of_classALl是所有樣本的數量,sampleNums_of_class_spam是垃圾郵件樣本數量,sampleNums_of_class_good是正常郵件的樣本數量,length_of_attributes是特徵屬性長度。
Step2隨機產2/3的資料用於訓練,並計算類先驗概率
這一部分位於原始碼的line49-70.
所給的資料庫中,垃圾郵件和非垃圾郵件已經分類,前面是垃圾郵件,後面是非垃圾郵件。以垃圾郵件中產生2/3訓練樣本為例,說明隨機抽取的方法:
遍歷所有垃圾郵件樣本,使用random.uniform(0,3)函式產生0-3均勻分佈的隨機數,與1比較,如果小於1,歸類為測試樣本;大於等於1,則歸類為訓練樣本。將垃圾郵件的訓練樣本存入矩陣sampls_spam_train,測試樣本存入sampls_spam_test.
同理,對正常郵件也進行2/3隨機抽取,訓練樣本存入矩陣sampls_good_train,測試樣本存入sampls_good_test.
隨後,根據sampls_spam_train和sampls_good_train的長度,計算了類先驗概率和.
檔案Tracing.log中寫入這一步的執行結果。
Step3 根據頻數估計類條件概率
如第二節中所述,使用頻數估計類條件概率密度。這裡定義了一個函式:Hist_Estimate(data,bins, min,max,normal),具體如下:
def Hist_Estimate(data=np.zeros((1,54)),bins=quant_order, min=0.0,max=100,normal=1 ):
#@對輸入的資料進行頻數估計,返回bins×data.shape[1]維的向量
deltaX=float(bins)/(max-min)
#print deltaX
pdf=np.zeros((bins,data.shape[1]))
for i in range(data.shape[1]):#pdf的列遍歷
#print i
for j in range (data.shape[0]):#統計頻數
#print str(i)+str(j)
pdf[int(deltaX*data[j,i]),i] += 1
if normal!=1: #返回不歸一化的頻數
return pdf
else: #返回歸一化的頻數,可以看作概率密度函式
return pdf/data.shape[0]
它實現了第2節中所述的頻數統計功能,輸入data是N*n的樣本(N為樣本數,n為特徵數),bins量化階數,min和max分別表示頻數表的最小和最大值,normal=1返回歸一化的頻率,否則返回頻數。返回值是一個bins*n的矩陣,每一列就是一個屬性的頻數(或頻率)表。由於樣本中前54個屬性的值範圍為[0,100],而55,56,57三個屬性的值從1到幾千,所以使用對他們分兩種情況求頻數。呼叫Hist_Estimate()函式時,前者取min=0, max=100,後者的min=1, max=20000. 量化階bins都取同樣值,這樣返回的頻數表長度都是一樣的。
pdf54_spam = Hist_Estimate(sampls_spam_train[:,:54],bins=quant_order)
pdf54_good = Hist_Estimate(sampls_good_train[:,:54],bins=quant_order)
pdf57_spam = Hist_Estimate(sampls_spam_train[:,54:57],min=0.0,max=20000,bins=quant_order)
pdf57_good = Hist_Estimate(sampls_good_train[:,54:57],min=0.0,max=20000,bins=quant_order)pdf54_spam中儲存了垃圾郵件類中前54個屬性的頻數表,pdf57_spam是後3個屬性的頻數表。非垃圾郵件也類似處理。
這部分的程式碼在line 84 – 103.
Step4 使用測試集資料對分類器作效能測試
通過之前的步驟,已經得到了類先驗概率和類條件概率密度.由式(3)可以計算出後驗概率,再根據式(4-a)做出決策。
函式Gx_Compute(data,px,bins, min,max)用於計算一個輸入樣本的各個屬性的先驗概率乘積,即. 由於有些值的概率密度為0,為了避免乘0後結果恆為0,加上了一個微小的常數0.001,所以實際上計算的是.函式Gx_Compute()的輸入引數data是一個樣本中某些屬性組成的向量(1*nk),px是對於的頻率表(bins*nk), bin是量化階數,min和max是頻率表中的最小值和最大值。
首先測試垃圾郵件的分類效能。呼叫函式Gx_Compute(),對sampls_spam_test中的一個樣本,計算式(4-a)左右兩項。由於57個屬性分成了兩種量化階不同的統計,所以計算需要使用兩次Gx_Compute(),計算也需要使用兩次Gx_Compute(). 比較和的值,如果前者大,則判為垃圾郵件,即正確分類了,計數值amount_of_test_spam_correct加一。遍歷完所有待測試垃圾郵件之後,計算正確識別的比例,即amount_of_test_spam_correct / amount_of_test_spam_total.垃圾郵件分類測試的程式碼如下:
#對spam測試樣本進行檢驗
amount_of_test_spam_total = sampls_spam_test.shape[0]
amount_of_test_spam_correct = 0
for i in range(amount_of_test_spam_total):
if (Gx_Compute(sampls_spam_test[i,0:54],pdf54_spam)*Gx_Compute(sampls_spam_test[i,54:57],pdf57_spam,quant_order,0.0,20000)*Pw1>Gx_Compute(sampls_spam_test[i,0:54],pdf54_good)*Gx_Compute(sampls_spam_test[i,54:57],pdf57_good,quant_order,0.0,20000)*Pw2 ):
amount_of_test_spam_correct +=1
print u'垃圾郵件正確檢出率'
print float(amount_of_test_spam_correct) / amount_of_test_spam_total
檢驗正常郵件識別效能的方法與之相同,只是改變了輸入樣本,並反轉判決條件。
這部分的程式碼位於line 124 – 145, 檢測結果會列印在螢幕上,同時寫入日誌。
執行結果
使用pyinstaller工具打包編譯成了單檔案exe,將資料檔案和程式放在同一目錄下,執行exe。
圖 61資料檔案和編譯得到的程式
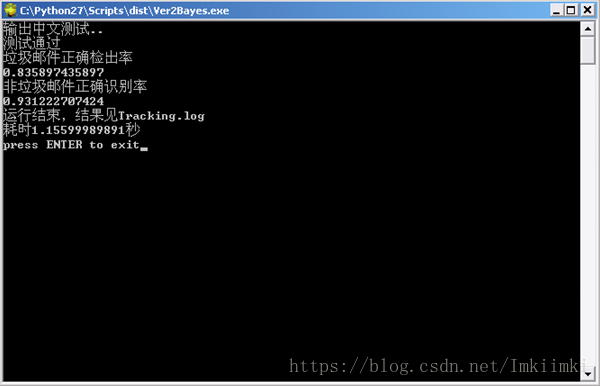
圖 62 執行結果
等待程式將所需的動態連結庫解壓到系統快取後,就會執行python程式,本次執行,垃圾郵件檢出率在0.83,正常郵件識別率在0.93,運行了大約1.15秒。開啟目錄下生成的Tracking.log文字檔案,如下所示:
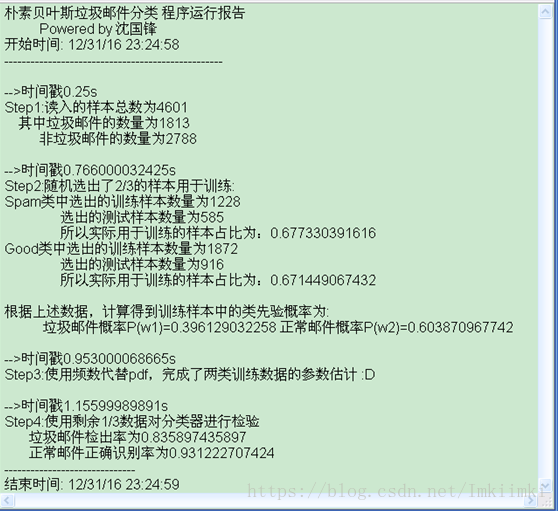
圖 63 log檔案
檔案中記錄了每步完成的時間,也記錄了關鍵步驟的運算結果。從結果來看,程式功能是正確的。
總結
本次的程式設計過程比較順利,寫完一個步驟就進行驗證,沒有出現找很久Bug的情況。由於不涉及複雜矩陣運算,幾乎所有的運算操作都是從0開始自己寫的,沒有使用別的庫,也就沒有參考程式。但這直接造成了程式冗長繁雜,寫的有些隨意,有些計算方法也不是最優的。幸好我認為變數定義還是很清楚的,看到名稱可以大概想到其含義,否則就真的寫完之後我自己也看不懂了。
在一開始寫的時候,我感覺訓練好分類器,然後檢測一下分類結果,輸出一個正確率,程式就結束了,似乎不是很直觀,而且編寫時也正好需要除錯,突發奇想就想把關鍵步驟的執行結果寫到文字檔案裡。後來又加了一個毫秒精度的時間戳,這樣每一步執行了多少時間,都會寫到日誌裡,這就很有意思了,看到日誌似乎可以回顧程式的執行過程。
這次還使用了pyinstaller工具,將python程式編譯成了exe,這樣即使在沒有安裝python的計算機上也可以執行。
此外,還遇到了一些問題。首先是print語句列印中文亂碼問題,表現為在IDLE的shell中是正常的,但在控制檯中執行就會亂碼。最後查詢到原因是系統的編碼與py2.7不同。這在python3中已經解決,但對於python2,需要對編碼進行轉換:
import sys
type = sys.getfilesystemencoding()
print '輸出中文測試..'.decode('utf-8').encode(type)
或者在字元前加u,表示unicode編碼:
print u'中文測試'
對於概率密度的計算,使用了頻數進行估計。這就涉及到量化階的問題,即把多大的範圍看作一個頻數統計區間。如果把量化階取得過大,一些原本有差異的數值會落入同一個統計區間中,這樣就使得模型的靈敏度降低,影響分類效果;但是如果量化階取得過小,即頻數分組很多,在有限的訓練樣本下,就會造成估計的失準,最後也影響分類準確率。程式中使用了500個量化值進行統計,效果較好。
取不同的頻數量化組數,識別率變化如下,說明量化組數在200到1000內比較理想。
|
頻數量化組數 |
垃圾郵件識別率 |
非垃圾郵件正確識別率 |
|
100 |
0.835820895522 |
0.891832229581 |
|
200 |
0.85641025641 |
0.929399367756 |
|
500 |
0.855687606112 |
0.949506037322 |
|
1000 |
0.809825673534 |
0.953241232731 |
|
1500 |
0.786991869919 |
0.93237704918 |
|
2000 |
0.802931596091 |
0.932584269663 |
|
3000 |
0.78813559322 |
0.924528301887 |
此外,垃圾郵件的識別率總是比正常郵件的識別率低,我就想到一句話:正常郵件都是相似的,垃圾郵件各有各的不同。
好了,寫到這裡正好跨年了,我就回去把第一頁的日期也改了,祝大家新年快樂!