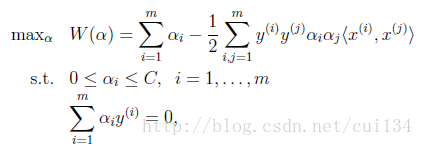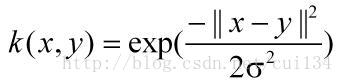python機器學習之SMO演算法
SVM演算法計算到後面是一個帶約束條件的優化問題
這裡的SMO(Sequential Minimal Optimization)序列最小化演算法就是一個二次規劃優化演算法,可以用來解決上面的問題。SMO演算法是由John C.Platt在1998年提出的。SMO演算法的目標就是求出一些列的alpha和b,一旦求出這些alpha,就可以計算出權重向量,並求出分割超平面。SMO演算法的工作原理是:每次迴圈中選擇兩個alpha進行優化處理。一旦找到一對合適的alpha,那麼就增大其中一個,同時減少另一個。那麼為什麼每次都要選擇兩個alpha進行優化呢,我們可以看到以上公式中有一個約束條件:
因此,如果只改變其中一個alpha,那麼這個約束條件就無法滿足,因此需要選擇2個alpha同時進行優化,並且增大其中一個,另一個也要減小相同的大小。這裡選擇alpha的方式採用啟發方式,具體步驟:先通過外迴圈來選擇第一個alpha,選擇過程會在兩種方式下交替:一種方式是在所有資料集上進行單遍掃描,另一種是在非邊界alpha中實現單遍掃描,這裡的非邊界alpha是指大於0小於C的alpha的值,這裡的C是自己設定的,之後,在選擇完第一個alpha後,演算法會通過一個內迴圈來選擇第二個alpha,通過最大步長的方式來選擇第二個alpha,假設Ej是Xj的估計值與實際值的誤差,j是第二個alpha的編號,i是第一個alpha的編號,那麼則選取Ei-Ej最大的那個alpha來作為第二個優化的值。
程式碼如下:
首先,定義一個類:
class optStruct: def __init__(self,dataMatIn, classLabels, C, toler): # 建構函式 self.X = dataMatIn self.labelMat = classLabels self.C = C self.tol = toler self.m = shape(dataMatIn)[0] self.alphas = mat(zeros((self.m,1))) self.b = 0 self.eCache = mat(zeros((self.m,2))) #用於儲存誤差E
<span style="white-space:pre"> </span>self.K = mat(zeros((self.m,self.m)))#計算向量經過核函式的值
for i in range(self.m):
self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
def calcEk(oS, k):#返回計算的誤差 fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b) Ek = fXk - float(oS.labelMat[k]) return Ek def selectJ(i, oS, Ei):#啟發方式選擇第二個alpha maxK = -1; maxDeltaE = 0; Ej = 0 oS.eCache[i] = [1,Ei] validEcacheList = nonzero(oS.eCache[:,0].A)[0] if (len(validEcacheList)) > 1: for k in validEcacheList: #選擇Ei-Ej最大的alpha if k == i: continue Ek = calcEk(oS, k) deltaE = abs(Ei - Ek) if (deltaE > maxDeltaE): maxK = k; maxDeltaE = deltaE; Ej = Ek return maxK, Ej else: #第一次計算的時候,eCache為0 j = selectJrand(i, oS.m)#隨機選擇 Ej = calcEk(oS, j) return j, Ej
def updateEk(oS, k):#更新Ek
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
def innerL(i, oS):#內迴圈
Ei = calcEk(oS, i)
#滿足該條件,進行優化
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i, oS, Ei) #選擇j
alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H: print "L==H"; return 0
eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #用於後續更新alpha
if eta >= 0: print "eta>=0"; return 0
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
updateEk(oS, j) #更新j的誤差
if (abs(oS.alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])
updateEk(oS, i) #更新i的誤差
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else: return 0
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #外迴圈
oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
iter = 0
entireSet = True; alphaPairsChanged = 0#非0表示alpha經過優化
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: #遍歷所有值
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS)
print "fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)
iter += 1
else:#遍歷非邊界值
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print "non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)
iter += 1
if entireSet: entireSet = False #遍歷完所有值
elif (alphaPairsChanged == 0): entireSet = True
print "iteration number: %d" % iter
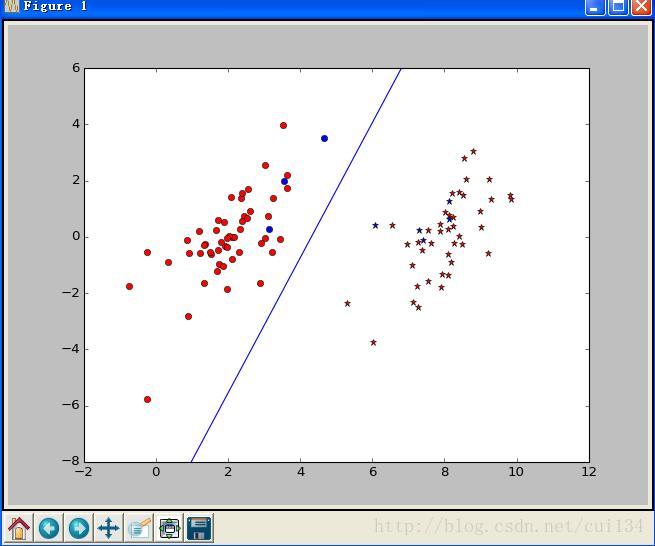
return oS.b,oS.alphas訓練結果如下:
藍色點代表支援向量,w矩陣就是由這些支援向量計算來的,因此,在訓練完成後,可以通過支援向量來對未知向量進行分類。
對於複雜的資料而言,有些資料是不能夠像上圖一樣能夠線性可分的。
因此,我們可以把訓練資料對映到一個高維的空間去,也許在這個高維空間,可以線性可分。這裡實際上就是對向量進行一個變換。但是我們不需要把向量變換到高維之後在進行內積,因為根據泛函的有關理論,只要一種核函式K(xi,yi)滿足Mercer條件,它就對應某一變換空間中的內積。
這裡介紹一個常用的核函式,徑向基核函式:
程式碼如下:
def kernelTrans(X, A, kTup): #核函式計算
m,n = shape(X)
K = mat(zeros((m,1)))
if kTup[0]=='lin': K = X * A.T #線性核函式
elif kTup[0]=='rbf':
for j in range(m):
deltaRow = X[j,:] - A
K[j] = deltaRow*deltaRow.T
K = exp(K/(-1*kTup[1]**2)) #計算經過核函式計算後的值
else: raise NameError('Houston We Have a Problem -- \
That Kernel is not recognized')
return K下面利用徑向基核函式對上圖進行分類
def testRbf(k1=1.3):
dataArr,labelArr = loadDataSet('testSetRBF.txt')
for i in range(100):
if labelArr[i]==1:
pl.plot(dataArr[i][0],dataArr[i][1],'b*')
else:
pl.plot(dataArr[i][0],dataArr[i][1],'bo')
pl.xlim([-1.5,1.5])
pl.ylim([-1.5,1.5])
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd] #得到支援向量的點
labelSV = labelMat[svInd];
print "there are %d Support Vectors" % shape(sVs)[0]
m,n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print "the training error rate is: %f" % (float(errorCount)/m)
dataArr,labelArr = loadDataSet('testSetRBF2.txt')
errorCount = 0
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
m,n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)==1:
pl.plot(dataArr[i][0],dataArr[i][1],'r*')
else:
pl.plot(dataArr[i][0],dataArr[i][1],'ro')
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print "the test error rate is: %f" % (float(errorCount)/m)
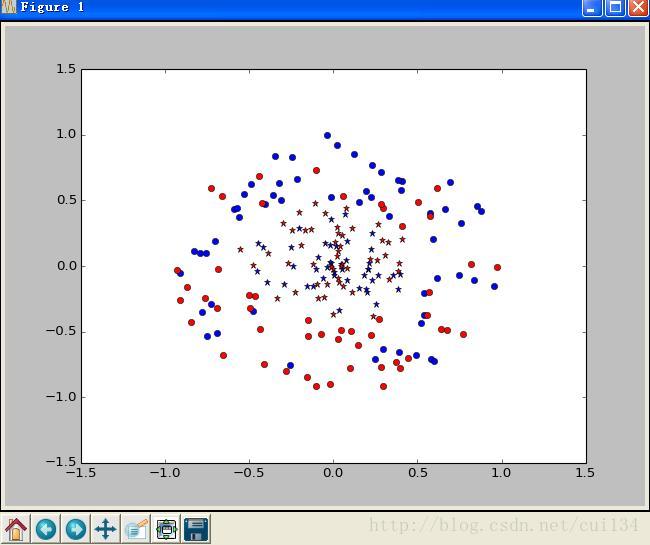
pl.show()結果
如圖,藍色是訓練資料,紅色是測試資料,可以看出,經過藍色資料的訓練之後,儘管測試資料不是線性可分,SVM仍可以對測試資料很好的分類。