在電腦科學中，並查集是一種樹型的資料結構，用於處理一些不交集（Disjoint Sets）的合併及查詢問題。有一個聯合-查詢演算法（union-find algorithm）定義了兩個用於此資料結構的操作：

• Find：確定元素屬於哪一個子集。它可以被用來確定兩個元素是否屬於同一子集。
• Union：將兩個子集合併成同一個集合

問題:

假如已知有n個人和m對好友關係（存於數字r）。如果兩個人是直接或間接的好友（好友的好友的好友…），則認為他們屬於同一個朋友圈，請寫程式求出這n個人裡一共有多少個朋友圈。假如：n = 5，m = 3，r = {{1 , 2} , {2 , 3} , {4 , 5}}，表示有5個人，1和2是好友，2和3是好友，4和5是好友，則1、2、3屬於一個朋友圈，4、5屬於另一個朋友圈，結果為2個朋友圈。

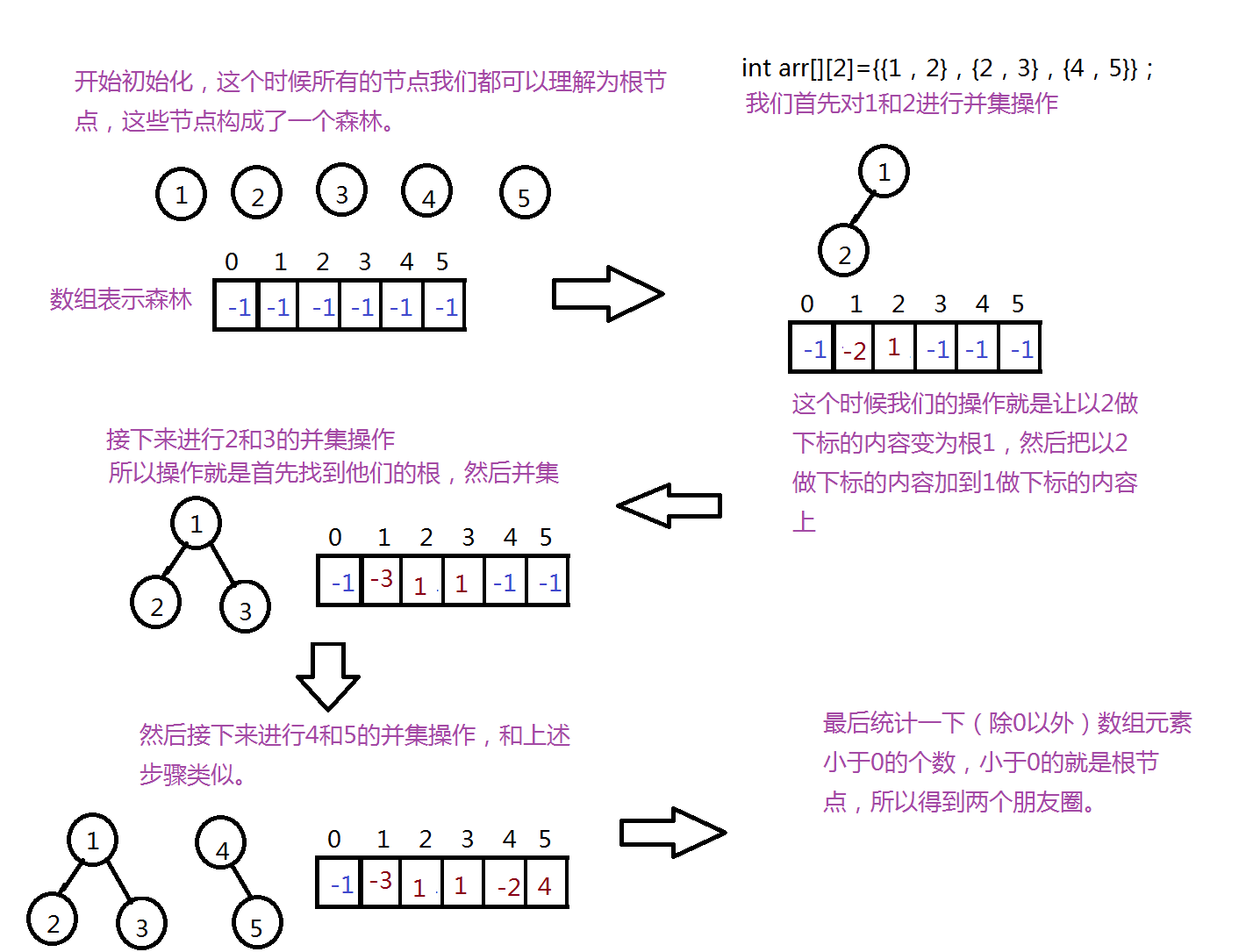
並查集森林是一種將每一個集合以樹表示的資料結構，其中每一個節點儲存著到它的父節點的引用，例如對於本題目

並查集的實現可以理解成森林。每一個下標對應是是一棵樹。在這裡我們用可以用一個數組來表示這個森林，而根節點的內容我們認為都是-1。所以，預設的整個陣列數值都為-1。即初始化為：

具體實現過程:

實現程式碼:

#pragma once
#include<iostream>
#include<vector>
using namespace std;

class UnionSet {
public:
	UnionSet(int n)
	{
		_v.resize(n + 1, -1);
	}
	//n個人 m對關係  
	int Find(int index)
	{
		int root = index;

		while (_v[root]>=0)
		{
			root = _v[root];
		}
	
		return root;
	}

	void Merge(int n,int m, int r[][2])
	{
		for (int i = 0; i < m; i++)//合併兩個集合  
		{
			//找到真正的根 對根操作
			int root1 = Find(r[i][0]);
			int root2 = Find(r[i][1]);

			if (root1 != root2)
			{
				//合併兩個集合
				_v[root1] += _v[root2];
				_v[root2] = root1;
			}
			
		}
	
	}
	int CountSet()
	{
		int count = 0;
		for (size_t i = 1; i < _v.size(); i++)
		{
			if (_v[i] < 0)
				count++;
		}
		return count;
	}
private:
	vector<int> _v;
};
void TestUnionSet()
{
	
	int n = 5;
	int m = 3;
	int r[][2] = { {2,1},{3,2},{4,5 } };
	UnionSet u(n);
	u.Merge(n, m, r);
	int count = u.CountSet();
	cout << count << endl;
	int i = 0;
}