並查集(Union-Find)演算法詳解
並查集(Union-Find)是解決動態連通性問題的一類非常高效的資料結構。本文中,我將盡我所能用最簡單,最清晰的邏輯展示出並查集的構造過程,同時還將對其中的關鍵步驟給出相應的Python程式碼。
動態連通性
可以想象一張地圖上有很多點,有些點之間是有道路相互聯通的,而有些點則沒有。如果我們現在要從點A走向點B,那麼一個關鍵的問題就是判斷我們能否從A走到B呢?換句話說,A和B是否是連通的。這是動態連通性最基本的訴求。現在給出一組資料,其中每個元素都是一對“點”,代表這對點之間是聯通的,我們需要設計一個演算法,讓計算機依次讀取這些資料,最後判斷出其中任意兩點是否連通。注意,並查集所涉及的動態連通性只是考慮“是否連通”這一二值判別問題,而不涉及連通的路徑到底是什麼。後者不在本文的考慮範圍之內。
舉個例子,比如下圖。為了簡單起見,我們以整數 0~9 表示圖中的10個點,然後給出兩兩連通的資料如下:[(4, 3), (3, 8), (6, 5), (9, 4), (2, 1), (8, 9), (5, 0), (7, 2), (6, 1), (6, 7)]
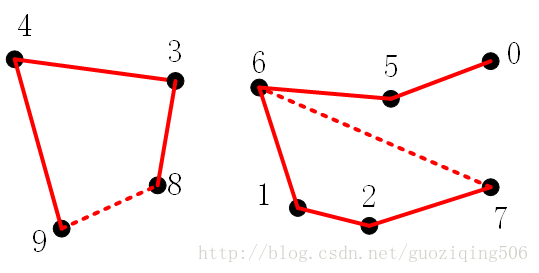
我們將這些“點對”依次通過畫圖連線的方式在圖中表示出來。當然,如果其中某“對”點本身就是連通的,比如點對
為了實現上面所描述的功能,一個簡單的思路就是分組。也就是說,我們可以把相互連通的點看成一個組,如果現在查詢的點對分別在不同的組中,則這個點對不連通,否則連通。下面我們先來簡單分析一下這種操作的具體過程,分“並”和“查”兩個方面來分析。為了方便描述,我這裡先舉一個例子:比如上圖的10個點,現在就令每個點的值為其初始組別,我們可以得到下面這個表:
| element | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| group number | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
現在,“並”的操作可以這樣來描述:觀察第一個點對
| element | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| group number | 0 | 1 | 2 | 3 | 3 | 5 | 6 | 7 | 8 | 9 |
而“查”的操作其實就是“並”操作的第一步:找到點對中兩個點所在的組別,看是否相同。
也就是說,並查集的兩類基本操作中,都涉及了“根據點找組別”的過程,因此我們先給出一個高效的“查”的演算法。我把它叫做Quick-Find 演算法。
Quick-Find 演算法
設計高效的查詢演算法非常簡單,從上面的表格我們就能聯想到,這種元素和組別之間的一一對應關係可以用“鍵值對”的儲存方式實現。我直接給出Python的實現程式碼,非常簡單。
def con_eleGroupNum(eleList):
"""
construct the element-group number map
:param eleList: the list of distinct elements
:return: the dictionary with the form {element: group number}
"""
result = {}
num = 1
for i in eleList:
result[i] = num
num += 1
return result這樣,因為可以直接找到“鍵”,並通過“鍵”訪問其對應的值,所以查詢的複雜度為
但是如果是並呢?這就有點麻煩了,因為不知道到底是哪些“鍵”(點)對應著某個“值”(組別),所以需要對整個列表進行遍歷,逐一修改。假設現在有
def change_GroupNum(pairGroupNum, eleGroupNum):
"""
connect
:param pairGroupNum: the two group numbers of the pair of elements
:param eleGroupNum: the dictionary with the form {element: group number}
:return: None
"""
newGroupNum = min(pairGroupNum)
for i in eleGroupNum:
if eleGroupNum[i] == pairGroupNum[0] or eleGroupNum[i] == pairGroupNum[1]:
eleGroupNum[i] = newGroupNum
def quick_find(elePair, eleGroupNum):
"""
find and connect
:param elePair: the pair of elements
:param eleGroupNum: the dictionary
:return: None
"""
pairGroupNum = (eleGroupNum[elePair[0]], eleGroupNum[elePair[1]])
change_GroupNum(pairGroupNum, eleGroupNum)Quick-Union 演算法
為了解決這種低效的並,我們需要重新考慮一下這個問題。現在的關鍵在於如何能快速地通過一個點找到其相應的組別和這個組中的所有點,並且批量改變這些點的組別。顯然,這裡面設計了資料的儲存和更新,我們考慮從設計新的資料結構入手。既然簡單的鍵值對無法解決,那麼別的資料結構呢?連結串列,樹,圖?琢磨一下,你會發現樹結構其實很適合:比起連結串列和圖,樹結構有一個非常“顯眼”的根節點,我們可以用它來代表這個樹所有節點的組別,修改了根節點,就相當於是修改了全樹,此外,樹的層次化結構決定了由一個節點查詢到組別的過程也是非常高效的。
用樹結構實現並查集的演算法思路可以如下描述,假設現在要新增多個路徑(點對):
初始化:每個點看做一棵樹,當然這是一棵只有根節點的樹,儲存了這個節點本身的值作為組別(你也可以令其他不會產生衝突的記號做組別);
查詢:對於點對
(a,b) ,通過a 和b 向其根節點回溯(當然初始時就是它們本身),判斷其所在組別;合併:若不在同一組別,令其中一個點(比如
a 吧)所在樹的根節點成為另一個點(比如b )的根節點的孩子。這樣即便再查詢到a ,通過上面的查詢過程,程式也會最終判斷得到的是現在b 的根節點所在的組別,相當於是改變了a 所在組的全部元素的組別;
這樣,在計算過程中的所有樹其實就是一棵多叉樹。然而我們發現,現在產生了一個新的問題,那就是因為查詢演算法也改了,導致現在Quick-Union的查詢過程效率好像不那麼令人滿意了。甚至在最壞的情況下,這樣的多叉樹退化成了一個連結串列(不具體說了,大家想想應該能明白)。
但是沒辦法啊,因為你要找樹根,怎麼著複雜度也得是
大樹小樹的合併技巧
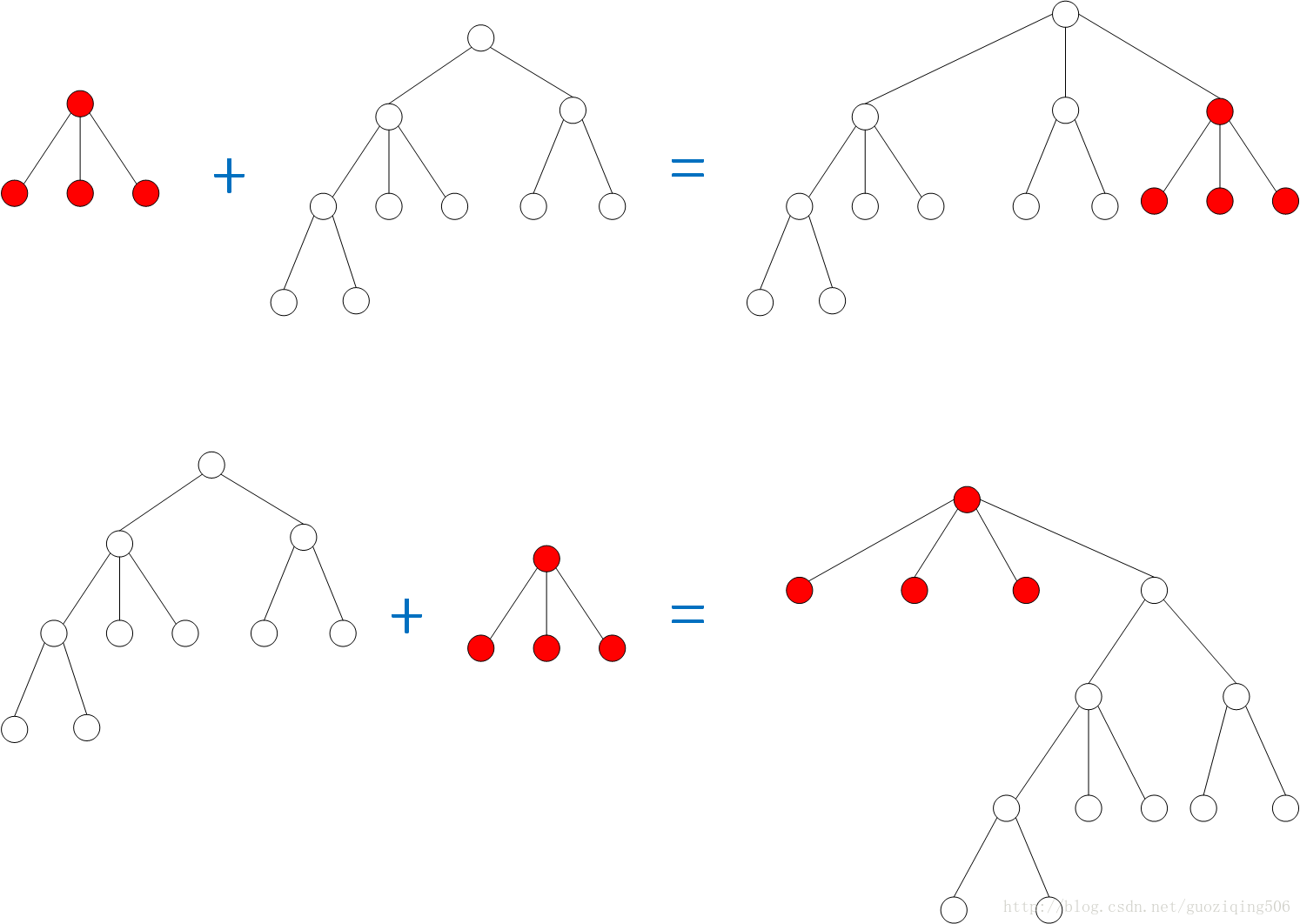
先看看樹的合併,對於我們上面說的這種合併(一棵樹的根直接變成另一棵樹根的孩子),有一個基本的原則是小樹變成大樹的子樹,會比大樹變成小樹的子樹更加不易增加樹高,這一點通過下面的圖就能看出來。所以我們可以在生成樹的時候,令根節點儲存一個屬性 weight,用來表示這棵樹所擁有的節點數,節點數多的是“大樹”,少的就是“小樹”。
壓縮路徑
再看看樹的生成,這一點就要在查詢過程中做文章了,因為每次我們是從樹的一個節點回溯到其根節點,所以一個最直接的辦法是,將這條路徑上的所有中間節點記錄下來,全部變成根節點的子節點。但是這樣一來會增加演算法的空間複雜度(反覆開闢記憶體和銷燬)。所以一個備選的思路是每遍歷到一個節點,就將這個節點變成他的爺爺節點的孩子(和其父節點在同一層了)。相當於是壓縮了查詢的路徑,這樣,頻繁的查詢當然會導致樹的“扁平化”程度更徹底。
程式碼展示
經過上面大小樹的合併原則以及路徑的壓縮,其實“並”和“查”兩種操作的時間複雜度都非常趨近於
class UFTreeNode(object):
def __init__(self, num):
# the group number
self.num = num
# its children
self.children = []
# its parent
self.parent = None
# the number of nodes that rooted by this node
self.weight = 1
def genNodeList(eleList):
"""
generating the node of each element
:param eleList: the list of elements
:return: a dictionary formed as {element: corresponding node}
"""
result = {}
for ele in eleList:
result[ele] = UFTreeNode(ele)
return result
def locPair(elePair, eleNodeMap):
"""
locate the positions of the pair of elements
:param elePair:
:param eleNodeMap: a dictionary formed as {element: corresponding node}
:return: the two nodes of the pair of elements
"""
return [eleNodeMap[elePair[0]], eleNodeMap[elePair[1]]]
def backtracking(node):
"""
1. find the root of a node
2. cut down the height of the tree
:param node:
:return: the root of node
"""
root = node
while root.parent:
cur = root
root = root.parent
# the grandfather node of cur exists
if cur.parent.parent:
# make the father of cur is its grandfather
grandfather = cur.parent.parent
grandfather.children.append(cur)
return root
def quickUnion(elePair, eleNodeMap):
"""
union process
:param elePair:
:param eleNodeMap:
:return:
"""
nodePair = locPair(elePair, eleNodeMap)
root_1, root_2 = backtracking(nodePair[0]), backtracking(nodePair[1])
# if the two elements of the pair are not belongs to the same root (group)
if root_1 is not root_2:
if root_1.weight >= root_2.weight:
# update weight
root_1.weight += root_2.weight
# make the root2 as a subtree of root1
root_1.children.append(root_2)
# update the group number of root2
root_2.num = root_1.num
else:
root_2.weight += root_1.weight
root_2.children.append(root_1)
root_1.num = root_2.num相關推薦
並查集(Union-Find)演算法詳解
並查集(Union-Find)是解決動態連通性問題的一類非常高效的資料結構。本文中,我將盡我所能用最簡單,最清晰的邏輯展示出並查集的構造過程,同時還將對其中的關鍵步驟給出相應的Python程式碼。 動態連通性 可以想象一張地圖上有很多點,有些點之間是有道
並查集(Union-Find)演算法
本文轉載自csdn另一博主,其原文點這裡。 public int find(int[] parent, int i) { if (parent[i] != i) { parent[i] = find(parent, pare
資料結構與演算法(十二)並查集(Union Find)
本文主要包括以下內容: 並查集的概念 並查集的操作 並查集的實現和優化 Quick Find Quick Union 基於size的優化 基於rank的優化 路徑壓縮優化 並查集的時間複雜度 並查集的概念 在電腦科學中,並查集 是一種樹形的資料結
演算法入門---java語言實現的並查集(Union-Find)小結
圖片來自慕課網,僅僅為了記錄學習。 基本概念 /** * * 並查集,用來解決連通問題的,兩個節點之間是否是連通的。 * 此處的節點是抽象的概念:比如使用者和使用者之間,港口和港口之間。
POJ 1611 The Suspects 並查集 Union Find
subset oid fin 由於 urn data tracking -m cts 本題也是個標準的並查集題解。 操作完並查集之後,就是要找和0節點在同一個集合的元素有多少。 註意這個操作,須要先找到0的父母節點。然後查找有多少個節點的額父母節點和0的父母節點同樣。
並查集(Union-Find)
數組 樹根 情況 由於 指針 oid 父節點 要求 基本 一、基本操作: 1、Find:當且僅當兩個元素屬於相同的集合時,返回相同的名字 2、Union:將兩個不相交的集合合並為一個不想交的集合。 應用:在等價關系中,判斷兩個元素之間是否有關系或者添加等價關系。 二、基本數
【LeetCode】並查集 union-find(共16題)
p.p1 { margin: 0.0px 0.0px 0.0px 0.0px; font: 12.0px Helvetica } 【128】Longest Consecutive Sequence 【130】Surrounded Regions 【200】Number of Is
資料結構——並查集Union Find
一、並查集解決了什麼問題? 1、網路中節點間的連線狀態:這裡的網路是一個抽象的概念,指的是使用者之間形成的網路 2、兩個或兩個以上集合之間的交集 二、對並查集的設計 對於一組資料,主要支援兩個操作 public interface UnionFind {
並查集(Union-Find Sets)及其應用
並查集 (Union-Find Sets)並查集:(union-find sets)是一種簡單的用途廣泛的集合. 並查集是若干個不相交集合,能夠實現較快的合併和判斷元素所在集合的操作,應用很多。一般採取樹形結構來儲存並查集,並利用一個rank陣列來儲存集合的深度下界,在查詢操
並查集(Union-Find) 應用舉例
本文是作為上一篇文章 《並查集演算法原理和改進》 的後續,焦點主要集中在一些並查集的應用上。材料主要是取自POJ,HDOJ上的一些演算法練習題。 首先還是回顧和總結一下關於並查集的幾個關鍵點: 以樹作為節點的組織結構,結構的形態很是否採取優化策略有很大關係,未進行優化的樹結構可能會是“畸形”樹(嚴重不
並查集(Union-Find)粗略介紹
並查集:一種樹型的資料結構,用於處理一些不相交集合(Disjoint Sets)的合併及查詢問題。常常在使用中以森林來表示。 集:就是讓每個元素構成一個單元素的集合,也就是按一定順序將屬於同一組的元素所在的集合合併。 例子:為了解釋並查集的原理,我將
一、並查集 (Union-Find Set)
如果:給出各個元素之間的聯絡,要求將這些元素分成幾個集合,每個集合中的元素直接或間接有聯絡。在這類問題中主要涉及的是對集合的合併和查詢,因此將這種集合稱為並查集。 連結串列被普通用來計算並查集.表中的每個元素設兩個指標:一個指向同一集合中的下一個元素;另一個指向表首元素。 鏈結構的並查集 採用鏈式儲
並查集 (Union-Find Sets)及其應用
並查集 (Union-Find Sets) 並查集:(union-find sets)是一種簡單的用途廣泛的集合. 並查集是若干個不相交集合,能夠實現較快的合併和判斷元素所在集合的操作,應用很多。一般採取樹形結構來儲存並查集,並利用一個rank陣列來儲存集合的深度下界,在查
並查集(Union-Find Algorithm),看這一篇就夠了
動態連線(Dynamic connectivity)的問題 所謂的動態連線問題是指在一組可能相互連線也可能相互沒有連線的物件中,判斷給定的兩個物件是否聯通的一類問題。這類問題可以有如下抽象: 有一組構成不相交集合的物件 union: 聯通兩個物件
並查集(union-find)模板
#include<cstdio> #include<cstring> #include<vector> using namespace std; const int mx = 100005; int fa[mx], rk[mx]; ve
並查集(Union-Find)
在電腦科學中,並查集是一種樹型的資料結構,用於處理一些不交集(Disjoint Sets)的合併及查詢問題。有一個聯合-查詢演算法(union-find algorithm)定義了兩個用於此資料結構的操
並查集(Union-Find) 應用舉例 --- 基礎篇
本文是作為上一篇文章 《並查集演算法原理和改進》 的後續,焦點主要集中在一些並查集的應用上。材料主要是取自POJ,HDOJ上的一些演算法練習題。 首先還是回顧和總結一下關於並查集的幾個關鍵點: 以樹作為節點的組織結構,結構的形態很是否採取優化策略有很大關係,未進行優化的
POJ 1182 食物鏈 [資料結構-並查集 union-find sets]
在輸入時可以先判斷題目所說的條件2和3,即: 1>若(x>n||y>n):即當前的話中x或y比n大,則假話數目num加1. 2>若(x==2&&x==y):即當前的話表示x吃x,則假話數目num加1. 而不屬於這兩種情況外的話語要利用
並查集(不相交集合)詳解與java實現
目錄 認識並查集 並查集解析 基本思想 如何檢視a,b是否在一個集合? a,b合併,究竟是a的祖先合併在b的祖先上,還是b的祖先合併在a上? 其他路徑壓縮?
並查集之 Find函式
發現自己寫了兩道題都把Find函式寫得一塌糊塗。。。一題是沒有路徑壓縮過不了,一題是因為前面寫錯過弄混了,不三不四的。。。總結很重要啊!! 路徑壓縮:遞迴寫法: int Find (int x) { if(Father[x] != x) { Fathe
