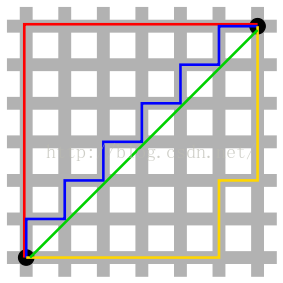
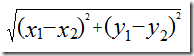曼哈頓距離,歐式距離,餘弦距離
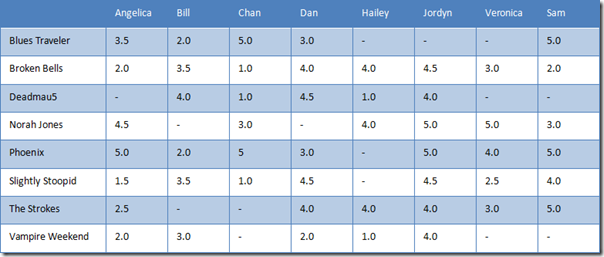
1.曼哈頓距離
曼哈頓距離又稱馬氏距離(Manhattan distance),還見到過更加形象的,叫出租車距離的。具見上圖黃線,應該就能明白。
計算距離最簡單的方法是曼哈頓距離。假設,先考慮二維情況,只有兩個樂隊 x 和 y,使用者A的評價為(x1,y1),使用者B的評價為(x2,y2),那麼,它們之間的曼哈頓距離為 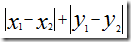
2.歐式距離
歐式距離又稱歐幾里得距離或歐幾里得度量(Euclidean Metric),以空間為基準的兩點之間最短距離,與之後的切比雪夫距離的差別是,只算在空間下。說的通俗點,就是初中知識,兩點之間直線最短的概念。
除了曼哈頓距離外,還可以計算兩個使用者之間的歐式距離。
還是先考慮兩個樂隊 x 和 y 的情況,假設,使用者A=(x1,y1),使用者B=(x2,y2),那麼它們之間的歐式距離:
3.餘弦距離
餘弦距離,也稱為餘弦相似度,是用向量空間中兩個向量夾角的餘弦值作為衡量兩個個體間差異的大小的度量。
向量,是多維空間中有方向的線段,如果兩個向量的方向一致,即夾角接近零,那麼這兩個向量就相近。而要確定兩個向量方向是否一致,這就要用到餘弦定理計算向量的夾角。
餘弦定理描述了三角形中任何一個夾角和三個邊的關係。給定三角形的三條邊,可以使用餘弦定理求出三角形各個角的角度。假定三角形的三條邊為a,b和c,對應的三個角為A,B和C,那麼角A的餘弦為:
如果將三角形的兩邊b和c看成是兩個向量,則上述公式等價於:
其中分母表示兩個向量b和c的長度,分子表示兩個向量的內積。
總之:
採用哪種距離度量方法對最終結果有很大影響。例如,你的資料集有很多特徵,但是如果任
意一對個體之間的歐氏距離都相等,那麼你就沒法通過歐氏距離進行比較了!曼哈頓距離在某些
情況下具有更高的穩定性,但是如果資料集中某些特徵值很大,用曼哈頓距離的話,這些特徵會
掩蓋其他特徵間的鄰近關係。最後,再來說說餘弦距離,它適用於特徵向量很多的情況,但是它
丟棄了向量長度所包含的在某些場景下可能會很有用的一些資訊。