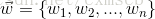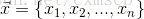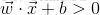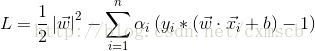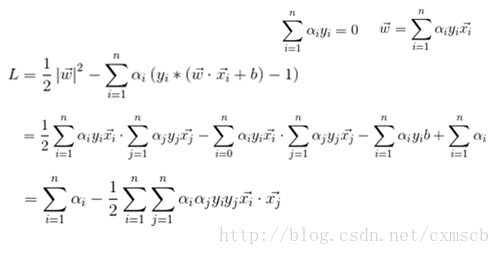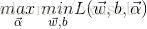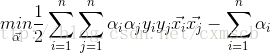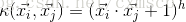一、線性可分SVM

SVM演算法最初是用來處理二分類問題的，是一種有監督學習的分類演算法。

對於線性可分的二分類問題，我們可以找到無窮多個超平面，將兩類樣本進行區分。(超平面：一維中是一個點；二維中是一條線；三維中是一個面……)

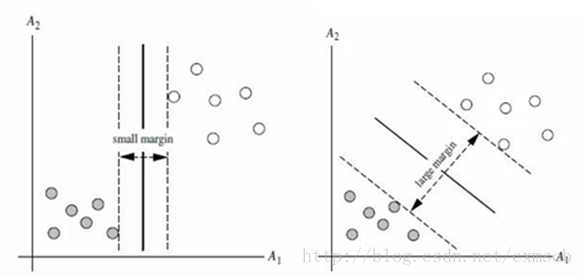
在上面的多個超平面中，它們都可以成功將樣本集劃分兩邊，但哪一個超平面更好？

一般來說，當樣本點離超平面越近，樣本的標籤為某型別的概率應該為0.5左右，確信度比較低，而樣本點離超平面越遠，樣本的標籤為某型別的概率越大，確信度比較高。

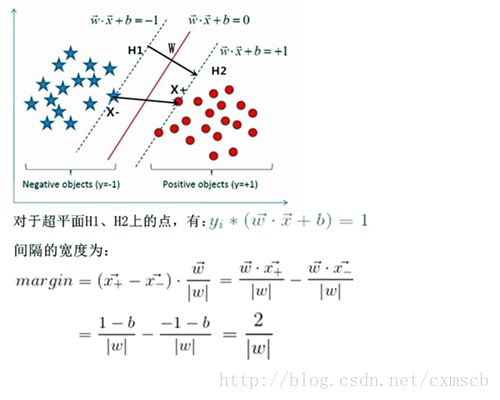
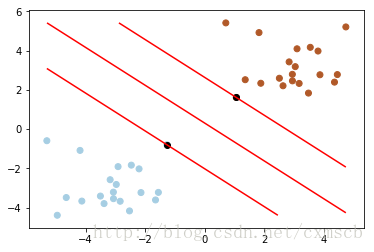
而線性可分SVM所尋找的最優超平面就是要儘可能的遠離所有類別的資料點，使得間隔（margin）最大，利用間隔最大化來求得最優超平面。間隔的定義如下圖所示：

一般來說，間隔（Margin）中間是無點區域。為了偏袒於某一類樣本，超平面到兩類樣本點集合的最小距離都是相等的，即間隔等於超平面到兩類樣本集的最小距離*2。對於間隔越大的超平面，分類犯錯的機率就越小，分類的確信度就越高。

二、超平面和間隔

接下來，需要做的就是將間隔(Margin)進行最大化，來尋找最優超平面。在這之前，需要對超平面進行定義，以便於計算點到超平面距離。

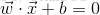
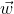
可將超平面定義為 ，向量 為超平面的法向量，標量 b 為截距。

向量 x 為樣本的特徵向量。而向量 x 點乘 向量 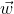可理解為向量 x 在 向量 w 上未進行歸一化的投影。

通過這樣定義超平面後，由圖可以發現：所有在超平面右上方的樣本點都有

，所有在超平面左下方的樣本點都有 。

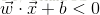當然，所有在超平面上的點都有 。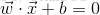

進一步，我們可以通過等比例縮放 法向量 和 截距 b，使得：

其中， 為第 i 個樣本的特徵向量，並將正樣本的標籤令作 1，負樣本的標籤令作 -1；這樣這兩個式子整合為一個式子：

。

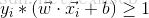
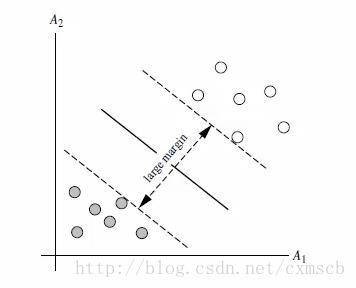
具體效果如圖所示：

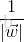
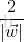
而“支援向量”就是所有落在間隔兩邊的超平面H1、H2上的點，超平面H1、H2上的任意一點（支援向量）到分界超平面的距離為 。因此，隔間的寬度應該為 。

具體的公式推導如下：

三、最大化間隔

在上面，我們找到了間隔(margin)的表示式為 ，也找到了向量w的約束條件為

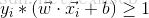。即我們需要在約束條件 下得到最大化的間隔。

為了方便計算，這裡將 最大化間隔 變換為 最小化 。

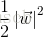
最後可變換為最優化問題，即：

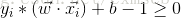
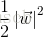
在約束條件 下取得 的最小值。

我們可以 拉格朗日乘子法 來解決這個問題。由拉格朗日乘子法，可以得到一個新的函式如下：

其中 為第i個乘子，且大於等於 0 。

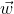
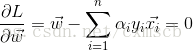
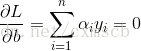
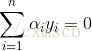
然後在這個函式上分別對 向量 和 b 求偏導，並令偏導等於0。可有以下兩個等式：

，可得到

，可得到

將上面得出的兩個式子代入L函式中，有：

可以發現，函式L與訓練集中樣本的特徵向量的兩兩點乘有關。

接下來，根據拉格郎日對偶性，將原始問題的對偶問題是極大極小問題：

接下來求 對 的極大：

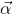
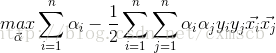
s.t. 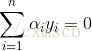， 大於等於 0 .

將極大問題轉換為轉換為對偶的極小最優化問題：

同樣 s.t. 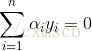， 大於等於 0 .

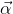
通過對 偏導 和 對 = 0 的情況進行求得最小值 / SMO 演算法，可解得到最優解 。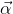

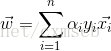
得到最優解 後，可得到法向量的最優解 ，再將 “支援向量” 代入函式中，通過移項可得到最優解 b 。

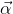
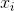
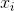
支援向量與 的關係：當向量 不是“支援向量”時， 等於0；當向量 為“支援向量”時， 不等於0。

因為在決定分離超平面時只有支援向量起作用，SVM訓練出來的模型完全依賴於支援向量，即使訓練集裡面所有 非支援向量的樣本點都被去除，結果仍然會得到完全一樣的模型。

因此超平面可以表示為：

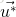
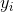
其中 為待測試的樣本的特徵向量， 為 第i個訓練樣本的標籤（1 / -1）。

當將 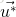測試樣本代入 d 中後，若 d < 0，則測試樣本的標籤為-1；若 d > 0，則測試樣本的標籤為1；

四、從硬間隔到軟間隔

有些時候，當存在噪聲樣本時，訓練集的樣本集並不能被嚴格地線性可分（即使使用了後面的核函式）。如圖所示：

如果硬著堅持按照原來的約束條件 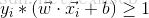考慮所有的樣本點，在此基礎上尋找正負類之間的最大間隔，就會使得整個問題無解。這種解法也叫做“硬間隔”( hard margin )分類法，因為它硬性地要求所有樣本點都滿足和分類平面間的距離必須大於某個值。

從圖中可看出，硬間隔的分類法容易受少數點的控制，為了解決這種控制，可以允許一些點到分類平面的距離不滿足原先的要求。

原先我們的硬約束條件為：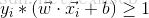

為了引入容錯性，對每個樣本點引入一個鬆弛變數 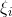，現在我們的軟約束條件為：

當某些點比較特殊時（比較離群），新的約束條件意味著我們放棄了對這些點的精確分類，而這對分類器來說是種損失。但損失這些特殊點也帶來了一些好處，那就是使超平面不必向這些點的方向移動，因而可以得到更大的間隔margin。

因為為了權衡這種損失和好處，即減小損失且又擴大間隔，我們的目標函式也需要發生改變，即我們需要最小化的函式為：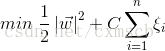

其中n為訓練集樣本的個數；把損失加入到目標函式後，需要一個懲罰因子C，C是模型的一個超引數 。這種方法也叫作 一階軟間隔分類器 。

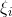
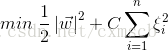
當公式中的 的階為2時，即最小化損失函式為 ，這種方法叫作 二階軟間隔分類器 。

又因為 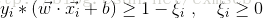， 因此損失函式可變換為：

這裡引入了 Hinge Loss 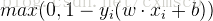： ，當樣本點距離邊界太遠時，該樣本點的 Hinge Loss 為 0 。

當懲罰因子C越大時，被誤分類的樣本點的個數就越小。上面的公式中，所有樣本點共用了一個懲罰因子，當然，也可以是不同的樣本點可以對應不同的懲罰因子。

五、從線性到非線性

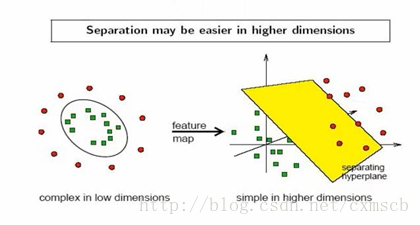
上面只是說明了線性可分的情況，而針對線性不可分的情況：

訓練集的樣本在當前維度的空間對應的向量找不到一個超平面來區分開。對於這種情況，一種處理方法是 對特徵向量進行非線性對映，對映到一個更高維的空間，然後再在高維空間中尋找最優超平面，但計算內積時演算法複雜度非常高；另一種處理方法為 核方法（kernel trick），用一個核函式來 取代 經對映之後的向量的內積，解決複雜度的問題。

具體例子可如下圖所示：

若用f表示這個非線性的對映，那麼核函式等同於經f對映之後的兩個向量的內積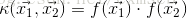： ，等式左邊的計算複雜度往往低於右邊的計算複雜度。

複雜度的比較例子如下圖所示：

常見的核函式有：

h度多項式核函式：

高斯核函式RBF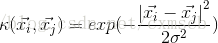： ， 其中 gamma 為超引數。

一般根據先驗知識來選擇相應的核函式，可嘗試不同的核函式，根據實驗結果來確定。

六、從二分類到多分類

在上面，我們討論的都是使用SVM來二分類問題。對於多分類問題，可以通過擴充套件SVM，通過one-vs-rest的方法來解決多分類問題，這樣的解決方法一般會有很多個SVM：有多少類標籤，就會有多少個SVM。

七、SVM與LR的區別

1. 對於線性模型，決定SVM得到的直線位置並不是所有的訓練樣本，而是那些支援向量；而邏輯迴歸模型在訓練模型中考慮了所有訓練樣本對引數的影響。這個可以本質上從損失函式上看出來。

2. 在解決非線性問題時，支援向量機採用核函式的機制，而LR通常多項式化特徵的方法。

3. 邏輯迴歸的損失函式是logistic loss，而SVM的損失函式是hinge loss ：

八、程式碼示例

import numpy as np
import matplotlib.pyplot
from sklearn import svm

np.random.seed(8) # 保證隨機的唯一性

# 線性可分：
array = np.random.randn(20,2)
X = np.r_[array-[3,3],array+[3,3]]
y = [0]*20+[1]*20
print X[0]
print X[20]
print y

[-2.90879528 -1.90871727]
[ 3.09120472  4.09128273]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]

# 建立svm模型
clf = svm.SVC(kernel='linear')
clf.fit(X,y)

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape=None, degree=3, gamma='auto', kernel='linear',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False)

x1_min, x1_max = X[:,0].min(), X[:,0].max(),
x2_min, x2_max = X[:,1].min(), X[:,1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
# 得到向量w  : w_0x_1+w_1x_2+b=0
w = clf.coef_[0]
f = w[0]*xx1 + w[1]*xx2 + clf.intercept_[0]+1  # 加1後才可繪製 -1 的等高線 [-1,0,1] + 1 = [0,1,2]
plt.contour(xx1, xx2, f, [0,1,2], colors = 'r') # 繪製分隔超平面、H1、H2
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.Paired) 
plt.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],color='k') # 繪製支援向量點
plt.show()

# 非線性可分：

from sklearn import datasets

# 載入資料
iris = datasets.load_iris()
X = iris.data
y = iris.target
print iris.target_names

['setosa' 'versicolor' 'virginica']

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=1/3.) # 分割訓練集和測試集

from sklearn.preprocessing import StandardScaler # 標準化

scaler = StandardScaler()
X_train_std = scaler.fit_transform(X_train)
X_test_std = scaler.transform(X_test)

from sklearn.grid_search import GridSearchCV

# 交叉驗證，調整引數

param_grid = {'C':[1e1,1e2,1e3, 5e3,1e4,5e4],
              'gamma':[0.0001,0.0008,0.0005,0.008,0.005,]}
clf = GridSearchCV(svm.SVC(kernel='rbf',class_weight='balanced'),param_grid,cv=10)
clf = clf.fit(X_train_std,y_train)
print clf.best_estimator_

SVC(C=10.0, cache_size=200, class_weight='balanced', coef0=0.0,
  decision_function_shape=None, degree=3, gamma=0.005, kernel='rbf',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False)

clf.score(X_test_std,y_test)

1.0

y_pred = clf.predict(X_test_std)

from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix

print(classification_report(y_test,y_pred,target_names=iris.target_names))
print(confusion_matrix(y_test,y_pred,labels=range(iris.target_names.shape[0])))

             precision    recall  f1-score   support

     setosa       1.00      1.00      1.00        18
 versicolor       1.00      1.00      1.00        17
  virginica       1.00      1.00      1.00        15

avg / total       1.00      1.00      1.00        50

# recall表示召回率 = #(True positive) / (#(True positive)+ #(False negative))，表示樣本中的正例有多少被預測正確。

# precision表示精確率 = #(True positive) / (#(True positive)+ #(False negative))，表示預測為正的樣本中有多少是真正的正樣本。

# f1-score（F1指標）表示召回率和精確率兩個指標的調和平均數，召回率和精確率越接近,F1指標越高。F1 = 2 / （1/recall + 1/precision）。召回率和精確率差距過大的學習模型，往往沒有足夠的實用價值。



[[18  0  0]
 [ 0 17  0]
 [ 0  0 15]]

縱座標表示預測的是誰，橫座標表示標準的是誰。對角線的值越大，預測能力越好。