1.SVM的原理與目標

1.1 分割超平面

來看上圖，假設C和D是兩個不想交的凸集，則存在一個超平面P，這個P可以將C和D分離。

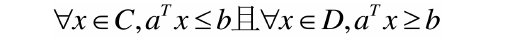
這兩個集合的距離，定義為兩個集合間元素的最短距離。

做集合C和集合D最短線段的垂直平分線。這條垂直平分線就是分割超平面。

在兩個集合之間，可以有無數條分割超平面，使其將兩個集合分離，但是如何定義與找出兩個集合的“最優”分割超平面呢？

可以這樣做： 
找到集合“邊界”上的若干點，以這些點為基礎計算超平面的方向，以兩個集合 邊界上的這些點的平均作為超平面的“截距” 
因為超平面是通過這些點（向量）來支撐形成的，所以我們叫這些吃撐了超平面產生的向量叫做支援向量,support vector.

那麼如果兩個集合有部分相交，如何定義超平面，從而使得兩個集合儘量分開呢？

如下圖，在兩個集合之間可以畫出無數條超平面，到底哪條是最好的，到底哪些是支援向量呢？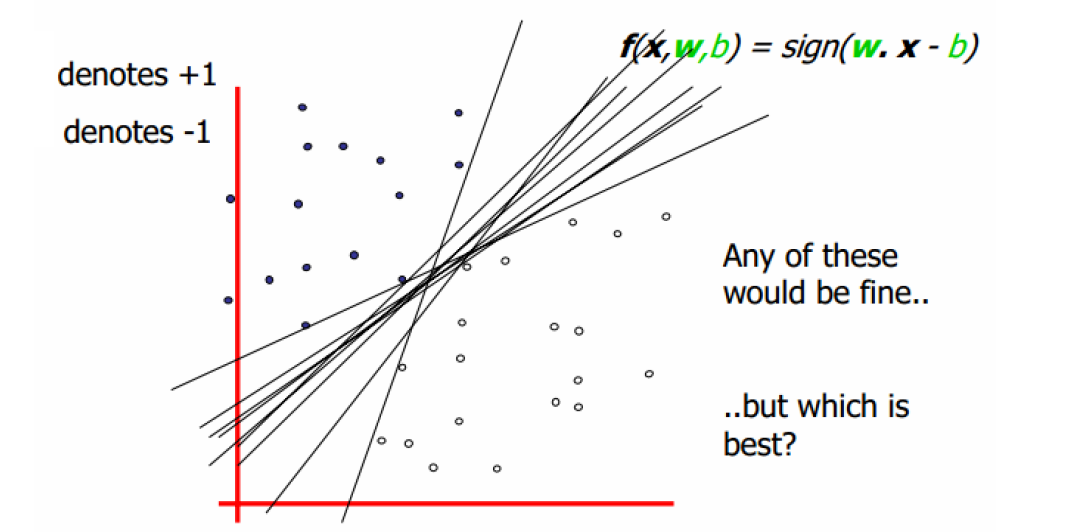 

1.2 定義輸入資料

假設給定一個特徵空間上的訓練集為：

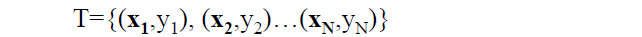
其中，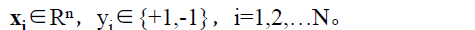

xi為第i個例項（樣本），若n>1,則xi為向量。

yi為xi的標記： 
當yi=1時，xi為正例 
當yi=-1時，xi為負例 
（至於為什麼正負用（-1，1）表示呢？這個問題也許從來沒有想過。其實這裡沒有太多原理，就是一個標記，你也可以用正2，負-3來標記。只是為了方便，yi/yj=yi*yj的過程中剛好可以相等，便於之後的計算。）

（xi,yi)稱為樣本點。

1.3 線性可分支援向量機

給定了上面提出的線性可分訓練資料集，通過間隔最大化得到分離超平面為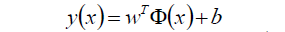 

相應的分類決策函式為：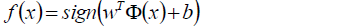 

以上決策函式就稱為線性可分支援向量機。

這裡解釋一下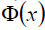這個東東。 
這是某個確定的特徵空間轉換函式，它的作用是將x對映到更高的維度。 
比如我們看到的特徵有2個：x1,x2,組成最見到的線性函式可以是w1x1,w2x2.但也許這兩個特徵並不能很好地描述資料，於是我們進行維度的轉化，變成了w1x1+w2x2+w3x1x2+w4x1^2+w5x2^2.於是我們多了三個特徵。而這個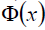就是籠統地描述x的對映的。 
最簡單直接的就是：

以上就是線性可分支援向量機的模型表示式。我們要去求出這樣一個模型，或者說這樣一個超平面y(x),它能夠最優地分離兩個集合。 
其實也就是我們要去一組引數（w,b),使其構建的超平面函式能夠最優地分離兩個集合。

如下就是一個最優超平面： 

又比如說這樣：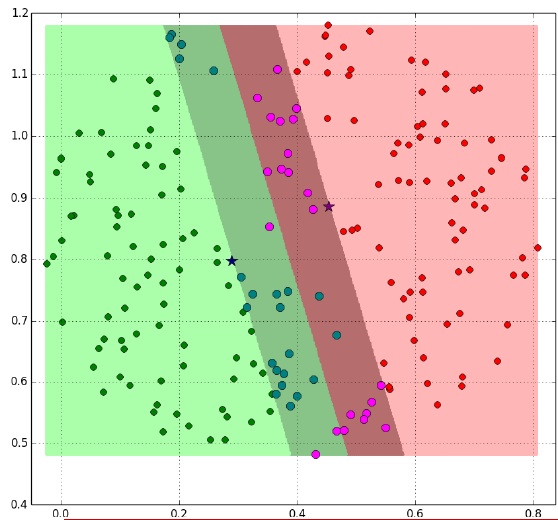 

陰影部分是一個“過渡帶”，“過渡帶”的邊界是集合中離超平面最近的樣本點落在的地方。

2.SVM的計算過程與演算法步驟

2.1 推導目標函式

我們知道了支援向量機是個什麼東東了。現在我們要去尋找這個支援向量機，也就是尋找一個最優的超平面。

於是我們要建立一個目標函式。那麼如何建立呢？

再來看一下我們的超平面表示式： 

有：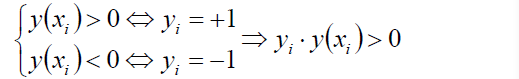 

如果這個點落在超平面的上方，那麼y就大於0，為正例，反之則為負例。無論正例還是負例，yi * y(xi)總是會大於0.

如果w,b等比縮放，則t*y的值同樣縮放，所以有：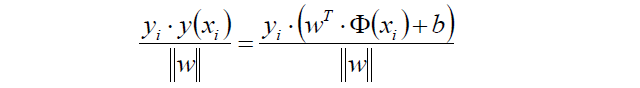 

通過上式可以得到目標函式：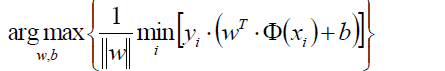 

首先是把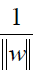這個東東提出來在外面。

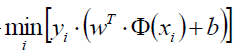表示對某一個（w,b）的引數組合（也就是對某一個超平面）遍歷所有的樣本點xi，求該樣本點到超平面的距離，然後取一個最小的距離。

最外層的max(w,b)表示在所有的（w,b)的組合中（也就是在所有的超平面中），選出那個擁有最大的最短距離的超平面。這個超平面就是我們要尋找的最優超平面。

2.2 轉換目標函式

我們有了目標函數了，但建立目標函式的故事還沒有完。為了計算的方便，目標函式還要進一步地化簡化簡，直到處女座們會心一笑為止。

再來看一下我們的分割平面： 
|y|總是>=0的。

然而我們總可以通過等比例地縮放w的方法，使得兩類點的函式值都滿足|y| >= 1。 
如果|y| >= 1這個條件滿足，那麼我們的原目標函式：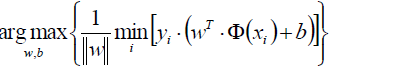 

就可以瘦身成新的目標函式： 

這個新的目標函式有個約束條件，就是： 

來來來，教科書裡標準的寫法：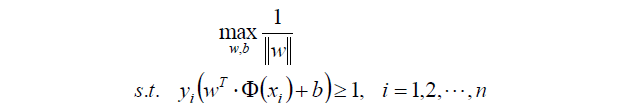 

上面求最大值可以轉換成求最小值的函式：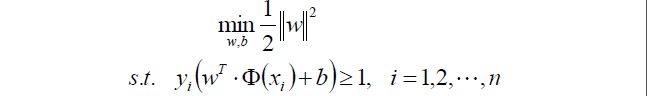 

||w||其實就是開根號的（w1^2+w2^2…wn^2), 
所以||w||^2就剛好把裡面的根號去掉了。

乘以一個1/2是我了等等求導的方便。

2.3 目標函式的求解

終於把目標函式給建立起來了。那麼下一步自然是去求目標函式的最優值嘍~

因為目標函式帶有一個約束條件，所以我們可以用拉格朗日乘子法求解。

啥是拉格朗日乘子法呢？這邊小小回顧一下。 
如果函式f(x)= 2x+1,約束條件是x+1>0, 
那麼目標函式可以轉換為： 
f(x) = 2x+1 - α(x+1)

於是我們的目標函式就轉換為了：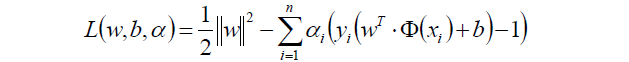 

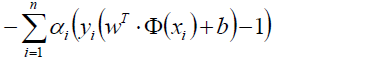中將約束條件-1，所以這一部分的值肯定滿足>=0了。

走到這一步，這個目標函式還是不能開始求解，現在我們的問題是極小極大值問題： 

我們要將其轉換為對偶問題，變成極大極小值問題：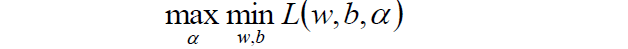 

如何獲取對偶函式？ 
首先我們對原目標函式的w和b分別求導： 
原目標函式：

對w求導：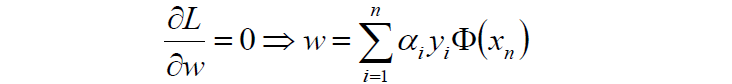 

對b求導：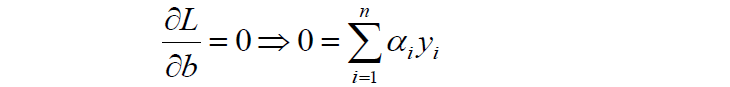 

然後將以上w和b的求導函式重新代入原目標函式的w和b中，得到的就是原函式的對偶函式： 

這個對偶函式其實求的是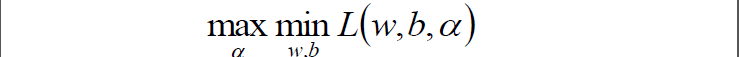中的minL(w,b)部分（因為對w,b求了偏導）。

於是現在要求的是這個函式的極大值max(a),寫成公式就是：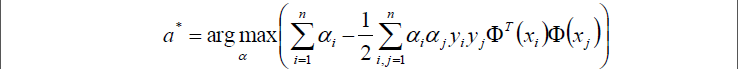 

好了，現在我們只需要對上式求出極大值a*，然後將a*代入w求偏導的那個公式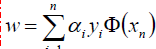 
從而求出w.

將w代入超平面的表示式，並且將所有樣本點都代入，再除以2，就可以得到b了。

現在的w,b就是我們要尋找的最優超平面的引數。

我們用數學表示式來說明上面的過程： 
1.首先是求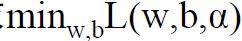的極大值。即：

 
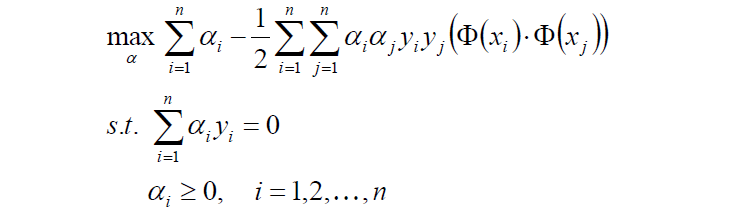
注意有兩個約束條件。

2.對目標函式新增符號，轉換成求極小值：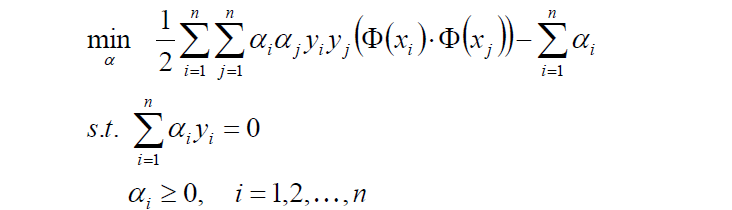 

3.計算上面式子的極值求出a*

4.將a*代入，計算w,b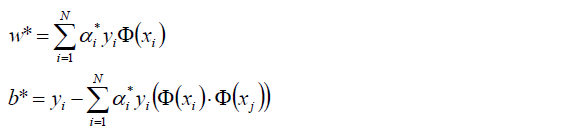 

5.求得超平面：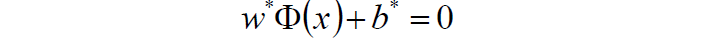 

6.求得分類決策函式：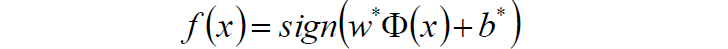 

2.4 例子

給定3個數據點：正例點x1=(3,3),x2=(4,3),負x3=(1,1),求線性可分支援向量機。 
三個點畫出來：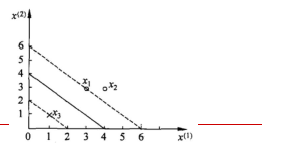 

1.首先確定目標函式

2.求得目標函式的極值

3.將求得的極值代入從而求得最優引數w,b 
a1=a3=1/4對應的點x1,x3就是支援向量機 
代入公式：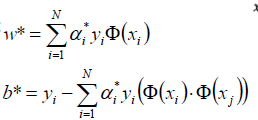 

得到w1=w2=0.5, b=-2

4.因此得到分離超平面為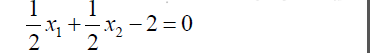 

5.得到分離決策函式為：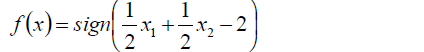 

3.線性支援向量機–軟間隔最大化

上文第一節與第二節將的都是線性可分支援向量機，也就是說肯定可以找出一個超平面來完全得分割兩個集合。

那麼是不是分類完全正確的超平面就是最好的呢？

像下圖這樣的例子，黑色實線完全地將兩個集合分開了，但是很明顯，我們仍然感覺虛線更好，雖然如果將虛線作為分割面有一個樣本被分錯了，但是它具有更好的泛化能力。如果畫出過渡帶的話，實現的過渡帶會非常窄，而虛線的過渡帶則比較寬。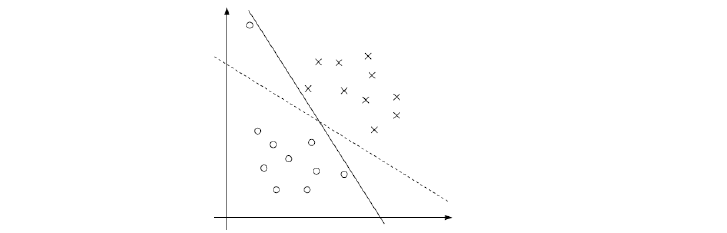 

完美地分割面並不是最優的，而且往往還會導致過擬合。我們的樣本資料中可能存在的異常值或噪聲往往也會導致完美的分割並不完美。對它們的忽視也許會有利於找到更好的分離超平面。

另外，在實際應用中，樣本資料往往是線性不可分的，我們根本找不到一個超平面去完全隔離兩組資料。

3.1 目標函式及其計算

若資料線性不可分，則增加鬆弛因子ξi>=0. 
使函式間隔加上鬆弛變數大於等於1. 
如此的話約束條件就變成了： 

目標函式就變成了： 
 
這個係數C細究一下，如果C為正無窮，那麼ξ必須等於0才能使整個公式求得最小值。如果ξ為0的話，就是沒有鬆弛因子，求出來的就是線性可分支援向量機的最優超平面。隨著ξ越來越小，超平面會慢慢地趨於泛化，下面這個圖中的實現會慢慢變成虛線。 

同樣對目標函式進行拉格朗日函式的轉換：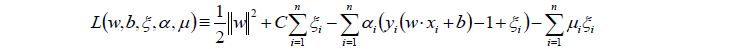 

然後對w,b,ξ分別求偏導： 

將以上三個求偏導的式子代入L中，得到：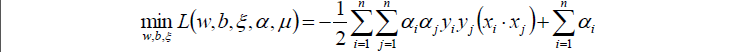 

對上式再求極大值：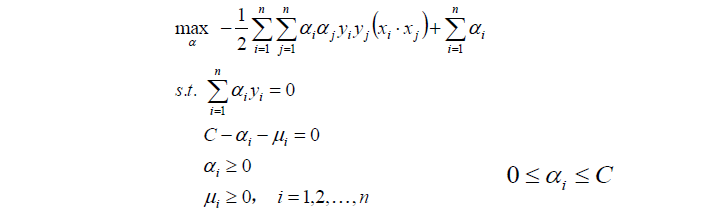 
 
其實，我們發現，目標函式與線性可分支援向量機是一樣的，不一樣的是約束條件。

上面的約束條件可以經過變化，最終得到對偶問題：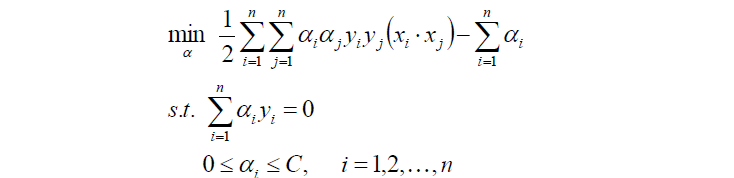 

然後對以上式子求最優值a*

將a*代入並計算w,b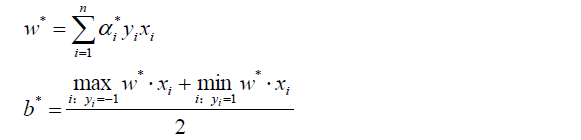 
 
注意，計算b*時，需要使用滿足條件0 < aj

3.2 損失函式

如下圖，分別有三類損失函式

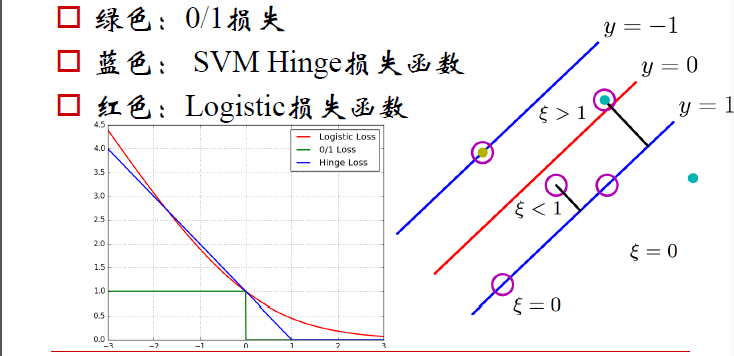
綠色：0/1損失 
當負例的點落在y=0這個超平面的下邊，說明是分類正確，無論距離超平面所遠多近，誤差都是0. 
當這個負例的樣本點落在y=0的上方的時候，說明分類錯誤，無論距離多遠多近，誤差都為1.

藍色：SVM Hinge損失函式 
當一個負例的點落在y=1的直線上，距離超平面長度1，，那麼1-ξ=1，ξ=0； 
當它落在距離超平面0.5的地方，1-ξ=0.5，ξ0.5，也就是說誤差為0.5； 
當它落在Y=0上的時候，距離為0，1-ξ=0，ξ=1，誤差為1； 
當這個點落在了y=0的上方，被誤分到了正例中，距離算出來應該是負的，比如-0.5，那麼1-ξ=-0.5，ξ=-1.5.誤差為1.5. 
以此類推，畫在二維座標上就是上圖中藍色那根線了。

紅色：LOGISTIC損失函式 
損失函式的公式為：ln(1+e^-yi) 
當yi=0時，損失等於ln2,這樣真醜，所以我們給這個損失函式除以ln2. 
這樣到yi=0時，損失為1，即損失函式過（0，1）點 
及時圖中的紅色線。

4.核函式

SVM+核函式具有極大威力。核函式並不是SVM特有的，核函式可以和其他演算法也進行結合，只是核函式與SVM結合的優勢非常大。

4.1 什麼是核函式

核函式，是將原始輸入空間對映到新的特徵空間，從而，使得原本線性不可分的樣本可能在核空間可分。

之前我們講的Φ(xi)是第i個樣本的特徵，Φ(xj)是第j個樣本的特徵。現在我們將兩個樣本做一個點乘，並且用k(xi,xj)表示： 
k(xi,xj) = Φ(xi) * Φ(xj)

這個k(xi,xj)我們就定義核函式。它是類似於相似度的一個東東。

i可以取值為1->n，j也可以取值為1->n,通過核函式的轉換就變成了n*n的一個矩陣:

j/i	1	2	…	n
1	k11	k12	…	k1n
2	…	…	…	k2n
…	…	…	…	…
n	kn1	kn2	…	…

注意xi和xj是兩個樣本，如果是特徵的維度只有1，那麼x就是一個值，如果維度大於等於2，那麼x就是一個特徵向量。但是k(xi,xj)永遠都是一個值。

核函式有很多很多種類，比如：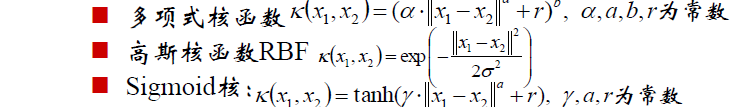 

在實際中選擇何種核函式呢？ 
選擇核函式，往往依賴先驗領域知識，或者通過交叉驗證等方法來選擇有效的核函式。

如果沒有更多的先驗資訊，則選擇使用高斯核函式。

4.2 核函式的對映

我們以高斯核函式為例。 
假設任意兩個點x1,x2. 
||x1-x2||表示x1-x2的模也就是x1與x2的直線距離d。 
||x1-x2||^2就是兩點距離d的平方。 
將d^2再除以2sigma平方，然後前面加個負號 
於是從高斯核函式的公式中可以看出，如果距離d越大，則兩個點的相似性越小，而k(x1,x2)也越小，反之亦然。所以我們說核函式就是類似於相似性的一個描述。

既然是相似性，那距離為0的核函式k就=1，距離越遠的話，k就越小。 
對樣本點x1,我們可以把所有樣本點都和x1求一個k值，那麼必然是以x1為中心點，向外一層層畫圓，每個圓環上的點都與x1的k值相同，越外的圓k值就越小。就好像一組等高線。正例的在上方形成一個山峰，負例的在下方形成一個山谷。那麼對每個樣本點都這樣做一次。於是畫在三維圖上就是如下樣子：

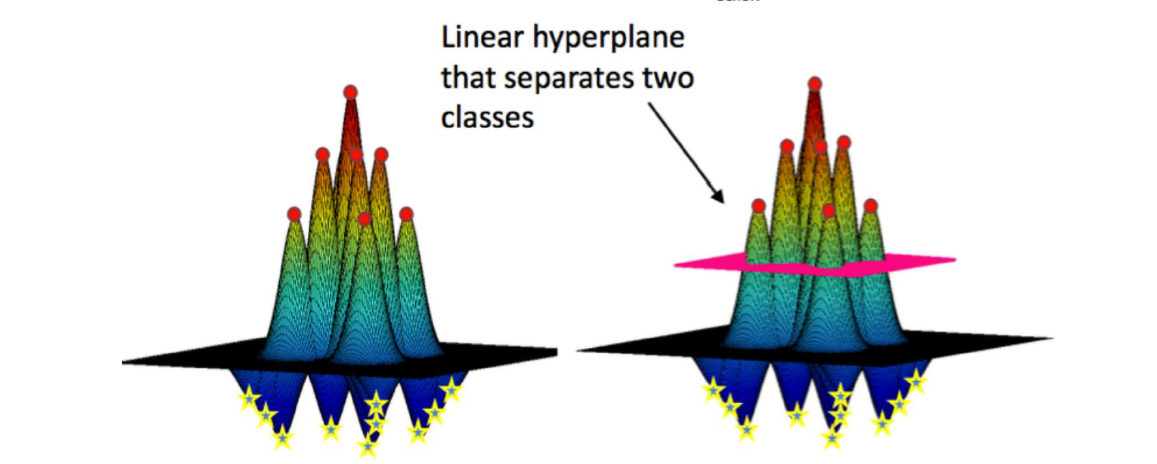
所有的山峰會組成一個大山峰，所有的山谷也會組成一個大山谷，所以，就形成了右下圖的樣子。 

可以看到上圖中有一個平面可以將這一整個山切開，上面是正例點，下面是負例點。加這個平面轉換到二維左邊的樣本點圖中就是一條分割紅藍點的曲線（分割超平面）。

也就是說，我們將低維的樣本點對映到高維，在高維中找到一個最優的分割超平面，然後再將超平面轉換到低維中的一條曲線。

那麼如何在高維中尋找一個最優分割超平面呢？這個就又回到了我們上面講的SVM支援向量機的尋找分割超平面的問題了。 
所以說核函式與SVM真的是搭配得天衣無縫。

4.3 高斯核

高斯核是什麼樣的，上面已經講了。高斯核還有一個特性–就是“高斯核是無窮維的”。

下面這個公式是可以證明得到的，這裡不講如何證明：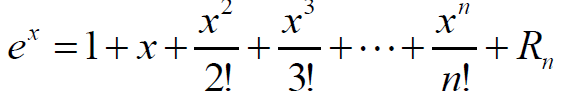 

將上面這個公式代入高斯核函式中：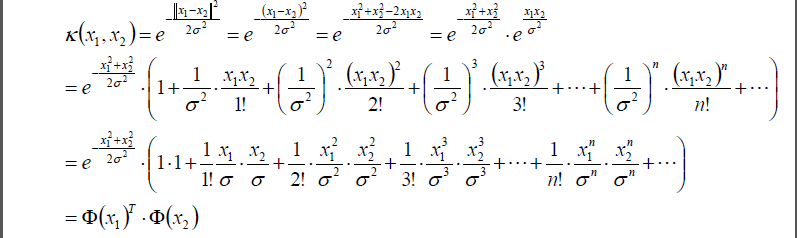 

其中，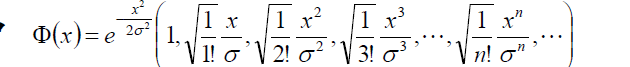 

無窮維的高斯核，也就說可以將低維空間的樣本構造成如何維度，可以構造任何一種存在的可能。所以，對於一組訓練樣本，高斯核函式總能有一種方式可以實現對訓練樣本的100%的擬合。（雖然100%的擬合併不是我們想要的，因為那樣會導致過擬合）

5.SMO演算法

SMO：Sequential Minimal Optimization序列最小最優化

回顧之前的目標函式求解，函式中有多個拉格朗日乘子a11，a2,..an。 
現在對其中兩個乘子做優化，其他因子認為是常數。這樣就將N個解的問題轉換成了兩個變數的求解問題，並且目標函式是凸的。求解完之後，將這兩個因子剔除掉，然後繼續選另外兩個來做優化，以此類推。

下面是求解過程（直接擷取鄒博老師的PPT） 

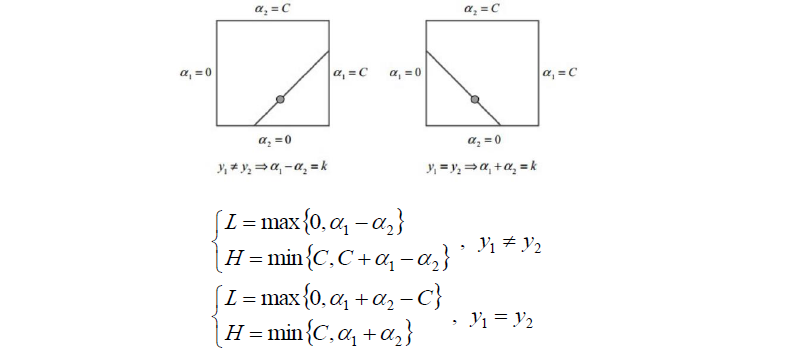
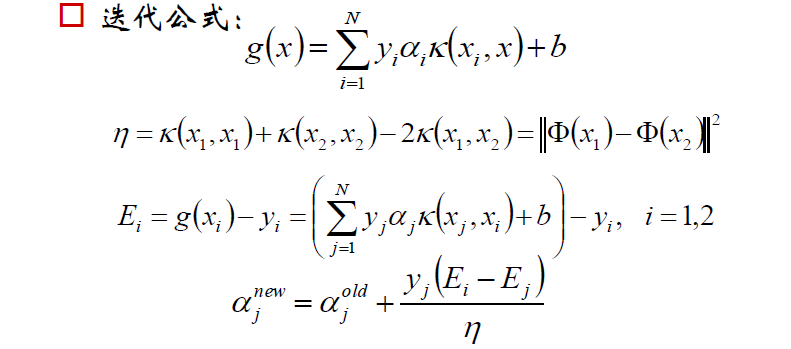
Soft Margin和SVM中的正則化

"""scikit-learn中的SVM"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris=datasets.load_iris()
X=iris.data
y=iris.target

X=X[y<2,:2]
y=y[y<2]

plt.scatter(X[y==0,0],X[y==0,1],color='red')
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()

"""使用SVM之前一定要先進行資料歸一化"""
standardScaler=StandardScaler()
standardScaler.fit(X)
x_standard=standardScaler.transform(X)

svc=LinearSVC(C=1e9)
svc.fit(x_standard,y)

"""繪製函式"""
def plot_decision_boundary(model,axis):
    x0,x1 = np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100))
    )
    X_new = np.c_[x0.ravel(),x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)
plot_decision_boundary(svc,axis=[-3,3,-3,3])
plt.scatter(x_standard[y==0,0],x_standard[y==0,1])
plt.scatter(x_standard[y==1,0],x_standard[y==1,1])
plt.show()

"""繪製上下兩個支撐向量的影象"""
def plot_svc_decision_boundary(model,axis):
    x0,x1 = np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100))
    )
    X_new = np.c_[x0.ravel(),x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)

    w=model.coef_[0]
    b=model.intercept_[0]

    #w0*x0+w1*x1+b=0
    #->x1=-w0/w1*x0-b/w1
    plot_x=np.linspace(axis[0],axis[1],200)
    up_y=-w[0]/w[1]*plot_x-b/w[1]+1/w[1]
    down_y=-w[0]/w[1]*plot_x-b/w[1]-1/w[1]

    up_index=(up_y>=axis[2])&(up_y<=axis[3])
    down_index=(down_y>=axis[2])&(down_y<=axis[3])
    plt.plot(plot_x[up_index],up_y[up_index],color='black')
    plt.plot(plot_x[down_index],down_y[down_index],color='black')

plot_svc_decision_boundary(svc,axis=[-3,3,-3,3])
plt.scatter(x_standard[y==0,0],x_standard[y==0,1])
plt.scatter(x_standard[y==1,0],x_standard[y==1,1])
plt.show()

結果：

 SVM中的核函式

"""SVM中使用多項式特徵"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

X,y=datasets.make_moons(noise=0.15,random_state=666)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

"""使用多項式特徵的SVM"""
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline

def PolynomialSVC(degree,C=1.0):
    return Pipeline([
        ('Poly',PolynomialFeatures(degree=degree)),
        ('std_scaler',StandardScaler()),
        ('linearSVC',LinearSVC())
    ])
poly_svc=PolynomialSVC(degree=3)
poly_svc.fit(X,y)

def plot_decision_boundary(model,axis):
    x0,x1 = np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100))
    )
    X_new = np.c_[x0.ravel(),x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)
plot_decision_boundary(poly_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

"""使用多項式核函式的SVM"""
from sklearn.svm import SVC

def PolynomialKernelSVC(degree,C=1.0):
    return Pipeline([
        ('std,scaler',StandardScaler()),
        ('KernelSVC',SVC(kernel='poly',degree=degree,C=C))
    ])
poly_kernel_svc=PolynomialKernelSVC(degree=3)
poly_kernel_svc.fit(X,y)
plot_decision_boundary(poly_kernel_svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

結果:

 

 

核函式本質

​核函式的本質可以概括為如下三點：

1）實際應用中，常常遇到線性不可分的情況​。針對這種情況，常用做法是把樣例特徵對映到高維空間中，轉化為線性可分問題。

2）將樣例特徵對映到高維空間，可能會遇到維度過高的問題​。

3）針對可能的維災難，可以利用核函式。核函式也是將特徵從低維到高維的轉換，但避免了直接進行高維空間中的複雜計算，​可以在低維上進行計算，卻能在實質上將分類效果表現在高維上。

當然，SVM也能處理線性可分問題，這時使用的就是線性核了。​

常用的核函式包括如下幾個：​線性核函式，多項式核函式，RBF核函式(高斯核)，Sigmoid核函式

 

"""高斯核函式"""
import numpy as np
import matplotlib.pyplot as plt

X=np.arange(-4,5,1)
y=np.array((X>=-2)&(X<=2),dtype='int')

plt.scatter(X[y==0],[0]*len(X[y==0]))
plt.scatter(X[y==1],[0]*len(X[y==1]))
plt.show()

def gaussian(x,l):
    gamma=1.0
    return np.exp(-gamma*(x-l)**2)

l1,l2=-1,1
X_new=np.empty((len(X),2))

for i,data in enumerate(X):
    X_new[i,0]=gaussian(data,l1)
    X_new[i,1]=gaussian(data,l2)

plt.scatter(X_new[y==0,0],X_new[y==0,1])
plt.scatter(X_new[y==1,0],X_new[y==1,1])
plt.show()

 結果：

"""scikit-learn中使用RBF核"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
X,y=datasets.make_moons(noise=0.15,random_state=666)
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('svc',SVC(kernel='rbf',gamma=gamma))
    ])

svc=RBFKernelSVC(gamma=1.0)
svc.fit(X,y)

def plot_decision_boundary(model,axis):
    x0,x1 = np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100))
    )
    X_new = np.c_[x0.ravel(),x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_cmap)
plot_decision_boundary(svc,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

 

 改變gamma的值可以改變決策邊界。

 SVM解決迴歸問題

"""SVM思想解決迴歸問題"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split

boston=datasets.load_boston()
X=boston.data
y=boston.target

X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=666)

from sklearn.svm import LinearSVR
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

def StandardLinearSVR(epsilon=0.1):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        ('linearSVR',LinearSVR(epsilon=epsilon))
    ])
svr=StandardLinearSVR()
svr.fit(X_train,y_train)
print(svr.score(X_test,y_test))