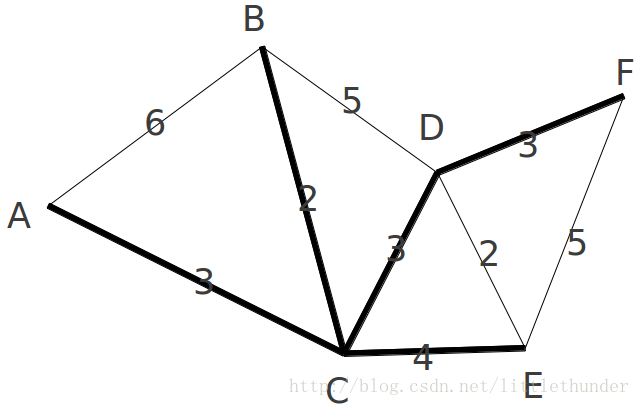
Dijkstra演算法和前一篇的Prim演算法非常像，區別就在於Dijkstra演算法向最短路徑樹（SPT）中新增頂點的時候，是按照ta與源點的距離順序進行的。OSPF動態路由協議就是用的Dijkstra演算法。下面還以那個圖的例子為例：

程式碼如下：

_=float('inf')

def dijkstra(graph,n):
	dis=[0]*n
	flag=[False]*n
	pre=[0]*n
	flag[0]=True
	k=0
	for i in range(n):
		dis[i]=graph[k][i]

	for j in range(n-1):
		mini=_
		for i in range(n):
			if dis[i]<mini and not flag[i]:
				mini=dis[i]
				k=i
		if k==0:#不連通
			return
		flag[k]=True
		for i in range(n):
			if dis[i]>dis[k]+graph[k][i]:
				dis[i]=dis[k]+graph[k][i]
				pre[i]=k
#		print(k)
	return dis,pre

if __name__=='__main__':
	n=6
	graph=[
			[0,6,3,_,_,_],
			[6,0,2,5,_,_],
			[3,2,0,3,4,_],
			[_,5,3,0,2,3],
			[_,_,4,2,0,5],
			[_,_,_,3,5,0],
			]
	dis,pre=dijkstra(graph,n)
	print(dis)
	print(pre)
 

[0, 5, 3, 6, 7, 9]
[0, 2, 0, 2, 2, 3]