【演算法導論】單源最短路徑之Dijkstra演算法
Dijkstra演算法解決了有向圖上帶正權值的單源最短路徑問題,其執行時間要比Bellman-Ford演算法低,但適用範圍比Bellman-Ford演算法窄。
迪傑斯特拉提出的按路徑長度遞增次序來產生源點到各頂點的最短路徑的演算法思想是:對有n個頂點的有向連通網路G=(V, E),首先從V中取出源點u0放入最短路徑頂點集合U中,這時的最短路徑網路S=({u0}, {}); 然後從uU和vV-U中找一條代價最小的邊(u*, v*)加入到S中去,此時S=({u0, v*}, {(u0, v*)})。每往U中增加一個頂點,則要對V-U中的各頂點的權值進行一次修正。若加進v*作為中間頂點,使得從u0到其他屬於V-U的頂點vi的路徑不加v*時最短,則修改u0到vi的權值,即以(u0, v*)的權值加上(v*, vi )的權值來代替原(u0, vi )的權值,否則不修改u0到vi的權值。接著再從權值修正後的V-U中選擇最短的邊加入S中,如此反覆,直到U=V為止。
上面的說明都很抽象,下面圖解演算法思想:
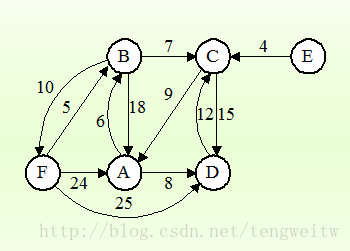
原始圖為:
尋找最短路徑的過程如下:
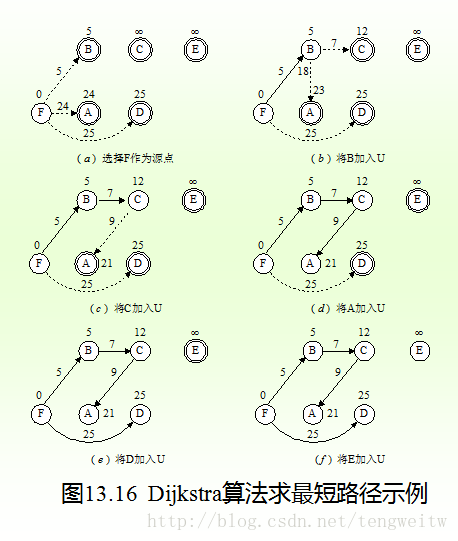
對第一個圖中的有向網路按以上演算法思想處理,所求得的從源點F到其餘頂點的最短路徑的過程如圖13.16所示。其中單圓圈表示U中的頂點,而雙圓圈表示V-U中的頂點。連線U中兩個頂點的有向邊用實線表示,連線U和V-U中兩個頂點的有向邊用虛線表示。圓圈旁的數字為源點到該頂點當前的距離值。
初始時,S中只有一個源點F,它到V-U中各頂點的路徑如圖13.16(a)所示;選擇圖13.16(a)中最小代價邊(F, B),同時由於路徑(F, A)大於(F, B, A)和(F, C)大於(F, B, C),進行相應調整可得到圖13.16(b);選擇圖13.16(b)中的最小代價邊(B, C),同時由於(F, B, A)大於(F, B, C, A),進行相應調整可得到圖13.16(c);選擇圖13.16(c)中最小代價邊(C, A)即可得到圖13.16(d);選擇圖13.16(d)中最小代價邊(F,
D) 即可得到圖13.16(e); 最後選擇(F, E)即可得到圖13.16( f )。
具體的程式實現如下:
#include<stdio.h> #define M 12//邊數 #define N 6//頂點數 #define MAX 10000 void Dijkstra(int v, int dist[][N],int D[N],int p[N],int s[N]) ; int flag[N]={0}; int flag1=0; int flag2=0; typedef struct { int startvex; int endvex; int length; }edge;//邊的結構體 edge T[M]; void main() { int dist[N][N]={{0,6,MAX,8,MAX,MAX},//圖的鄰接矩陣 {18,0,7,MAX,MAX,10}, {9,MAX,0,15,MAX,MAX}, {MAX,MAX,12,0,MAX,MAX}, {MAX,MAX,4,MAX,0,MAX}, {24,5,MAX,25,MAX,0}}; int D[N]={0}; int p[N]={0}; int s[N]={0}; int num=0; Dijkstra(5,dist,D, p,s) ; } void Dijkstra(int v, int dist[][N],int D[N],int p[N],int s[N]) { int i, j, k, v1, min, max=10000, pre; /* Max中的值用以表示dist矩陣中的值 */ v1=v; for( i=0; i<N; i++) /* 各陣列進行初始化 */ { D[i]=dist[v1][i]; if( D[i] != MAX ) p[i]= v1+1; else p[i]=0; s[i]=0; } s[v1]=1; /* 將源點送U */ for( i=0; i<N-1; i++) /* 求源點到其餘頂點的最短距離 */ { min=10001; /* min>max, 以保證值為的頂點也能加入U */ for( j=0; j<N-1; j++) if ( ( !s[j] )&&(D[j]<min) ) /* 找出到源點具有最短距離的邊 */ {min=D[j]; k=j; } s[k]=1; /* 將找到的頂點k送入U */ for(j=0; j<N; j++) if ( (!s[j])&&(D[j]>D[k]+dist[k][j]) ) /* 調整V-U中各頂點的距離值 */ {D[j]=D[k]+dist[k][j]; p[j]=k+1; /* k是j的前趨 */ } } /* 所有頂點已擴充到U中 */ for( i=0; i<N; i++) { printf(" %d : %d ", D[i], i); pre=p[i]; while ((pre!=0)&&(pre!=v+1)) { printf ("<- %d ", pre-1); pre=p[pre-1]; } printf("<-%d \n", v); } }
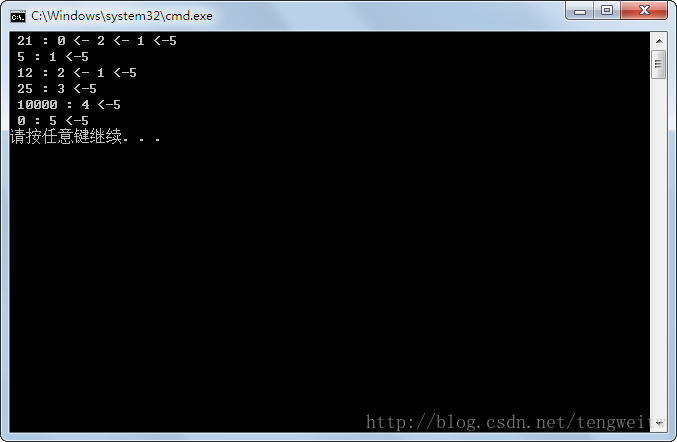
結果顯示如下:
注:如果程式出錯,可能是使用的開發平臺版本不同,請點選如下連結: 解釋說明
作者:nineheadedbird