二維陣列中的查詢 之 二分法
阿新 • • 發佈:2019-01-09
在一個二維陣列中,每一行都按照從左到右遞增的順序排序,每一列都按照從上到下遞增的順序排序。
請完成一個函式,輸入這樣的一個二維陣列和一個整數,判斷陣列中是否含有該整數。
例如下面的二維陣列就是每行、每列都遞增排序。如果在這個陣列中查詢數字7,則返回true;
如果查詢數字5,由於陣列不含有該數字,則返回false。
 我的解題思路是這樣的矩陣行列都是從小到大排好序的,要查詢的話自然用二分效率比較高,
而且這樣的矩陣有個性質,最左上角的元素必定是最小值,最右下角的是最大值,在一個
n*n的矩陣中,對角線的元素也是排好序的,找到對角線上的一個元素,使得這個元素小於
待查詢的key,並且下一元素大於待查詢的key,那麼只要在這個元素的左下角矩陣和右上角
矩陣遞迴繼續對角線查詢就可以了,例如上圖例子裡查詢7,只要找到對角線的元素4,然後
遞迴查詢紅圈的矩陣就可以了
我的解題思路是這樣的矩陣行列都是從小到大排好序的,要查詢的話自然用二分效率比較高,
而且這樣的矩陣有個性質,最左上角的元素必定是最小值,最右下角的是最大值,在一個
n*n的矩陣中,對角線的元素也是排好序的,找到對角線上的一個元素,使得這個元素小於
待查詢的key,並且下一元素大於待查詢的key,那麼只要在這個元素的左下角矩陣和右上角
矩陣遞迴繼續對角線查詢就可以了,例如上圖例子裡查詢7,只要找到對角線的元素4,然後
遞迴查詢紅圈的矩陣就可以了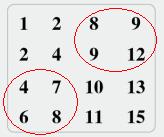 ,左上角矩陣最大值4<7,右下角
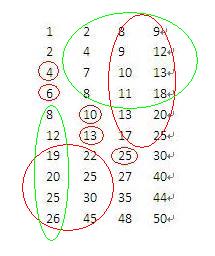
矩陣最小值10>7,無需查找了,但是此題並沒有告訴我們原始矩陣是n*n的,這是比較麻煩的
地方,不過思路是一樣的,無非不能用對角線查詢這樣簡單的辦法了,假設m*n的矩陣,對角線
查詢的辦法改進為i = (m1+m2)/2,j = (n1+n2)/2 進行查詢就可以了,(m1,n1)為矩陣最左上角
元素下標,(m2,n2)為最右下角元素下標
,左上角矩陣最大值4<7,右下角
矩陣最小值10>7,無需查找了,但是此題並沒有告訴我們原始矩陣是n*n的,這是比較麻煩的
地方,不過思路是一樣的,無非不能用對角線查詢這樣簡單的辦法了,假設m*n的矩陣,對角線
查詢的辦法改進為i = (m1+m2)/2,j = (n1+n2)/2 進行查詢就可以了,(m1,n1)為矩陣最左上角
元素下標,(m2,n2)為最右下角元素下標
{ int begin_m1 = m1, begin_n1 = n1, end_m2 = m2, end_n2 = n2;
int left_result = 0, right_result = 0;
int i = (m1+m2)/2, j = (n1+n2)/2; if (a == NULL) return 0;
if (value < *(a+m1*n+n1) || value > *(a+m2*n+n2))
return 0;
else if (value == *(a+m1*n+n1) || value == *(a+m2*n+n2))
return 1;
while ((i!=m1 || j!=n1) && (i!=m2 || j!=n2)){
if ( value == *(a+i*n+j) )
return 1;
else if ( value < *(a+i*n+j) ){
m2 = i;
n2 = j;
i = (i+m1)/2;
j = (j+n1)/2;
}
else{
m1 = i;
n1 = j;
i = (i+m2)/2;
j = (j+n2)/2;
}
}
//search left & right
if ( i<end_m2 )
left_result = binsearch(value, a, n, i+1, begin_n1, end_m2, j);
if ( j<end_n2 )
right_result = binsearch(value, a, n, begin_m1, j+1, i, end_n2);
if (left_result | right_result )
return 1; else
return 0;
}
 我的解題思路是這樣的矩陣行列都是從小到大排好序的,要查詢的話自然用二分效率比較高,
而且這樣的矩陣有個性質,最左上角的元素必定是最小值,最右下角的是最大值,在一個
n*n的矩陣中,對角線的元素也是排好序的,找到對角線上的一個元素,使得這個元素小於
待查詢的key,並且下一元素大於待查詢的key,那麼只要在這個元素的左下角矩陣和右上角
矩陣遞迴繼續對角線查詢就可以了,例如上圖例子裡查詢7,只要找到對角線的元素4,然後
遞迴查詢紅圈的矩陣就可以了
我的解題思路是這樣的矩陣行列都是從小到大排好序的,要查詢的話自然用二分效率比較高,
而且這樣的矩陣有個性質,最左上角的元素必定是最小值,最右下角的是最大值,在一個
n*n的矩陣中,對角線的元素也是排好序的,找到對角線上的一個元素,使得這個元素小於
待查詢的key,並且下一元素大於待查詢的key,那麼只要在這個元素的左下角矩陣和右上角
矩陣遞迴繼續對角線查詢就可以了,例如上圖例子裡查詢7,只要找到對角線的元素4,然後
遞迴查詢紅圈的矩陣就可以了 ,左上角矩陣最大值4<7,右下角
矩陣最小值10>7,無需查找了,但是此題並沒有告訴我們原始矩陣是n*n的,這是比較麻煩的
地方,不過思路是一樣的,無非不能用對角線查詢這樣簡單的辦法了,假設m*n的矩陣,對角線
查詢的辦法改進為i = (m1+m2)/2,j = (n1+n2)/2 進行查詢就可以了,(m1,n1)為矩陣最左上角
元素下標,(m2,n2)為最右下角元素下標
,左上角矩陣最大值4<7,右下角
矩陣最小值10>7,無需查找了,但是此題並沒有告訴我們原始矩陣是n*n的,這是比較麻煩的
地方,不過思路是一樣的,無非不能用對角線查詢這樣簡單的辦法了,假設m*n的矩陣,對角線
查詢的辦法改進為i = (m1+m2)/2,j = (n1+n2)/2 進行查詢就可以了,(m1,n1)為矩陣最左上角
元素下標,(m2,n2)為最右下角元素下標

{ int begin_m1 = m1, begin_n1 = n1, end_m2 = m2, end_n2 = n2;
int left_result = 0, right_result = 0;
int i = (m1+m2)/2, j = (n1+n2)/2; if (a == NULL) return 0;
if (value < *(a+m1*n+n1) || value > *(a+m2*n+n2))
return 0;
else if (value == *(a+m1*n+n1) || value == *(a+m2*n+n2))
return 1;
while ((i!=m1 || j!=n1) && (i!=m2 || j!=n2)){
if ( value == *(a+i*n+j) )
return 1;
else if ( value < *(a+i*n+j) ){
m2 = i;
n2 = j;
i = (i+m1)/2;
j = (j+n1)/2;
}
else{
m1 = i;
n1 = j;
i = (i+m2)/2;
j = (j+n2)/2;
}
}
//search left & right
if ( i<end_m2 )
left_result = binsearch(value, a, n, i+1, begin_n1, end_m2, j);
if ( j<end_n2 )
right_result = binsearch(value, a, n, begin_m1, j+1, i, end_n2);
if (left_result | right_result )
return 1; else
return 0;
}
