第二章、演算法基礎 -- 設計演算法
阿新 • • 發佈:2019-01-09
分治法
分治法:將原問題分解為幾個規模較小但類似於原問題的子問題,遞迴地求解這些子問題,然後再合併這些子問題的解來建立原問題的解。
分治模式在每層遞迴時都有三個步驟:
- 分解原問題為若干個子問題,這些子問題是原問題的規模較小的例項。
- 解決這些子問題,遞迴地求解各個子問題。然而,若子問題的規模足夠小,則直接求解。
- 合併這些子問題的解成原問題的解。
歸併排序
歸併排序完全遵循分治模式:
- 分解:分解待排序的n個元素的序列成各具個元素的兩個子序列。
- 解決:使用歸併排序遞迴地排序兩個子序列。
- 合併:合併兩個已排序的子序列以產生答案。
下圖是歸併排序排序一個數組的過程:

先自頂向下分解問題,再自底向上解決問題。
使用一個方法來合併已排序的子序列。虛擬碼:

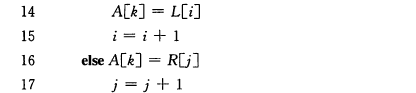
java程式碼實現:
private static void merge(int[] a, int p, int q, int r) { int[] left = new int[q - p + 1]; int[] right = new int[r - q]; for (int i = 0; i < left.length; i++) { left[i] = a[p + i]; } for (int j = 0; j < right.length; j++) { right[j] = a[q + j + 1]; } int i = 0, j = 0; while (p <= r) { if (left[i] <= right[j]) { a[p++] = left[i++]; if (i == left.length) { for (;j < right.length; j++) { a[p++] = right[j]; } break; } } else { a[p++] = right[j++]; if (j == right.length) { for (;i < left.length; i++) { a[p++] = left[i]; } break; } } } }
接下來把問題分解成子問題並遞迴呼叫演算法:
public static void sort(int[] a) { sort(a, 0, a.length - 1); } public static void sort(int[] a, int p, int r) { if (p < r) { int q = (p + r) / 2; sort(a, p, q); sort(a, q + 1, r); if (a[q] <= a[q + 1]) { return; } merge(a, p, q, r); } }
分析分治演算法
當一個演算法包含對其自身的遞迴呼叫時,我們往往可以用遞迴方程或遞迴式來描述其執行時間,該方程根據在較少輸入上的執行時間來描述在規模為n的問題上的總執行時間。
分治演算法執行時間的遞迴式來自基本模式的三個步驟。若問題規模足夠小,如對某個常量,,則直接求解需要常量時間。我們將其寫作。假設把原問題分解成個子問題,每個子問題的規模是原問題的。為了求解一個規模為
的子問題,需要,所以需要的時間來求解個子問題。如果分解問題成子問題需要時間,合併子問題的解為原問題的解需要時間,那麼得到遞迴式:
歸併排序演算法的分析
在歸併排序中,根據分治模式進行分析:
- 分解:分解步驟僅僅計運算元陣列的中間位置,需要常量時間,因此。
- 解決:我們遞迴地求解兩個規模均為n/2的子問題,將需要的執行時間。
- 合併:merge方法需要的時間,所以。
把跟相加後依舊是一個線性函式,即,相當於忽略掉每次分解需要的常數時間,給出歸併排序的最壞情況執行時間的遞迴式:
根據該遞迴式,可以得出歸併排序演算法的時間複雜度為,其推導過程如下:
可知 ,那麼,當時,
所以歸併排序演算法的時間複雜度為。
練習題

答:略

答:上面的java程式碼就是這樣實現。

答:
當時,,結論成立。
當時,我們假設結論成立,即。
如果時,結論也成立,那麼遞迴式的解就是。
根據遞迴式:
也就是當成立時,也成立。所以可以得出結論成立。

答:
計算其時間複雜度:
