歸併排序也是基本的排序之一，也挺重要的，所以寫這麼一篇部落格總結一下

歸併排序的一個特性是，它對N個元素的檔案排序所需要的時間與NlogN成正比，它的缺點是所需需要的空間和N成正比，要克服這個缺點的話，會造成程式碼非常複雜而且開銷巨大。所以如果速度不是主要的問題，而且有足夠的空間來使用，歸併排序是值得考慮的

歸併排序是一種穩定的方法，時間複雜度：T(n) = O(n㏒n)，空間複雜度：S(n) = O(n)

接下來看一下歸併排序到底如何實現

1.兩路歸併

如果給定兩個已經排好序的檔案，通過記錄下每個檔案中的最小元素，然後把兩個元素中最小的元素相比，小的那個移出輸出檔案，然後繼續迴圈直到兩個排好序的檔案的元素都已經輸出了，這樣就可以把他們簡單的組合為一個有序的檔案了

如圖就是一個標準的兩路歸併，程式碼如下：

void _MergeSort(int arr1[], int arr2[], int tmp[], int size1, int size2) {
	assert(arr1);
	assert(arr2);
	assert(tmp);
	int i = 0, j = 0, k = 0;
	for (; k < size1 + size2; ++k){
		if (i == size1) {
			/*表示陣列arr1已經歸完了*/
			tmp[k] = arr2[j++];
			continue;
		}
		if (j == size2) {
			tmp[k] = arr1[i++];
			continue;
		}
		/*把arr1和arr2中的元素進行歸併，歸入tmp陣列中*/
		if (arr1[i] < arr2[j]) {
			tmp[k] = arr1[i++];
		}
		else {
			tmp[k] = arr2[j++];
		}
	}
}
 

上面就是一種兩路歸併的程式碼，我們注意到，每次都需要判斷arr1和arr2是否已經歸併完畢，如果檔案太大的話，這是個不小的開銷

因為這兩個判斷通常為假，所以我們可以用設定觀察哨的方法，去掉測試操作，在陣列arr1和arr2的末尾放置一個比其他關鍵字都大的元素時，就可以去掉觀察哨了，因為當某個陣列訪問完畢的時候，該觀察哨可以讓另一個數組的元素繼續輸出直到整個陣列歸併完畢

然而，觀察哨並不那麼容易設定，難以確定觀察哨的最大值或者儲存空間不夠都是個問題，所以就有了下面的方法

2.抽象原位歸併

要複製陣列來執行原位歸併排序，只需要把第二個檔案變成倒序，這樣的安排使得兩個陣列中元素較大的元素自動成為了觀察哨，不論它在哪個數組裡面都可以

如圖：

我這裡沒畫具體的操作，就是兩個index，一個從左往右，一個從右往左，比較大小然後把較小的輸出，直到下標相等了結束複製操作，如此就得到一個有序的陣列，程式碼如下：

//抽象原位歸併,arr是已經構造好的bitonic序列
void MergeSort3(int arr[], int tmp[], int left, int mid, int right) {
	int i = 0, j = 0, k = 0;
	for (; i < mid; ++i) {
		tmp[i] = arr[i];
	}
	for (j = right; j >= mid; --j) {
		tmp[i++] = arr[j];
	}
	for (k = 0, i = 0, j = right; k <= right; ) {
		if (tmp[i] < tmp[j]) {
			arr[k++] = tmp[i++];
		}
		else {
			arr[k++] = tmp[j--];
		}
	}
}

注意，使用這種方法是不穩定的

好了，明白了上面的思路，我們來考慮一下如何對一個完全亂序的列表進行歸併排序而僅僅是對兩個有序的陣列排序

3.自頂向下的歸併排序

對一個數組進行歸併排序，把檔案分為兩部分，然後對兩部分遞迴的進行排序，接著將他們歸併,這種演算法是分治範型進行高效演算法設計的一個著名示例

程式碼如下：

void Merge(int arr[], int left, int mid, int right, int* tmp) {
	assert(arr);
	assert(tmp);
	int tmp_index = left;
	int cur1 = left;
	int cur2 = mid;
	while (cur1 < mid && cur2 < right) {
		if (arr[cur1] < arr[cur2]) {
			tmp[tmp_index++] = arr[cur1++];
		}
		else {
			tmp[tmp_index++] = arr[cur2++];
		}
	}
	while (cur1 < mid) {
		tmp[tmp_index++] = arr[cur1++];
	}
	while (cur2 < right) {
		tmp[tmp_index++] = arr[cur2++];
	}
	memcpy(arr + left, tmp + left, sizeof(int)*(right - left));
}

void _MergeSort(int arr[], int left, int right, int* tmp) {
	if (right - left <= 1) {
		//遞迴出口
		return;
	}
	int mid = left + (right - left) / 2;
	//對當前檔案進行劃分
	_MergeSort(arr, left, mid, tmp);
	_MergeSort(arr, mid, right, tmp);
	//遞迴的進行子檔案進行歸併 排序
	Merge(arr, left, mid, right, tmp);
}

void MergeSort(int arr[], int size) {
	assert(arr);
	//歸併排序，把兩個有序陣列，進行比較然後排序
	int* tmp = (int*)malloc(sizeof(arr)*size);
	_MergeSort(arr, 0, size, tmp);
	free(tmp);
}

4.基本演算法的改進

上面是對任意一個數組進行排序的程式碼，歸併排序是很理想的排序方法，執行時間與NlogN成正比，而且執行過程還具有穩定性，和在快速排序中討論的一樣，我們可以對小檔案進行處理來改進大多數遞迴演算法，所以，我們可以對小檔案進行插入排序來改進典型遞迴演算法，程式碼如下：

void _MergeSort(int arr[], int left, int right, int* tmp) {
	if (right - left <= 1) {
		//遞迴出口
		return;
	}
	//對較小的子檔案進行歸併排序
	if (right - left <= 3) {
		InsertSort(arr, left, right);
		return;
	}
	int mid = left + (right - left) / 2;
	_MergeSort(arr, left, mid, tmp);
	_MergeSort(arr, mid, right, tmp);
	Merge(arr, left, mid, right, tmp);
}

void MergeSort(int arr[], int size) {
	assert(arr);
	//歸併排序，把兩個有序陣列，進行比較然後排序
	int* tmp = (int*)malloc(sizeof(arr)*size);
	_MergeSort(arr, 0, size, tmp);
	free(tmp);
}

插入排序的程式碼如下：

void InsertSort(int arr[], int left, int right) {
	/*先設定一個觀察哨，把最小的元素放到陣列的開頭*/
	int i = 0;
	for (i = right - 1; i > left; --i) {
		if (arr[i - 1] > arr[i]) {
			Swap(&arr[i - 1], &arr[i]);
		}
	}
	/*然後再進行插入排序*/
	for (i = left + 2; i < right; ++i) {
		int j = i, value = arr[i];
		/*陣列的前兩個元素肯定是有序的*/
		while (value < arr[j - 1]) {
			//需要把前面的位置往後挪
			arr[j] = arr[j - 1];
			--j;
		}
		/*找到要插入的位置了*/
		arr[j] = value;
	}
}

每個遞迴程式都有一個等價的非遞迴程式與之對應，歸併排序有自頂向下的方法，也就有自底向上的方法

5.自底向上的歸併排序

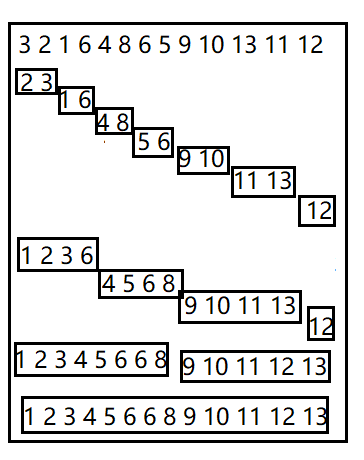
自底向上的策略是將其餘最小的檔案進行歸併，從陣列的左邊向右訪問，如圖

首先進行1-1合併，再進行2-2合併，一直往上，4-4合併，最後是8-5合併，排序的程式碼如下：

//前閉後開區間
void MergeSortByLoop(int arr[], int size) {
	assert(arr);
	assert(size > 0);
	int* tmp = (int*)malloc(sizeof(int)* size);
	int gap = 1;
	for (; gap < size; gap *= 2) {
		int i = 0;
		for (; i < size; i += 2 * gap) {
			int left = i;
			int mid = i + gap;
			int right = i + 2 * gap;
			if (mid > size) {
				mid = size;
			}
			if (right > size) {
				right = size;
			}
			Merge(arr, left, mid, right, tmp);
		}
	}
	free(tmp);
}

這裡定義一個gap變數，代表的是步長，gap從1開始，每次增加一倍，裡面的迴圈，是根據步長小序列每次進行歸併排序，但是要判斷mid和right是否到達邊界了，最後的歸併是gap-x的歸併，x小於等於步長gap。

自底向上和自頂向下歸併排序是兩種基於歸併的直接排序演算法，總結如上~

完