2. 程式人生 > >SVM支援向量機原理(二) 線性支援向量機的軟間隔最大化模型

SVM支援向量機原理(二) 線性支援向量機的軟間隔最大化模型

阿新 • • 發佈：2019-01-09

在支援向量機原理(一) 線性支援向量機中，我們對線性可分SVM的模型和損失函式優化做了總結。最後我們提到了有時候不能線性可分的原因是線性資料集裡面多了少量的異常點，由於這些異常點導致了資料集不能線性可分，本篇就對線性支援向量機如何處理這些異常點的原理方法做一個總結。

1. 線性分類SVM面臨的問題

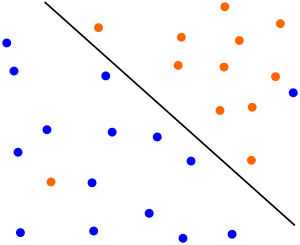
　　　　有時候本來資料的確是可分的，也就是說可以用 線性分類SVM的學習方法來求解，但是卻因為混入了異常點，導致不能線性可分，比如下圖，本來資料是可以按下面的實線來做超平面分離的，可以由於一個橙色和一個藍色的異常點導致我們沒法按照上一篇線性支援向量機中的方法來分類。

　　　　另外一種情況沒有這麼糟糕到不可分，但是會嚴重影響我們模型的泛化預測效果，比如下圖，本來如果我們不考慮異常點，SVM的超平面應該是下圖中的紅色線所示，但是由於有一個藍色的異常點，導致我們學習到的超平面是下圖中的粗虛線所示，這樣會嚴重影響我們的分類模型預測效果。

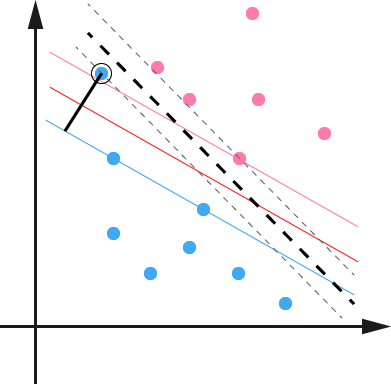
　　　　如何解決這些問題呢？SVM引入了軟間隔最大化的方法來解決。

2. 線性分類SVM的軟間隔最大化

　　　　所謂的軟間隔，是相對於硬間隔說的，我們可以認為上一篇線性分類SVM的學習方法屬於硬間隔最大化。

　　　　回顧下硬間隔最大化的條件：

min12||w|| 2 2 s.ty i (w T x i +b)≥1(i=1,2,...m) 

　　　　接著我們再看如何可以軟間隔最大化呢？

　　　　SVM對訓練集裡面的每個樣本(x i ,y i ) 引入了一個鬆弛變數ξ i ≥0 ,使函式間隔加上鬆弛變數大於等於1，也就是說：

y i (w∙x i +b)≥1−ξ i  

　　　　對比硬間隔最大化，可以看到我們對樣本到超平面的函式距離的要求放鬆了，之前是一定要大於等於1，現在只需要加上一個大於等於0的鬆弛變數能大於等於1就可以了。當然，鬆弛變數不能白加，這是有成本的，每一個鬆弛變數ξ

 i  , 對應了一個代價ξ i  ，這個就得到了我們的軟間隔最大化的SVM學習條件如下：

min12||w|| 2 2 +C∑ i=1 m ξ i   s.t.y i (w T x i +b)≥1−ξ i (i=1,2,...m)  ξ i ≥0(i=1,2,...m) 

　　　　這裡,C>0 為懲罰引數，可以理解為我們一般迴歸和分類問題正則化時候的引數。C 越大，對誤分類的懲罰越大，C 越小，對誤分類的懲罰越小。

　　　　也就是說，我們希望12||w|| 2 2  儘量小，誤分類的點儘可能的少。C是協調兩者關係的正則化懲罰係數。在實際應用中，需要調參來選擇。

　　　　這個目標函式的優化和上一篇的線性可分SVM的優化方式類似，我們下面就來看看怎麼對線性分類SVM的軟間隔最大化來進行學習優化。

3. 線性分類SVM的軟間隔最大化目標函式的優化

　　　　和線性可分SVM的優化方式類似，我們首先將軟間隔最大化的約束問題用拉格朗日函式轉化為無約束問題如下：

L(w,b,ξ,α,μ)=12||w|| 2 2 +C∑ i=1 m ξ i −∑ i=1 m α i [y i (w T x i +b)−1+ξ i ]−∑ i=1 m μ i ξ i  

　　　　其中 μ i ≥0,α i ≥0 ,均為拉格朗日系數。

　　　　也就是說，我們現在要優化的目標函式是：

min        w,b,ξ max        α i ≥0,μ i ≥0, L(w,b,α,ξ,μ) 

　　　　這個優化目標也滿足KKT條件，也就是說，我們可以通過拉格朗日對偶將我們的優化問題轉化為等價的對偶問題來求解如下：

max        α i ≥0,μ i ≥0, min        w,b,ξ L(w,b,α,ξ,μ) 

　　　　我們可以先求優化函式對於w,b,ξ 的極小值, 接著再求拉格朗日乘子α 和 μ 的極大值。

　　　　首先我們來求優化函式對於w,b,ξ 的極小值，這個可以通過求偏導數求得：

∂L∂w=0⇒w=∑ i=1 m 

相關推薦

SVM支援向量機原理(二) 線性支援向量機的軟間隔最大化模型

在支援向量機原理(一) 線性支援向量機中，我們對線性可分SVM的模型和損失函式優化做了總結。最後我們提到了有時候不能線性可分的原因是線性資料集裡面多了少量的異常點，由於這些異常點導致了資料集不能線性可分，本篇就對線性支援向量機如何處理這些異常點的原理方法做一個總結。 1

資料探勘十大演算法——支援向量機SVM（二）：線性支援向量機的軟間隔最大化模型

首先感謝“劉建平pinard”的淵博知識以及文中詳細準確的推導！！！ 支援向量機原理SVM系列文章共分為5部分： （一）線性支援向量機 （二）線性支援向量機的軟間隔最大化模型 （三）線性不可分支援向量機與核函式 （四）SMO演算法原理 （五）線性支援迴歸

支援向量機SVM（二）：基於軟間隔最大化的線性SVM

前言 由上節，線性可分SVM的學習模型為 min⁡ω,b12∣∣ω∣∣2s.t.1−yi(ω⋅xi+b)≤0\begin{aligned} \min_{\bm\omega, b} &\quad\frac{1}{2}||\bm\omega|

詳解SVM系列（四）：線性支援向量機與軟間隔最大化

線性支援向量機 線性可分問題的支援向量機學習方法，對線性不可分訓練資料是不適用的，因為這時上述方法的不等式約束並不能都成立。 舉2個例子： 如果沒有混入異常點，導致不能線性可分，則資料可以按上面的實線來做超平面分離的。 這種情況雖然不是不可分的，但是由於其中的一個藍色點不滿足線性

(3).支援向量機SVM——軟間隔最大化公式手寫詳細推導

線性可分問題的支援向量機學習方法，對線性不可分訓練資料是不適應的，因為這時上一節中不等式約束不能成立，如何擴充套件到線性不可分問題呢？這就需要修改硬間隔最大化，使其成為軟間隔最大化。 通常情況下訓練資料中有一些特異的點，將這些特異的點去處後，剩下的樣本組成的集合是線性可分的。線性不可分的意思

支援向量機（二）——深入理解最優間隔分類器

1. 最優間隔分類器理論 之前我們提到在支援向量機中，我們的目標是尋找一個超平面，使得離超平面比較近的點能有更大的間距，也就是說我們不必考慮所有的點都必須遠離超平面，我們關心求得的超平面能夠讓所有點中離它最近的點有最大間距。 因此，注意最優間隔分類器我們的任

支援向量機2—線性支援向量機與軟間隔最大化

1、線性支援向量機線性可分問題的支援向量機學習方法，對線性不可分訓練資料是不適用的。因為這時上述方法中的不等式約束並不能都成立。這時就需要修改硬間隔最大化，使其成為軟間隔最大化。假設給定一個特徵空間上的訓練資料集T={（x1,y1），（x2,y2），...，（xN,yN）}，

SVM 支援向量機(2) 軟間隔最大化與核方法

對於某些資料集, 並不能找到一個超平面把它們分開, 也就是說不能找到一組w⃗ ,b, 滿足yi(w⃗ ⋅x⃗ i+b)≥1, 解決辦法就是引入一個鬆弛變數ξi, 讓所有樣本點都滿足yi(w⃗ ⋅x⃗ i+b)≥1−ξi, 這樣得到一個新的約束條件, 可以注意到ξ

線性可分支持向量機與軟間隔最大化

技術分享 最大化 bubuko 線性 分支 inf http bsp 9.png 線性可分支持向量機與軟間隔最大化

SVM中的軟間隔最大化與硬間隔最大化

參考文獻：https://blog.csdn.net/Dominic_S/article/details/83002153 1.硬間隔最大化     對於以上的KKT條件可以看出，對於任意的訓練樣本總有ai=0或者yif(xi) - 1=0即yif(xi) = 11）當ai=0

SVM——軟間隔最大化

回憶SVM硬間隔最大化所對應的優化問題 minw,b12∥w∥2s.t.y(i)(wTx(i)+b)⩾1i=1,⋯,mminw,b12‖w‖2s.t.y(i)(wTx(i)+b)⩾1i=1,⋯,m 對於約束條件，並不是所有樣本都能滿足，換句話說，可能存在某個

機器學習：SVM（一）——線性可分支援向量機原理與公式推導

原理 SVM基本模型是定義在特徵空間上的二分類線性分類器（可推廣為多分類），學習策略為間隔最大化，可形式化為一個求解凸二次規劃問題，也等價於正則化的合頁損失函式的最小化問題。求解演算法為序列最小最優化演算法（SMO） 當資料集線性可分時，通過硬間隔最大化，學習一個線性分類器；資料集近似線性可分時，即存在一小

TensorFlow深度學習框架學習（二）：TensorFlow實現線性支援向量機（SVM）

SVM的原理可以參考李航的《統計學習方法》 具體程式碼如下，程式碼都有註釋的 #1、匯入必要的庫 import matplotlib.pyplot as plt import numpy as np import tensorflow as tf fro

分類演算法----線性可分支援向量機（SVM）演算法的原理推導

支援向量機（support vector machines, SVM）是一種二分類模型，它的基本模型是定義在特徵空間上的間隔最大的線性分類器， 其目標是在特徵空間中找到一個分離超平面，能將例項分到不同的類，分離超平面將特徵空間劃分為兩部分，正類和負類，法向量 指向的為正類，

詳解SVM系列（三）：線性可分支援向量機與硬間隔最大化

支援向量機概覽（support vector machines SVM） 支援向量機是一種二類分類模型。它的基本模型是定義在特徵空間上的間隔最大（間隔最大區別於感知機）線性分類器（核函式可以用非線性的分類）。 支援向量機的學習策略是間隔最大化可形式化為一個求解凸二次規劃的問題。 也等

SVM支援向量機系列理論（七） 線性支援向量機與L2正則化 Platt模型

7.1 軟間隔SVM等價於最小化L2正則的合頁損失 上一篇 說到， ξi ξ i \xi_i 表示偏離邊界的度量，若樣本點

【機器學習】最小二乘法支援向量機LSSVM的數學原理與Python實現

【機器學習】最小二乘法支援向量機LSSVM的數學原理與Python實現 一、LSSVM數學原理 1. 感知機 2. SVM 3. LSSVM 4. LSSVM與SVM的區別 二、LSSVM的py

05 SVM - 支援向量機 - 概念、線性可分

一、SVM概念 支援向量機(Support Vector Machine, SVM)本身是一個__二元分類演算法__，是對感知器演算法模型的一種擴充套件，現在的SVM演算法支援__線性分類__和__非線性分類__的分類應用，並且也能夠直接將SVM應用於__迴歸應用__中，同時通過OvR或者OvO

資料探勘十大演算法——支援向量機SVM（一）：線性支援向量機

首先感謝“劉建平pinard”的淵博知識以及文中詳細準確的推導！！！ 本文轉自“劉建平pinard”，原網址為：http://www.cnblogs.com/pinard/p/6097604.html。 支援向量機原理SVM系列文章共分為5部分： （一）線性支援向量機

支援向量機原理（理解SVM的三層境界）

 支援向量機通俗導論（理解SVM的三層境界） 作者：July 。致謝：pluskid、白石、JerryLead。 說明：本文最初寫於2012年6月，而後不斷反反覆覆修改&優化，修改次數達上百次，最後修改於2016年11月。 宣告：