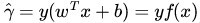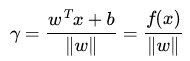支援向量機原理(理解SVM的三層境界)
作者:July 。致謝:pluskid、白石、JerryLead。支援向量機通俗導論(理解SVM的三層境界)
說明:本文最初寫於2012年6月,而後不斷反反覆覆修改&優化,修改次數達上百次,最後修改於2016年11月。
宣告:本文於2012年便早已附上所有參考連結,並註明是篇“學習筆記”,且寫明具體參考了pluskid等人的文章。文末2013年的PDF是為證。
前言
動筆寫這個支援向量機(support vector machine)是費了不少勁和困難的,原因很簡單,一者這個東西本身就並不好懂,要深入學習和研究下去需花費不少時間和精力,二者這個東西也不好講清楚,儘管網上已經有朋友寫得不錯了(見文末參考連結
本文在寫的過程中,參考了不少資料,包括《支援向量機導論》、《統計學習方法》及網友pluskid的支援向量機系列等等,於此,還是一篇學習筆記,只是加入了自己的理解和總結,有任何不妥之處,還望海涵。全文巨集觀上整體認識支援向量機的概念和用處,微觀上深究部分定理的來龍去脈,證明及原理細節,力保邏輯清晰 & 通俗易懂。
同時,閱讀本文時建議大家儘量使用chrome等瀏覽器,如此公式才能更好的顯示,再者,閱讀時可拿張紙和筆出來,把本文所有定理.公式都親自推導一遍或者直接列印下來(可直接列印網頁版或本文文末附的PDF)
OK,還是那句話,有任何問題,歡迎任何人隨時不吝指正 & 賜教,感謝。
第一層、瞭解SVM
支援向量機,因其英文名為support vector machine,故一般簡稱SVM,通俗來講,它是一種二類分類模型,其基本模型定義為特徵空間上的間隔最大的線性分類器,其學習策略便是間隔最大化,最終可轉化為一個凸二次規劃問題的求解。
1.1、分類標準的起源:Logistic迴歸
理解SVM,咱們必須先弄清楚一個概念:線性分類器。
給定一些資料點,它們分別屬於兩個不同的類,現在要找到一個線性分類器把這些資料分成兩類。如果用x
可能有讀者對類別取1或-1有疑問,事實上,這個1或-1的分類標準起源於logistic迴歸。
Logistic迴歸目的是從特徵學習出一個0/1分類模型,而這個模型是將特性的線性組合作為自變數,由於自變數的取值範圍是負無窮到正無窮。因此,使用logistic函式(或稱作sigmoid函式)將自變數對映到(0,1)上,對映後的值被認為是屬於y=1的概率。
假設函式
其中x是n維特徵向量,函式g就是logistic函式。 而
 的影象是
的影象是
可以看到,將無窮對映到了(0,1)。 而假設函式就是特徵屬於y=1的概率。
從而,當我們要判別一個新來的特徵屬於哪個類時,只需求 即可,若
即可,若 大於0.5就是y=1的類,反之屬於y=0類。
大於0.5就是y=1的類,反之屬於y=0類。
此外, 只和
只和 有關,
有關, >0,那麼
>0,那麼 ,而g(z)只是用來對映,真實的類別決定權還是在於
,而g(z)只是用來對映,真實的類別決定權還是在於 。再者,當
。再者,當 時,
時, =1,反之
=1,反之 =0。如果我們只從
=0。如果我們只從 出發,希望模型達到的目標就是讓訓練資料中y=1的特徵
出發,希望模型達到的目標就是讓訓練資料中y=1的特徵 ,而是y=0的特徵
,而是y=0的特徵 。Logistic迴歸就是要學習得到
。Logistic迴歸就是要學習得到 ,使得正例的特徵遠大於0,負例的特徵遠小於0,而且要在全部訓練例項上達到這個目標。
,使得正例的特徵遠大於0,負例的特徵遠小於0,而且要在全部訓練例項上達到這個目標。
接下來,嘗試把logistic迴歸做個變形。首先,將使用的結果標籤y = 0和y = 1替換為y = -1,y = 1,然後將 (
( )中的
)中的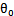
 替換為
替換為 (即
(即 )。如此,則有了
)。如此,則有了 。也就是說除了y由y=0變為y=-1外,線性分類函式跟logistic迴歸的形式化表示
。也就是說除了y由y=0變為y=-1外,線性分類函式跟logistic迴歸的形式化表示 沒區別。
沒區別。
進一步,可以將假設函式 中的g(z)做一個簡化,將其簡單對映到y=-1和y=1上。對映關係如下:
中的g(z)做一個簡化,將其簡單對映到y=-1和y=1上。對映關係如下:
1.2、線性分類的一個例子
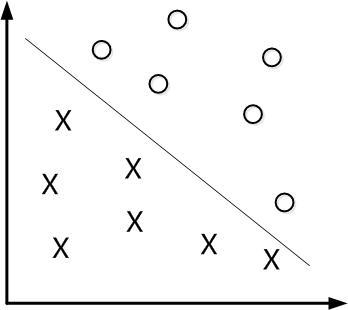
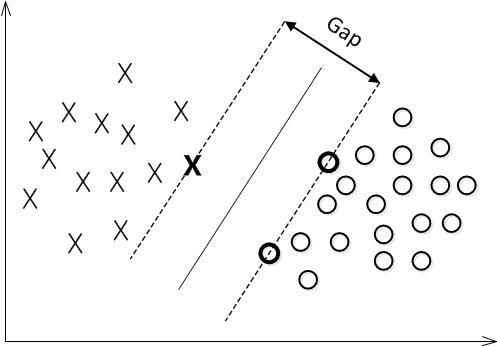
下面舉個簡單的例子。如下圖所示,現在有一個二維平面,平面上有兩種不同的資料,分別用圈和叉表示。由於這些資料是線性可分的,所以可以用一條直線將這兩類資料分開,這條直線就相當於一個超平面,超平面一邊的資料點所對應的y全是-1 ,另一邊所對應的y全是1。
這個超平面可以用分類函式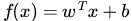
注:有的資料上定義特徵到結果的輸出函式
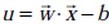 ,與這裡定義的
,與這裡定義的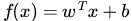 實質是一樣的。為什麼?因為無論是
實質是一樣的。為什麼?因為無論是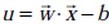 ,還是
,還是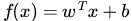 ,不影響最終優化結果。下文你將看到,當我們轉化到優化
,不影響最終優化結果。下文你將看到,當我們轉化到優化
(有一朋友飛狗來自Mare_Desiderii,看了上面的定義之後,問道:請教一下SVM functional margin 為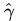
換言之,在進行分類的時候,遇到一個新的資料點x,將x代入f(x) 中,如果f(x)小於0則將x的類別賦為-1,如果f(x)大於0則將x的類別賦為1。
接下來的問題是,如何確定這個超平面呢?從直觀上而言,這個超平面應該是最適合分開兩類資料的直線。而判定“最適合”的標準就是這條直線離直線兩邊的資料的間隔最大。所以,得尋找有著最大間隔的超平面。
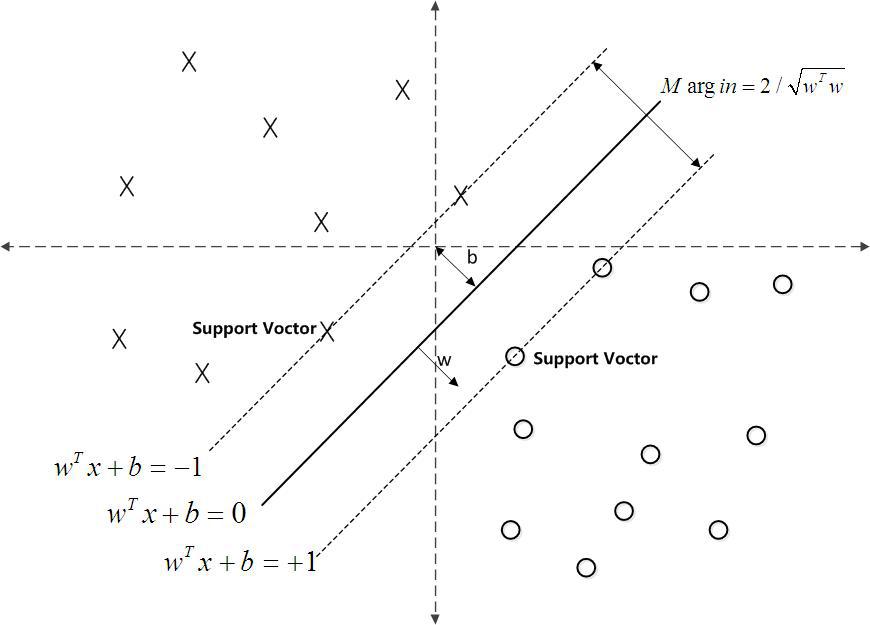
1.3、函式間隔Functional margin與幾何間隔Geometrical margin
在超平面w*x+b=0確定的情況下,|w*x+b|能夠表示點x到距離超平面的遠近,而通過觀察w*x+b的符號與類標記y的符號是否一致可判斷分類是否正確,所以,可以用(y*(w*x+b))的正負性來判定或表示分類的正確性。於此,我們便引出了函式間隔(functional margin)的概念。
定義函式間隔(用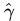
而超平面(w,b)關於T中所有樣本點(xi,yi)的函式間隔最小值(其中,x是特徵,y是結果標籤,i表示第i個樣本),便為超平面(w, b)關於訓練資料集T的函式間隔:
= min
i (i=1,...n)
但這樣定義的函式間隔有問題,即如果成比例的改變w和b(如將它們改成2w和2b),則函式間隔的值f(x)卻變成了原來的2倍(雖然此時超平面沒有改變),所以只有函式間隔還遠遠不夠。
事實上,我們可以對法向量w加些約束條件,從而引出真正定義點到超平面的距離--幾何間隔(geometrical margin)的概念。
假定對於一個點 x ,令其垂直投影到超平面上的對應點為 x0 ,w 是垂直於超平面的一個向量,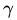
根據平面幾何知識,有
其中||w||為w的二階範數(範數是一個類似於模的表示長度的概念),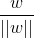
又由於 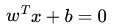
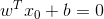
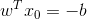
隨即讓此式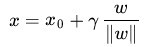
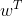
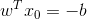
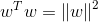
為了得到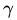
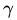
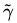
從上述函式間隔和幾何間隔的定義可以看出:幾何間隔就是函式間隔除以||w||,而且函式間隔y*(wx+b) = y*f(x)實際上就是|f(x)|,只是人為定義的一個間隔度量,而幾何間隔|f(x)|/||w||才是直觀上的點到超平面的距離。
1.4、最大間隔分類器Maximum Margin Classifier的定義
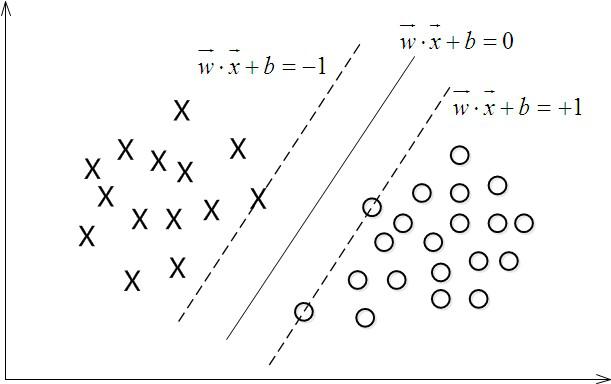
對一個數據點進行分類,當超平面離資料點的“間隔”越大,分類的確信度(confidence)也越大。所以,為了使得分類的確信度儘量高,需要讓所選擇的超平面能夠最大化這個“間隔”值。這個間隔就是下圖中的Gap的一半。
通過由前面的分析可知:函式間隔不適合用來最大化間隔值,因為在超平面固定以後,可以等比例地縮放w的長度和b的值,這樣可以使得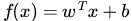
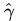
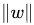
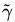
於是最大間隔分類器(maximum margin classifier)的目標函式可以定義為:
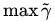
同時需滿足一些條件,根據間隔的定義,有
其中,s.t.,即subject to的意思,它匯出的是約束條件。
回顧下幾何間隔的定義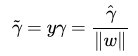
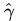
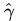
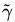
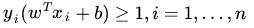
相當於在相應的約束條件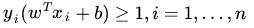
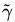
如下圖所示,中間的實線便是尋找到的最優超平面(Optimal Hyper Plane),其到兩條虛線邊界的距離相等,這個距離便是幾何間隔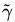
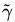
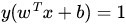
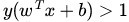
OK,到此為止,算是瞭解到了SVM的第一層,對於那些只關心怎麼用SVM的朋友便已足夠,不必再更進一層深究其更深的原理。
1.5、令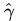 等於1的原因分析:
等於1的原因分析:
如下為函式間隔:
兩邊同時除以 ,(前提線性可分的,所有一定存在一個超平面,也就意味著
)
於是我們得到:
令: