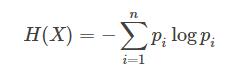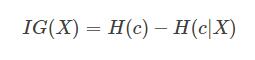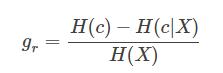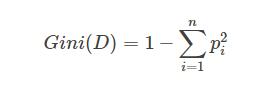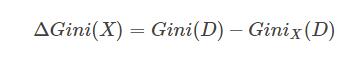【演算法】決策樹,資訊熵,資訊增益,Gini
決策樹演算法中,ID3使用資訊增益(選大的),C4.5使用資訊增益比(選大的),CART使用Gini(選小的)。
決策樹是通過一系列規則對資料進行分類的過程。它提供一種在什麼條件下會得到什麼值的類似規則的方法。
決策樹分為分類樹和迴歸樹兩種,分類樹對離散變數做決策樹,迴歸樹對連續變數做決策樹。
一棵決策樹的生成過程主要分為以下3個部分:
1、特徵選擇:特徵選擇是指從訓練資料中眾多的特徵中選擇一個特徵作為當前節點的分裂標準,如何選擇特徵有著很多不同量化評估標準標準,從而
衍生出不同的決策樹演算法。
2、決策樹生成: 根據選擇的特徵評估標準,從上至下遞迴地生成子節點,直到資料集不可分則停止決策樹停止生長。 樹結構來說,遞迴結構是最容
易理解的方式。
3、剪枝:決策樹容易過擬合,一般來需要剪枝,縮小樹結構規模、緩解過擬合。剪枝技術有預剪枝和後剪枝兩種。
決策樹適用於數值型和標稱型(離散型資料,變數的結果只在有限目標集中取值),能夠讀取資料集合,提取一些列資料中蘊含的規則。在分類問題中
使用決策樹模型有很多的優點,決策樹計算複雜度不高、便於使用、而且高效,決策樹可處理具有不相關特徵的資料、可很容易地構造出易於理解的規
則,而規則通常易於解釋和理解。
決策樹模型也有一些缺點,比如處理缺失資料時的困難、過度擬合以及忽略資料集中屬性之間的相關性等。
分類與迴歸樹(CART——Classification And Regression Tree):二元分裂
霍夫曼編碼:利用大概率事件分配短碼的思想。
--------------------------------------------------------------------------------------------
一個事件的資訊量就是這個事件發生的概率的負對數。
資訊熵:平均而言發生一個事件我們得到的資訊量大小。所以數學上,資訊熵其實是資訊量的期望。
特徵X的熵:
熵:表示隨機變數的不確定性。變數不確定性越高,熵越高。
--------------------------------------------------------------------------------------------
條件熵:在一個條件下,隨機變數的不確定性。
資訊增益:熵 - 條件熵,在一個條件下,資訊不確定性減少的程度。
特徵X的資訊增益 :資訊增益 = entroy(前) - entroy(後)
資訊增益比為:
--------------------------------------------------------------------------------------------
Gini係數是一種與資訊熵類似的做特徵選擇的方式,可以用來資料的不純度。
在CART演算法中, 基尼不純度表示一個隨機選中的樣本在子集中被分錯的可能性。
基尼不純度為這個樣本被選中的概率乘以它被分錯的概率。
當一個節點中所有樣本都是一個類時,基尼不純度為零。
假設y的可能取值為{1, 2, ..., m},令fi是樣本被賦予i的概率,則基尼指數可以通過如下計算:CART演算法中的基尼指數:
在CART(Classification and Regression Tree)演算法中利用基尼指數構造二叉決策樹。
Gini係數的計算方式如下:
其中,D表示資料集全體樣本,pi表示每種類別出現的概率。
取個極端情況,如果資料集中所有的樣本都為同一類,那麼有p0=1,Gini(D)=0,顯然此時資料的不純度最低。
與資訊增益類似,我們可以計算如下表達式:
上面式子表述的意思就是,加入特徵X以後,資料不純度減小的程度。
在做特徵選擇的時候,我們可以取ΔGini(X)最大的那個