樹狀陣列定義

樹狀陣列陣列顧名思義它是樹狀的陣列
百度：樹狀陣列(Binary Indexed Tree(B.I.T), Fenwick Tree)是一個查詢和修改複雜度都為log(n)的資料結構。

樹狀陣列常用操作

一、神奇的lowbit

假設陣列a[1…n]，那麼查詢a[1]+…+a[n]的時間是log級別的，而且是一個線上的資料結構，支援隨時修改某個元素的值，複雜度也為log級別。
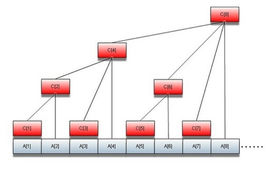
來觀察這個圖：
令這棵樹的結點編號為C1，C2…Cn。令每個結點的值為這棵樹的值的總和，那麼容易發現：
C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
…
C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16

那麼就有了一個有趣的性質

設節點編號為x，那麼這個節點管轄的區間為2^k（其中k為x二進位制末尾0的個數）個元素。因為這個區間最後一個元素必然為Ax，
所以很明顯：Cn = A(n – 2^k + 1) + … + An

那麼lowbit操作就顯而易見了

inline int lowbit(int k) {
	return k & -k;
}

二、單點修改

由於在樹狀陣列中改變一個點會牽動所有管轄他的店那麼在修改時就需要lowbit了

inline void add(int x, int k) { //x要修改的那個數， k為要加的值
	while(x <= n) {
		c[x] += k;
		x += lowbit(x);
	}
}
 

三、求和操作

inline int ask(int k) {
	int ans = 0;
	while(k) {
		ans += s[k];
		k -= lowbit(k);
	}
}