一、二叉排序樹

對於無序的序列“62，58，88，47，73，99，35，51，93，29，37，49，56，36，48，50”，是否存在一種高效的查詢方案，使得能夠快速判斷在序列中是否存在指定的數值？二叉排序樹是一種簡單，高效的資料結構。

二叉排序樹，又稱為二叉查詢樹。二叉排序樹或者是一棵空樹，或者是具有以下性質的二叉樹：若其左子樹不為空，則左子樹上的所有節點的值均小於它的根結點的值；若其右子樹不為空，則右子樹上的所有節點的值均大於它的根結點的值；左右子樹又分別是二叉排序樹。

對於以上的序列，我們構建如下的二叉排序樹，其左子樹小於根結點的值，右子樹大於根結點的值：

二、二叉排序樹的基本操作

二叉排序樹的結構為：

typedef struct tree_node{
        double value;
        struct tree_node *left;
        struct tree_node *right;
}*node, binode;

在二叉排序樹中，其最主要的特點是其左子樹小於其根結點的值，右子樹大於根結點的值。

1、查詢

二叉排序樹的查詢是指在二叉排序樹中查詢到對應的值，如在上述的二叉排序樹中查詢“49”，其具體過程為：

• 與根結點的值相比：49<52，查詢其左子樹
• 49<58，查詢其左子樹
• 49>47，查詢其右子樹
• 49<51，查詢其左子樹
• 49=49，查詢成功

其具體過程如下圖所示：

其具體實現過程為：

int search_value(node root, double a, node *p){
        if (NULL == root) {
                return 1; // 查詢不成功
        }
        else if (a == root->value) {
                return 0; // 樹中已經存在該節點
        }else if (a < root->value) {
                *
 
p = root; // 記錄父節點
                return search_value(root->left, a, p); //查詢左子樹
        }else {
                *p = root;
                return search_value(root->right, a, p); // 查詢右子樹
        }
}

2、插入

對於插入操作，主要分為兩種情況：

• 若二叉排序樹中存在該值，則不做任何操作
• 若二叉排序樹中不存在該值，則插入

插入的具體操作是判斷與二叉排序樹中節點的值，若小於當前節點的值，則選擇左子樹插入，若大於當前節點的值，則選擇右子樹插入；對於左右子樹，進行同樣的操作。

其實現過程為：

int insert_tree(node *root, double a){
        node p = *root;
        node q = NULL;
        printf("insert: %lf\n", a);

        if (search_value(*root, a, &p) == 1) { // 查詢樹中是否存在a
                q = (binode *)malloc(sizeof(binode)); // 不存在a，申請空間
                q->value = a;
                q->left = q->right = NULL;

                if (*root == NULL){ // 樹為空
                        *root = q;
                }else {
                        if (a < p->value){
                                p->left = q; // 插入左子樹
                        }else{
                                p->right = q; // 插入右子樹
                        }
                }
                return 0;
        }
        return 1;
}

3、刪除

二叉排序樹中節點的刪除操作相比其他的操作就比較複雜一點，首先，通過查詢二叉排序樹中是否存在節點，若存在，主要分為如下的三種情況：

• 節點既無左子樹，又無右子樹

刪除的方法：設定父節點指向該節點的指標為空，直接刪除該節點。如刪除值為“50”的節點：

• 若刪除的節點只包含左子樹或者只包含右子樹

刪除的方法：刪除該節點，以其左子樹或者右子樹代替該節點。如刪除值為“58”的節點：

• 若刪除的節點既包含左子樹，又包含右子樹

刪除的方法：

• 找到待刪除的節點，選擇其左子樹中的最大的節點或者其右子樹中最小的節點，這裡選擇左子樹中最大的節點，以刪除值為“47”的節點為例：

• 在左子樹中找到最大的節點，根據二叉排序樹的特點，值最大的節點要麼是根結點（無右子樹），要麼是最右的節點，在這裡，其左子樹中最大的節點為“37”，以該節點替換需要刪除的節點，即以“37”替換節點“47”，再將該節點的左子樹作為其父節點的右子樹，即將“36”作為“35”的右子樹：

其具體的過程為：

int delete_node(node *root, double a){
        // 判斷樹中書否存在a
        node p = *root;
        if (search_value(*root, a, &p) == 0){// 存在該節點
                // 開始刪除,p指向的刪除節點的父節點
                node q = NULL;// q指向要刪除的節點
                if (a < p->value){
                        q = p->left;
                }else{
                        q = p->right;
                }

                if (q->left == NULL && q->right == NULL){ //葉子節點，直接刪除
                        if (a < p->value) p->left = NULL;
                        else p->right = NULL;
                }else if ((q->left == NULL && q->right != NULL) || (q->left != NULL && q->right == NULL)){
                        // 只有左子樹或者只有右子樹
                        node r = (q->left == NULL ? q->right : q->left); // 指向q不為空的子樹
                        if (a < p->value) p->left = r;
                        else p->right = r;
                }else{ // 既有左子樹又有右子樹
                        // 這裡選擇左子樹最大的節點作為父節點
                        node r = q->left;
                        // 判斷r的右子樹是否為空
                        if (r->right == NULL){ // 右子樹為空
                                p->left = r;
                                r->right = q->right;
                        }else{ // 右子樹不為空
                                node r1 = r;
                                node r1_father = r;
                                // 尋找最右子樹
                                while (r1->right != NULL){
                                        r1_father = r1;
                                        r1 = r1->right;
                                }
                                // 此時r1不可能存在右子樹
                                r1_father->right = r1->left;
                                r1->left = r;
                                r1->right = q->right;
                                p->left = r1;
                        }
                }
                free(q);
                q = NULL;
                return 0;

        }
        return 1;
}

4、中序遍歷

對於二叉排序樹，其中序遍歷的輸出結果正好是排好序的序列，其中序

void in_order(node root){
        node p = root;
        if (p != NULL){
                in_order(p->left);
                fprintf(stderr, "%lf\n", p->value);
                in_order(p->right);
        }
}

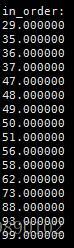
對於上述的序列“62，58，88，47，73，99，35，51，93，29，37，49，56，36，48，50”其中序遍歷的結果為：

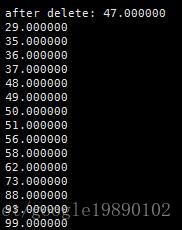
刪除“47”後的中序遍歷的結果為：

參考文獻

• 《大話資料結構》
• 《資料結構》(C語言版)