特徵值分解與奇異值分解及其應用

阿新 • • 發佈：2019-01-09

SVD奇異值分解

正交矩陣

正交矩陣

正交矩陣對應著正交變換，特點在於不改變向量的尺寸（模）和任意兩個向量的夾角。在x-y座標系中，通俗地講，就是旋轉兩個座標軸，得到新的互相垂直的座標軸，求向量在新座標系中的投影。

正交變換舉例

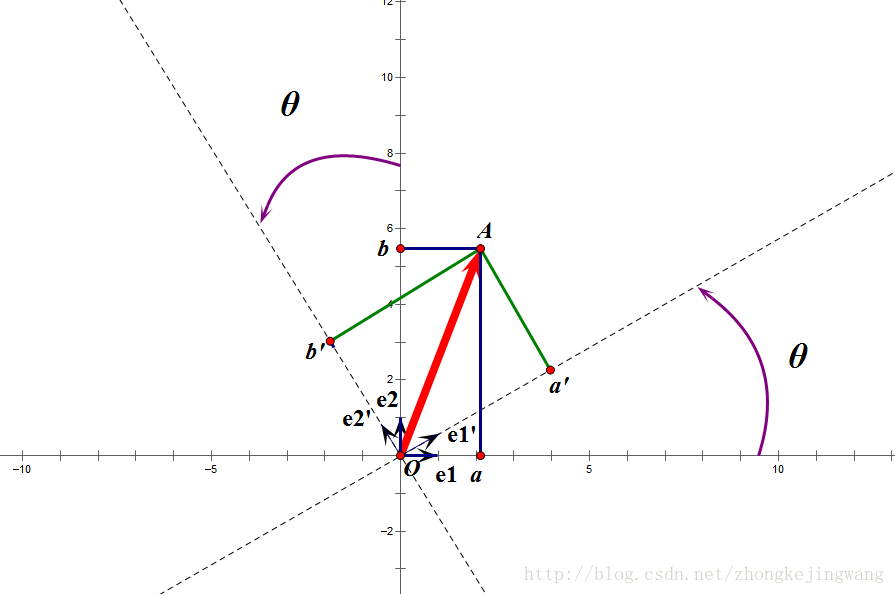
圖片摘自此處。例如向量 $OA$ ，在原始 $e_{1} -$

e2" role="presentation" style="position: relative;">

e_{1} - e_{2}

$e_1-e_2$ 座標系中表示為

(a, b)^{T}

$(a,b)^T$ ，在旋轉後的座標系

e_{1}^{'} - e_{2}^{'}

$e_1'-e_2'$ 中表示為

(a^{'}, b^{'})^{T}

$(a',b')^T$ ，若存在一個矩陣

U

$U$ 使得

(a^{'}, b^{'})^{T} = U (a, b)^{T}

$(a',b')^T=U(a,b)^T$ ，則矩陣

U

$U$ 是正交矩陣（可見對應著座標系之間的正交變換）。
可以代入求得矩陣

U

$U$ ，且可觀察到矩陣的行向量之間都是正交的，列向量之間也是正交的。

U = [\begin{matrix} \cos θ & \sin θ \\ - \sin θ & \cos θ \end{matrix}]

$U=\left[\begin{matrix}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{matrix}\right]$

正交矩陣的性質

正交陣的逆等於其轉置

A^{T} A = I \to A^{T} = A^{- 1}

$A^TA=I\rightarrow A^T=A^{-1}$

特徵值分解

特徵值分解

$A$ 是 $N\times N$ 滿秩對稱方陣（對稱陣的特徵向量之間兩兩正交），有 $N$ 個特徵值 $\lambda_i$ ，對應 $N$ 個特徵向量 $q_i$ ，有：

{\begin{matrix} A q_{1} = λ_{1} q_{1} \\ A q_{2} = λ_{2} q_{2} \\ \dots \\ A q_{N} = λ_{N} q_{N} \end{matrix}

$\left \{ \begin{matrix} Aq_1=\lambda_1q_1 \\ Aq_2=\lambda_2q_2 \\ \cdots \\ Aq_N=\lambda_Nq_N \end{matrix}\right .$
可以理解為向量

q_{i}

$q_i$ 在

A

$A$ 的作用下，保持方向不變，只進行比例為

λ_{i}

$\lambda_i$ 的縮放。特徵向量所在的直線包含了所有特徵向量（稱為特徵空間）。
以上

N

$N$ 個等式寫成矩陣形式（

q_{i}

$q_i$ 是

N \times 1

$N\times 1$ 的列向量！）

A [q_{1}, q_{2}, \dots, q_{N}] = [q_{1}, q_{2}, \dots, q_{N}] [\begin{matrix} λ_{1} & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & λ_{N} \end{matrix}] A Q = Q Λ

$A[q_1,q_2,\cdots,q_N]=[q_1,q_2,\cdots,q_N]\left [\begin{matrix} \lambda_1 & \cdots & 0\\ \vdots &\ddots & \vdots \\0 & \cdots & \lambda_N \end{matrix} \right ]\\ AQ=Q\Lambda$
等式兩邊右乘

Q

$Q$ 的逆，得到

A

$A$ 的特徵值分解：

A = Q Λ Q^{- 1}

$A=Q\Lambda Q^{-1}$
進一步，由於特徵向量矩陣

Q

$Q$ 各列相互正交，所以

Q

$Q$ 是正交陣，正交陣的逆等於其轉置:

A = Q Λ Q^{T}

$A=Q\Lambda Q^T$

A = [q_{1}, q_{2}, \dots, q_{N}] [