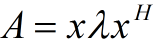1、首先，矩陣可以認為是一種線性變換：確定了定義域空間與目標空間的兩組基，就可以很自然地得到該線性變換的矩陣表示。即矩陣A可以通過Ax=b將一個向量x線性變換到另一個向量b，這個過程中，線性變換的作用包含三類效應：旋轉、縮放和投影。

2、奇異值分解體現了對線性變換這三種效用的一個析構。
在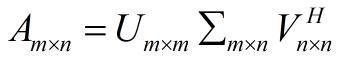中，U的列向量組成了一組標準正交基，V的列向量也是，這表示我們找到了U和V這兩組基，A矩陣的作用是將一個向量從V這組正交基向量的空間旋轉到U這組正交基向量空間，並對每個方向做一定的縮放，縮放因子就是Σ中的各個奇異值，同時如果V的維度比U大，那麼這個過程還包含了投影。
可見SVD將一個矩陣原本混合在一起的三種作用效果給分離了開來。

3、特徵值分解則是對旋轉和縮放兩種效應的歸併。因為特徵值分解中的A為方陣，顯然是不存在投影效應的。
特徵值和特徵向量由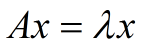得到。即對於一個處於A的特徵向量x方向上的向量v而言，Av對v的線性變換作用則只表現在縮放上。或者說，我們找到了一組基（特徵向量們），在這組基下，矩陣的作用效果僅僅是縮放。
當A為實對稱矩陣時，特徵向量之間是相互正交的，可以將上式寫作，這樣看形式和SVD類似，即矩陣A將一個向量從x這組基的空間旋轉到x這組基的空間上，並在每個方向進行了縮放，由於前後兩組基都是x，即沒有進行旋轉和投影。