機器學習思維導圖

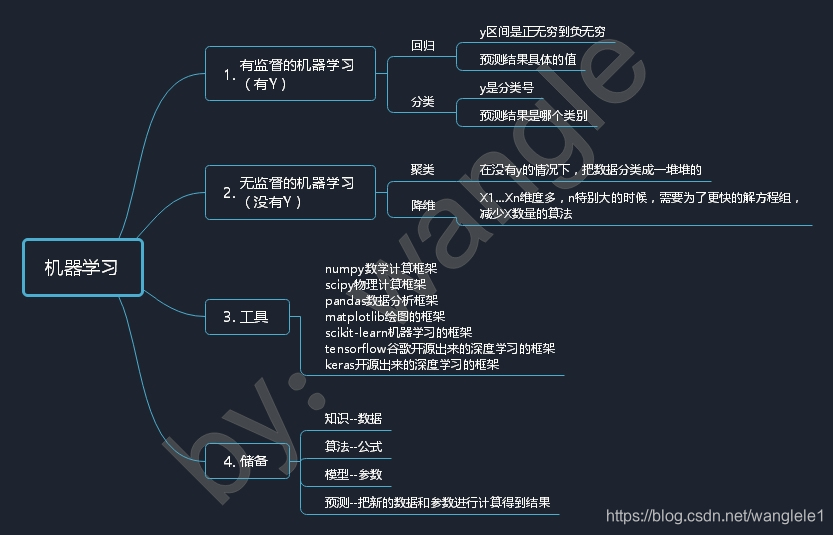
一，什麼是線性迴歸

線性：y=a*x 一次方的變化
迴歸：迴歸到平均值

簡單線性迴歸
演算法==公式
一元一次方程組

一元指的一個X：影響Y的因素，維度
一次指的X的變化：沒有非線性的變化

y = a*x + b
x1,y1 x2,y2 x3,y3 x4,y4 …

做機器學習，沒有完美解
只有最優解~
做機器學習就是要以最快的速度，找到誤差最小的最優解！

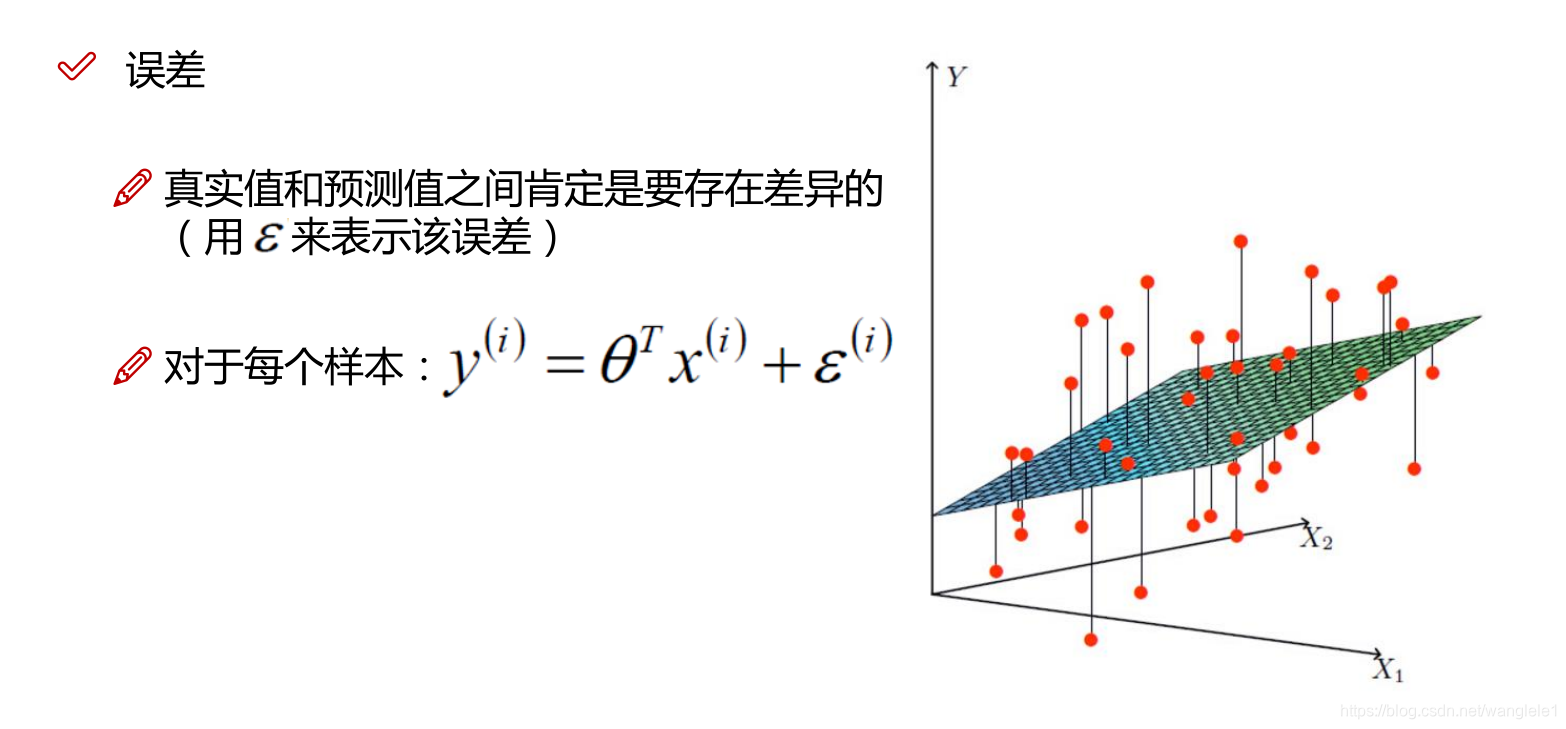
一個樣本的誤差：
yi^ - yi
找到誤差最小的時刻，為了去找到誤差最小的時刻，需要反覆嘗試，a,b
根據最小二乘法去求得誤差
反過來誤差最小時刻的a,b就是最終最優解模型！！！

多元線性迴歸
本質上就是演算法（公式）變換為了多元一次方程組
y = w1x1 + w2x2 + w3x3 + … + wnxn + w0*x0

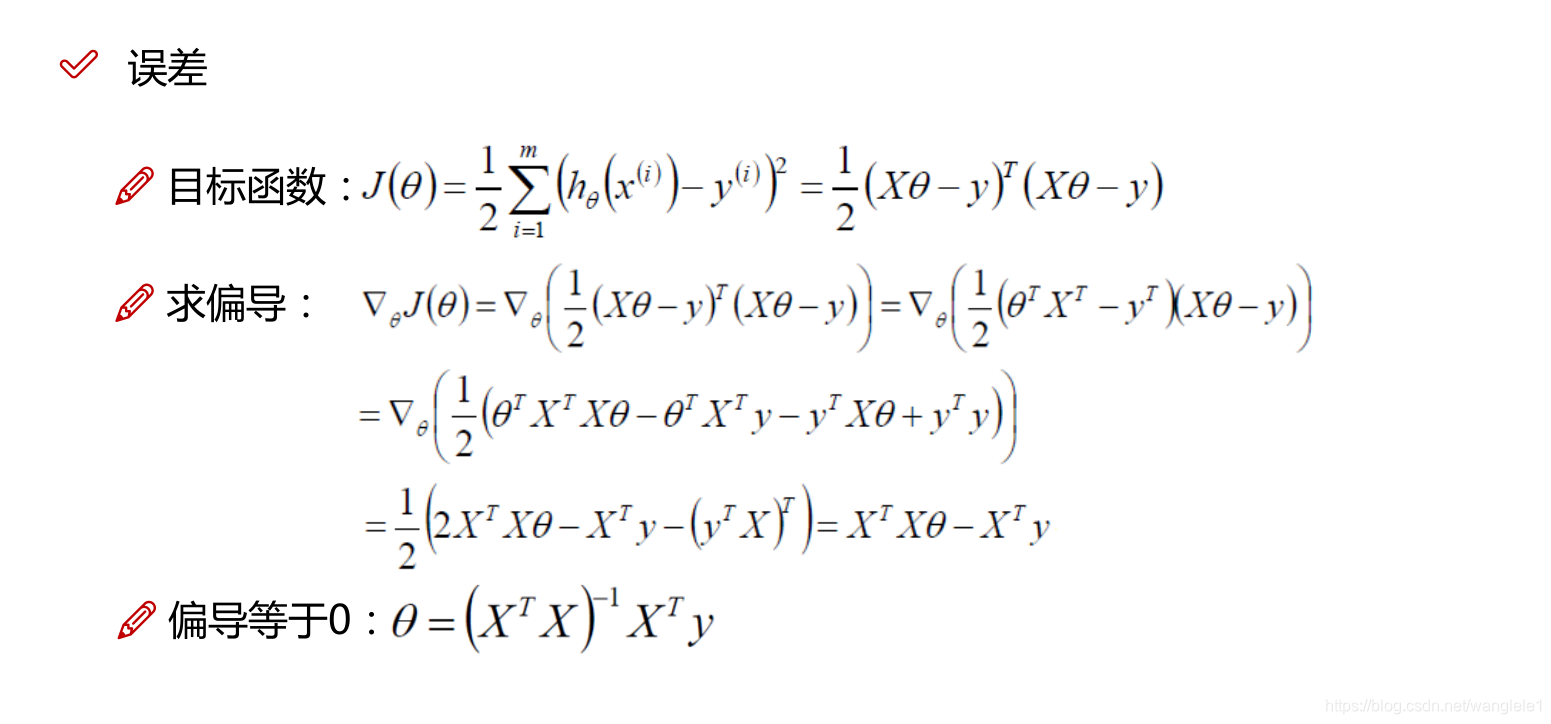
程式碼展示：線性迴歸

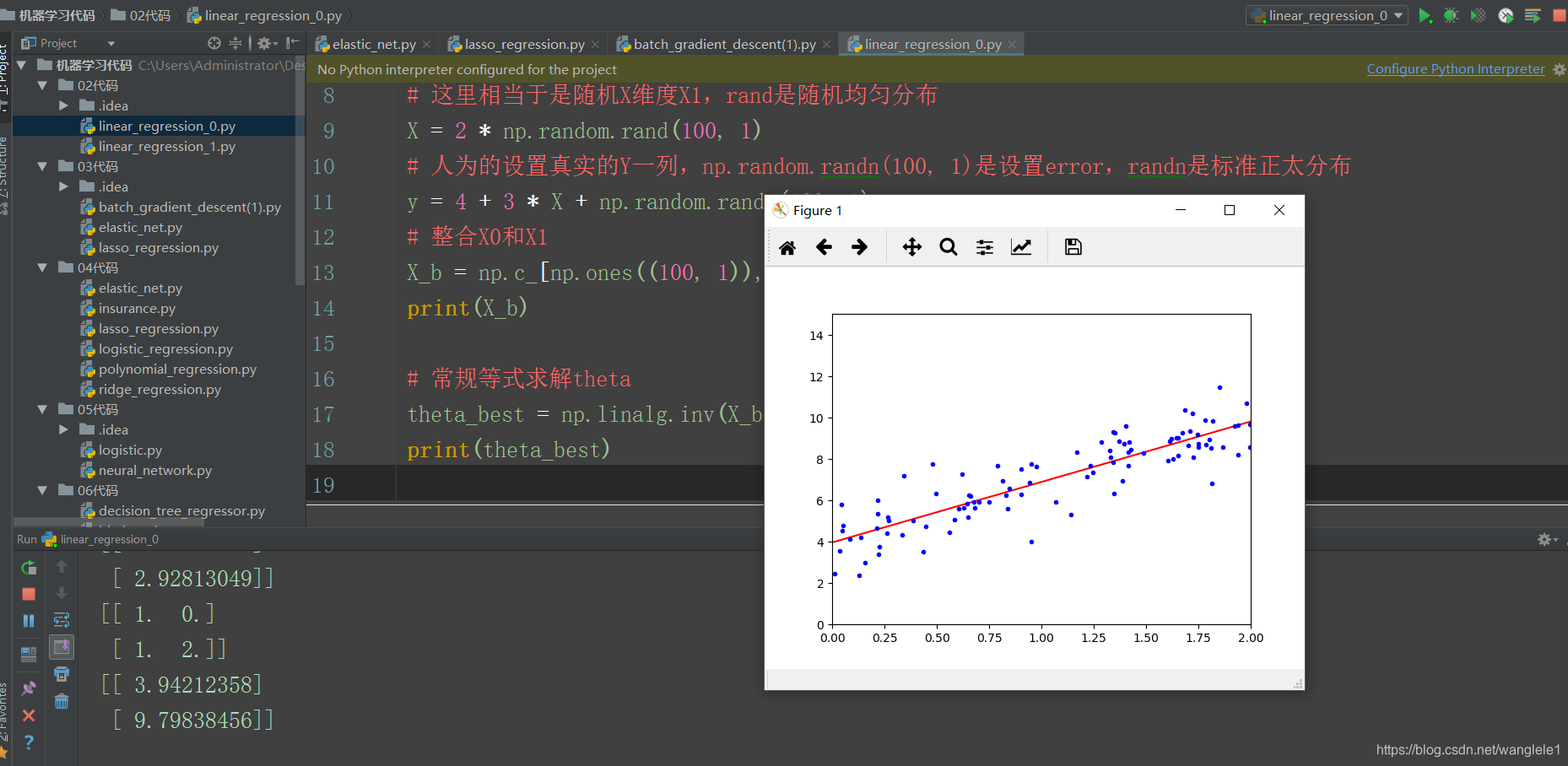
#!/usr/bin/python
# -*- coding: UTF-8 -*-
# 檔名: linear_regression_0.py

import numpy as np
import matplotlib.pyplot as plt

# 這裡相當於是隨機X維度X1，rand是隨機均勻分佈
X = 2 * np.random.rand(100, 1)
# 人為的設定真實的Y一列，np.random.randn(100, 1)是設定error，randn是標準正太分佈
y = 4 + 3 * X + np.random.randn(100, 1)
# 整合X0和X1
X_b = np.c_[np.ones((100, 1)), X]
print(X_b)

# 常規等式求解theta
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print(theta_best)

# 建立測試集裡面的X1
X_new = np.array([[0], [2]]) 
X_new_b = np.c_[(np.ones((2, 1))), X_new]
print(X_new_b)
y_predict = X_new_b.dot(theta_best)
print(y_predict)

plt.plot(X_new, y_predict, 'r-')
plt.plot(X, y, 'b.')
plt.axis([0, 2, 0, 15])
plt.show()
 

執行結果

疑問點

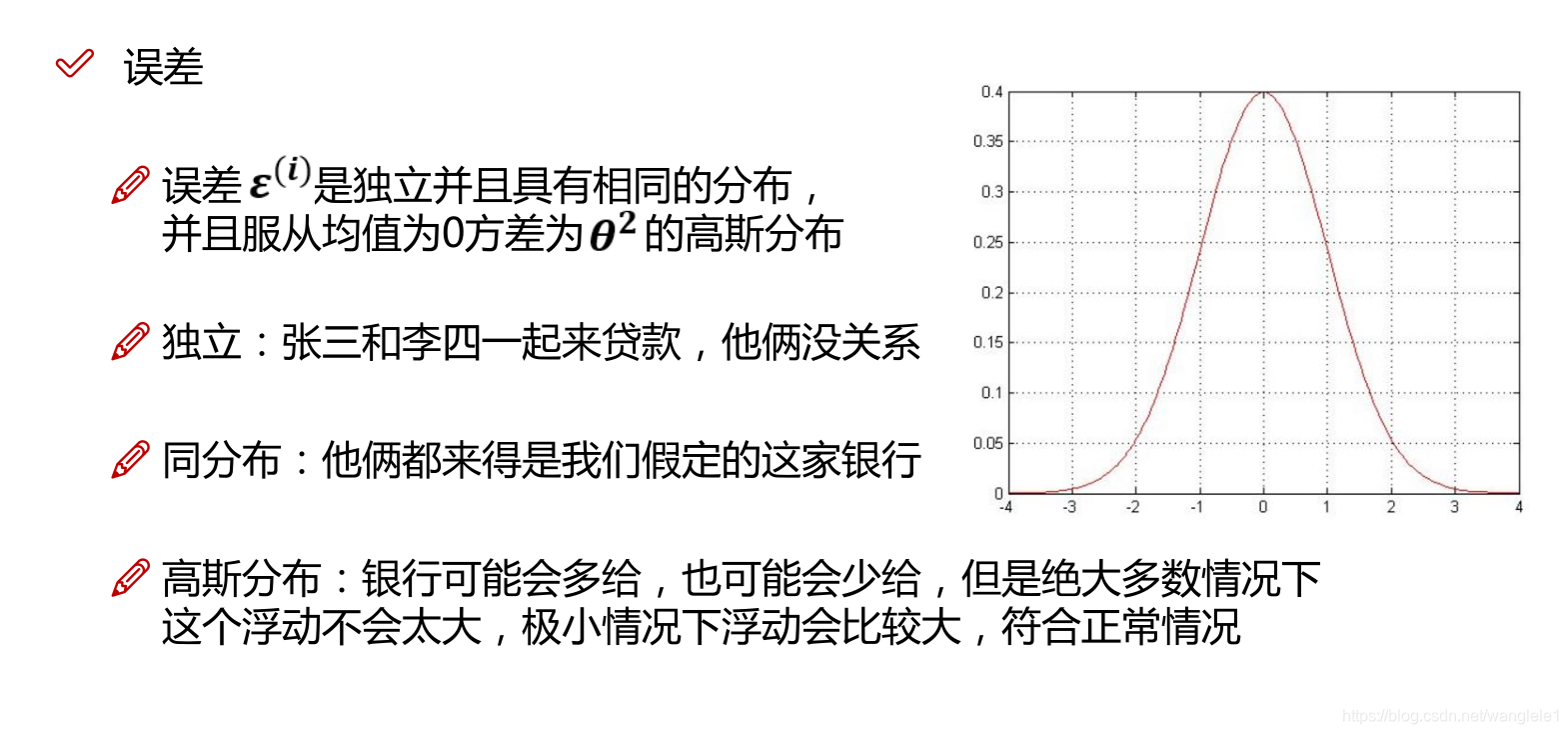
Q：為什麼求總似然的時候，要用正太分佈的概率密度函式？
A：中心極限定理，如果假設樣本之間是獨立事件，誤差變數隨機產生，那麼就服從正太分佈！

Q：總似然不是概率相乘嗎？為什麼用了概率密度函式的f(xi)進行了相乘？
A：因為概率不好求，所以當我們可以找到概率密度相乘最大的時候，就相當於找到了概率相乘最大的時候！

Q：概率為什麼不好求？
A：因為求得是面積，需要積分，麻煩，大家不用去管數學上如何根據概率密度函式去求概率！

Q：那總似然最大和最有解得關係？
A：當我們找到可以使得總似然最大的條件，也就是可以找到我們的DataSet資料集最吻合某個正太分佈！
即找到了最優解！

通過最大似然估計得思想，利用了正太分佈的概率密度函式，推匯出來了損失函式

Q：何為損失函式？
A：一個函式最小，就對應了模型是最優解！預測歷史資料可以最準！

Q：線性迴歸的損失函式是什麼？
A：最小二乘法，MSE，mean squared error，平方均值損失函式，均方誤差

Q：線性迴歸的損失函式有哪些假設？
A：樣本獨立，隨機變數，正太分佈

通過對損失函式求導，來找到最小值，求出theta的最優解！

通過Python呼叫numpy來應用解析解公式之間計算最優解

梯度下降法(重點內容)
1，初始化theta
2，求梯度gradients
3，調整theta
theta_t+1 = theta_t - grad*(learning_rate)
4，回到2迴圈往復第2步和第3步，直到迭代收斂，g約等於0

通過sklearn模組使用LinearRegression
from sklearn.linear_model import LinearRegression
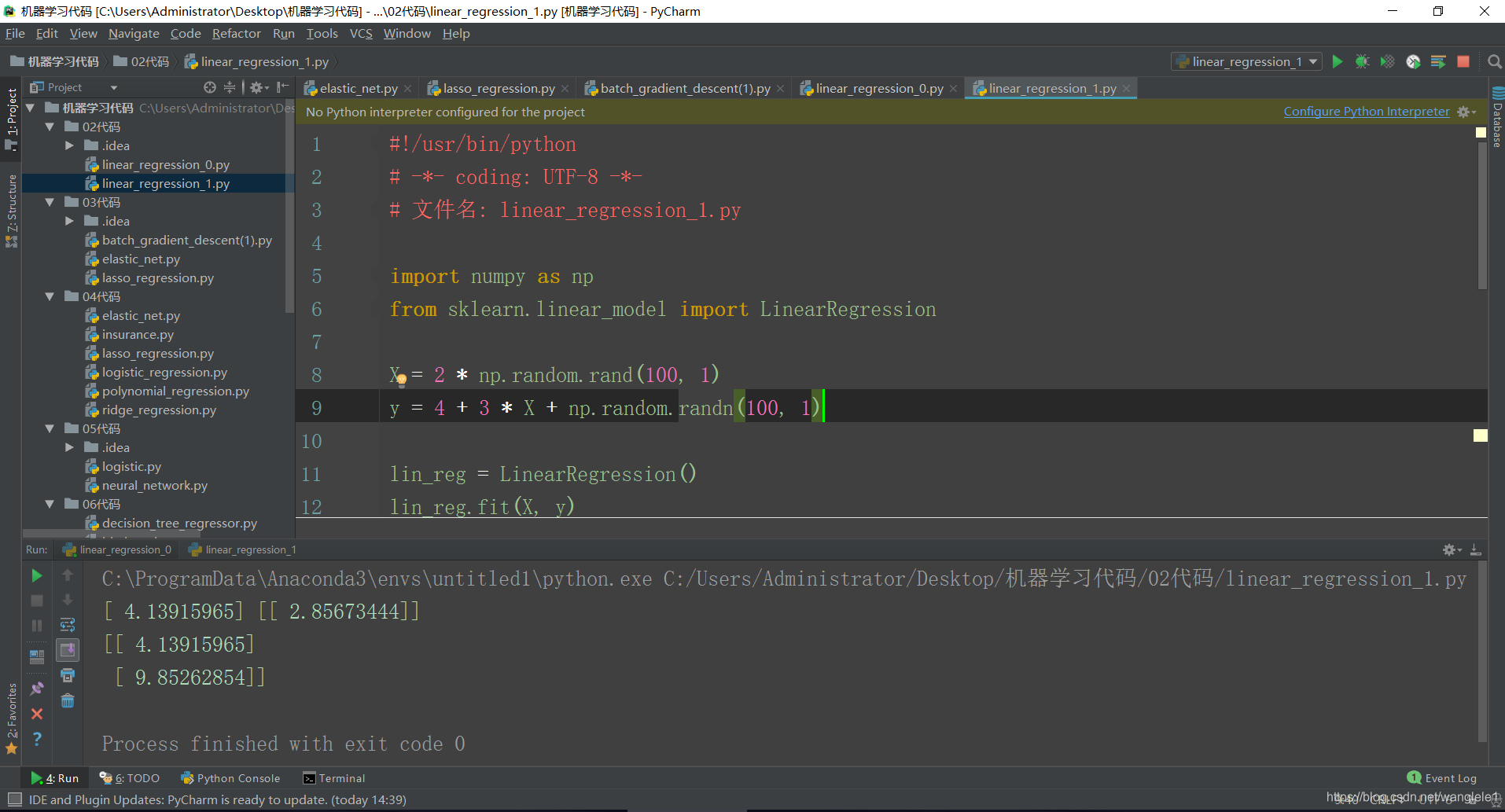
檔名: linear_regression_1.py

程式碼展示：

#!/usr/bin/python
# -*- coding: UTF-8 -*-
# 檔名: linear_regression_1.py

import numpy as np
from sklearn.linear_model import LinearRegression

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

lin_reg = LinearRegression()
lin_reg.fit(X, y)
print(lin_reg.intercept_, lin_reg.coef_)

X_new = np.array([[0], [2]])
print(lin_reg.predict(X_new))

執行結果：