Matlab中可以使用interp函式和griddata函式來實現插值，從而得到擬合曲面

• 從曲面上取樣
• 離散點擬合曲面

1.離散點取樣

為了獲取離散點，首先需要從某個特定的曲面上取樣。
其中利用數學的方法，就是先生成取樣曲線的x-y座標，並根據曲面方程獲取對應的z值；

%我們以螺旋取樣為例
%構建取樣的座標點x-y
theta = 0:0.025*pi:10*pi;
r7 = 0 + 0.1*theta;
x = r7.*cos(theta)+3;
y = r7.*sin(theta)+3;plot(x,y,'.')
[X,Y] = meshgrid(x,y);
%在對應曲面方程上取樣
Z = rand*(sin(X+rand*2*pi)+sin(Y+rand*2*pi));
surf(X,Y,Z);shading interp
figure
z = diag(Z);    %對應x,y座標點處的z
plot3(x,y,z,'.b')
 

原曲面與取樣點雲

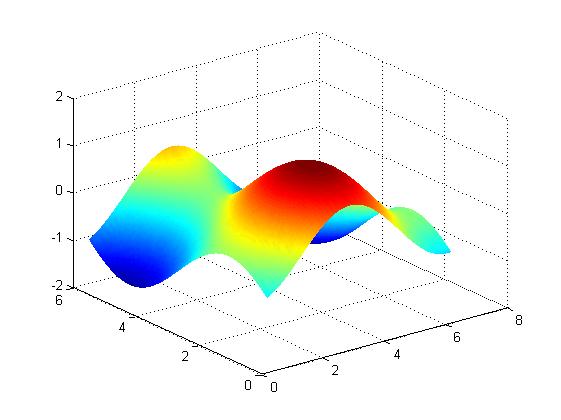
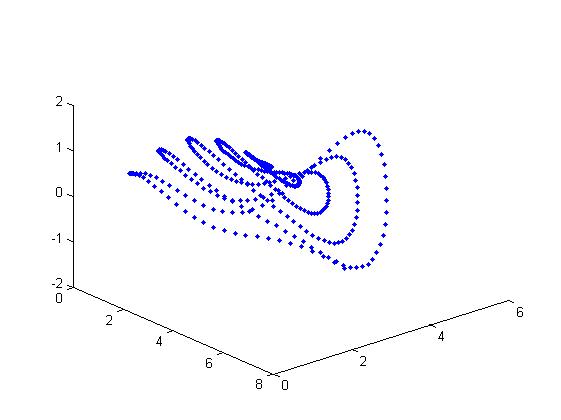
另一種則是利用柵格與插值的方法來獲取對應的z值：

%Based surface
x0 = linspace(0,2*pi,128);
y0 = linspace(0,2*pi,128);
[X0,Y0] = meshgrid(x0,y0);
Z0= rand*(sin(X0+rand*2*pi)+sin(Y0+rand*2*pi));

%而後生成取樣柵格
theta = 0:0.025*pi:10*pi;
r7 = 0 + 0.1*theta;
x = r7.*cos(theta)+3;
y = r7.*sin(theta)+3;plot(x,y,'.')
[X,Y] = meshgrid(x,y);

%此處用重新插值的方法獲得取樣點的座標
%相當與在原圖上做了重新的插值，查到了螺旋線柵格化後的點
Z = interp2(X0,Y0,Z0,X,Y);  
surf(X,Y,Z);shading interp
figure
z = diag(Z);    %對應x,y座標點處的z
plot3(x,y,z,'.b')
 

此時的曲面和採集到的點雲如下：

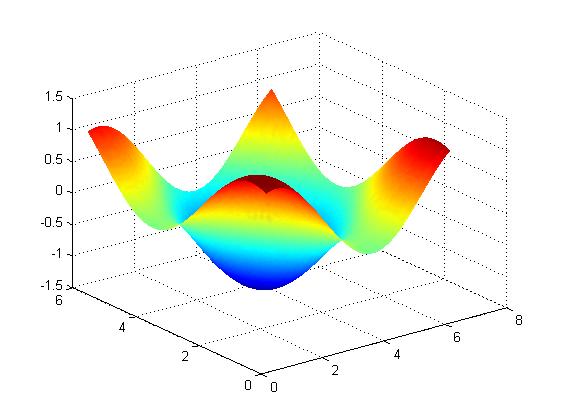
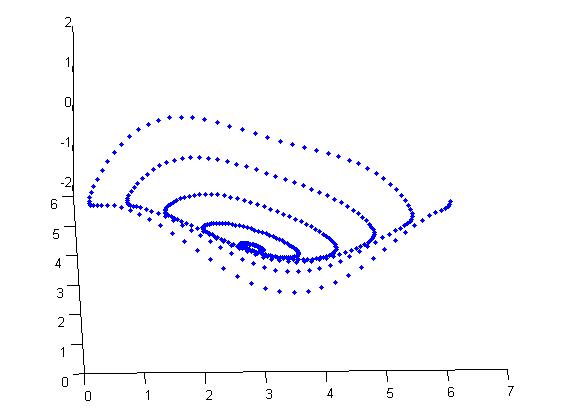
2.曲面擬合

在有了點雲之後，需要將x-y-z資料變成柵格化資料才能夠呼叫mesh,surf等函式繪製圖形。

%目標曲面的大小，需要先生成一個柵格
%一般與點雲大小相當
xn = linspace(0,2*pi,128);
yn = linspace(0,2*pi,128);
[Xn,Yn] = meshgrid(xn,yn);

%利用griddata來插值，從xyz生成柵格資料
%最後一個為插值方法，包linear cubic natural nearest和v4等方法
%v4方法耗時長但較為準確
Zn = griddata(x,y,z,Xn,Yn,'v4'); 

surf(Xn,Yn,Zn);shading interp
figure
mesh(Xn,Yn,Zn)
hold on
plot3(x,y,z,'r+','MarkerSize',3)
 

擬合出的曲面結果，以及包含取樣點的mesh圖：

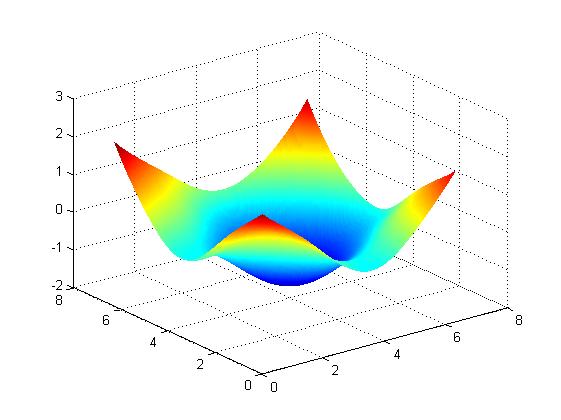
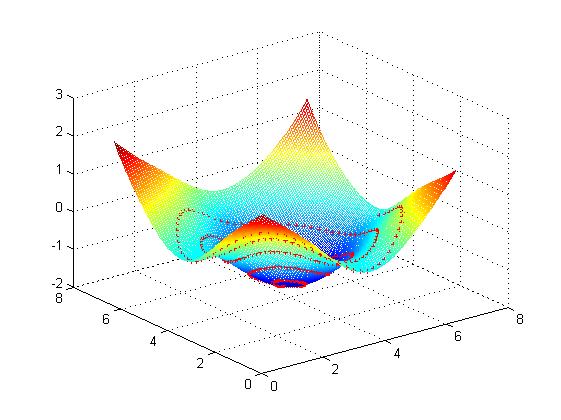
ref:
https://blog.csdn.net/u012302488/article/details/51201238
https://blog.csdn.net/shanchuan2012/article/details/72772191
http://muchong.com/html/201106/3290808.html

pic from pexels.com