利用python學習OpenCV，個人感覺比較方便。函式的形式與C++基本相同，所以切換過來還是比較好的，對於像我這種對python不太熟練的人，使用python的整合開發環境PyCharm進行學習，可以設定斷點除錯，有助於我這類初學者理解掌握。

在我們使用針孔相機時，我們會丟失大量重要的信心，比如說影象的深度，或者說影象上的點和攝像機的距離，因這是一個從3D 到2D 的轉換。因此一個重要的問題就產生了，使用這樣的攝像機我們能否計算除深度資訊呢？答案就是使用多個相機。我們的眼睛就是這樣工作的，使用兩個攝像機（兩個眼睛），這被稱為立體視覺。

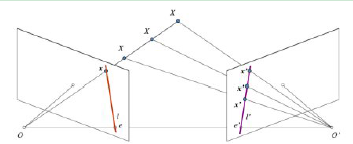
在進入深度影象之前，我們要先掌握一些多視角幾何的基本概念。在本節中我們要處理對極幾何。下圖為使用兩臺攝像機同時對一個一個場景進行拍攝的示意圖。

如果只是用一臺攝像機我們不可能知道3D 空間中的X 點到影象平面的距離，因為OX 連線上的每個點投影到影象平面上的點都是相同的。但是如果我們也考慮上右側影象的話，直線OX 上的點將投影到右側影象上的不同位置。所以根據這兩幅影象，我們就可以使用三角測量計算出3D 空間中的點到攝像機的距離（深度）。這就是整個思路。

直線OX 上的不同點投射到右側影象上形成的線l′ 被稱為與x 點對應的極線。也就是說，我們可以在右側影象中沿著這條極線找到x 點。它可能在這條直線上某個位置（這意味著對兩幅影象間匹配特徵的二維搜尋就轉變成了沿著極線的一維搜尋。這不僅節省了大量的計算，還允許我們排除許多導致虛假匹配的點）。這被稱為對極約束

O 和O' 是攝像機的中心。從上面的示意圖可以看出，右側攝像機的中心O' 投影到左側影象平面的e 點，這個點就被稱為極點。極點就是攝像機中心連線與影象平面的交點。因此點e' 是左側攝像機的極點。有些情況下，我們可能不會在影象中找到極點，它們可能落在了影象之外（這說明這兩個攝像機不能拍攝到彼此）。

所有的極線都要經過極點。所以為了找到極點的位置，我們可以先找到多條極線，這些極線的交點就是極點。本節我們的重點就是找到極線和極點。為了找到它們，我們還需要兩個元素，本徵矩陣（E）和基礎矩陣（F）。本徵矩陣包含了物理空間中兩個攝像機相關的旋轉和平移資訊。如下圖所示。

基礎矩陣F 除了包含E 的資訊外還包含了兩個攝像機的內參數。由於F包含了這些內參數，因此它可以它在畫素座標系將兩臺攝像機關聯起來（如果使用是校正之後的影象並通過除以焦距進行了歸一化，F=E）。簡單來說，基礎矩陣F 將一副影象中的點對映到另一幅影象中的線（極線）上。這是通過匹配兩幅影象上的點來實現的。要計算基礎矩陣至少需要8 個點（使用8 點演算法）。點越多越好，可以使用RANSAC 演算法得到更加穩定的結果。

下面是相關的測試程式碼：

# -*- coding:utf-8 -*-
__author__ = 'Microcosm'

import cv2
import numpy as np
from matplotlib import pyplot as plt

img_L = cv2.imread("E:\python\Python Project\opencv_showimage\images\stereoBM\\tsukuba_l.png",0)
img_R = cv2.imread("E:\python\Python Project\opencv_showimage\images\stereoBM\\tsukuba_r.png",0)

sift = cv2.SIFT()

kp1,des1 = sift.detectAndCompute(img_L,None)
kp2,des2 = sift.detectAndCompute(img_R,None)

FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks=50)

# 利用FLANN匹配器
flann = cv2.FlannBasedMatcher(index_params, search_params)
matches = flann.knnMatch(des1,des2,k=2)

good = []
pts1 = []
pts2 = []

# 尋找匹配點對
for i,(m,n) in enumerate(matches):
    if m.distance < 0.2*n.distance:
        good.append(m)
        pts1.append(kp1[m.queryIdx].pt)
        pts2.append(kp2[m.trainIdx].pt)

pts1 = np.float32(pts1)
pts2 = np.float32(pts2)
# 根據匹配點對計算基礎矩陣
F, mask = cv2.findFundamentalMat(pts1,pts2,cv2.FM_LMEDS)

# 尋則內部點
pts1 = pts1[mask.ravel()==1]
pts2 = pts2[mask.ravel()==1]

# 繪製極線的函式
def drawlines(img1,img2,lines,pts1,pts2):
    r,c = img1.shape
    img1 = cv2.cvtColor(img1,cv2.COLOR_GRAY2BGR)
    img2 = cv2.cvtColor(img2,cv2.COLOR_GRAY2BGR)
    for r,pt1,pt2 in zip(lines,pts1,pts2):
        color = tuple(np.random.randint(0,255,3).tolist())
        x0,y0 = map(int,[0,-r[2]/r[1]])   # 對映成整數值
        x1,y1 = map(int,[c,-(r[2]+r[1]*c)/r[1]])
        cv2.line(img1, (x0,y0),(x1,y1),color,1)
        cv2.circle(img1,tuple(pt1),5,color,-1)
        cv2.circle(img2,tuple(pt2),5,color,-1)
    return img1,img2

# 計算並繪製兩幅影象中的極線
lines1 = cv2.computeCorrespondEpilines(pts2.reshape(-1,1,2),2,F)
lines1 = lines1.reshape(-1,3)
img5,img6 = drawlines(img_L,img_R,lines1,pts1,pts2)

lines2 = cv2.computeCorrespondEpilines(pts1.reshape(-1,1,2),2,F)
lines2 = lines2.reshape(-1,3)
img3,img4 = drawlines(img_R,img_L,lines2,pts2,pts1)

plt.subplot(121),plt.imshow(img5),plt.title('leftImage'),plt.xticks([]),plt.yticks([])
plt.subplot(122),plt.imshow(img3),plt.title('rightImage'),plt.xticks([]),plt.yticks([])
plt.show()