鬆弛操作

Dijkstra演算法和BellmanFord演算法都是基於這個簡單的操作。
下面我們來了解這個簡單而重要的操作：

1. 線鬆弛
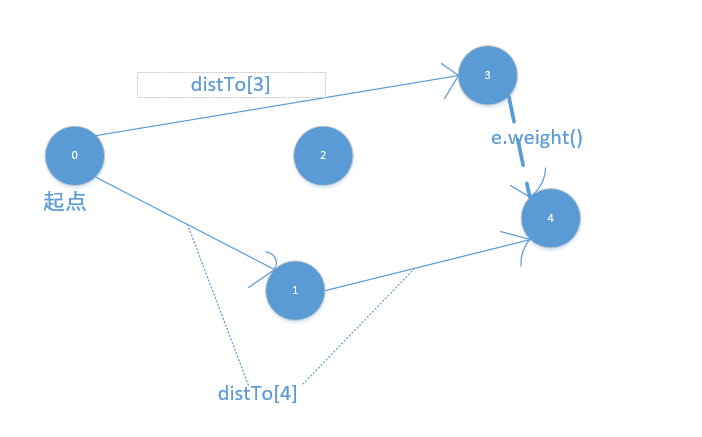
   線鬆弛也就是處理
   起點到邊的兩個頂點距離與兩個頂點直接距離的問題。
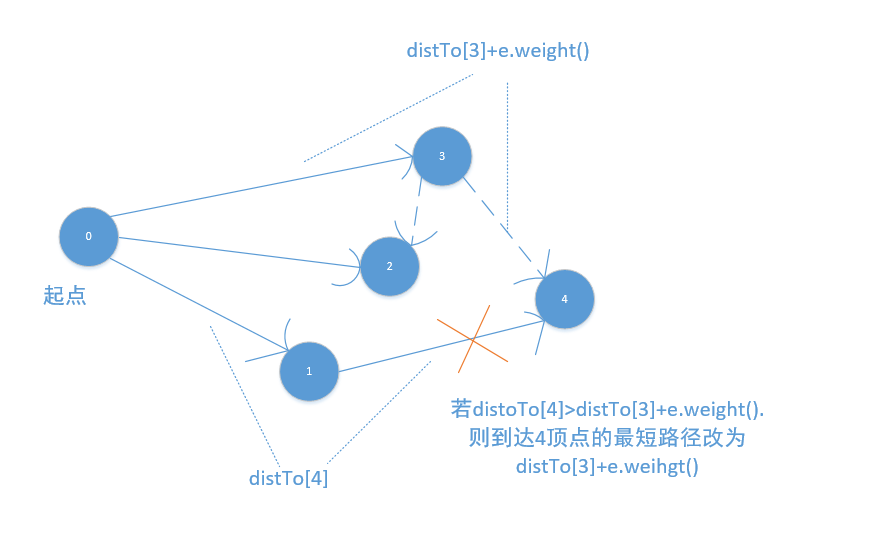
   如：假如distTo[4]>distTo[3]+e.weight()，則會修改到達4頂點的最短路徑，否則不變。
   

2.點鬆弛
點鬆弛其實就是對頂點的每一條發出的邊都進行一次線鬆弛操作。
如圖：邊3->2，同樣要進行線鬆弛。

Dijkstra演算法

直接附上程式碼了（有詳細解釋）
效能：任何情況下都能保證較好的效能（當然，此演算法不能存在負值的邊）

package
 
 ShortestPath;

import java.util.Stack;

/**
  *基於解決加非負權值有向圖的單起點的最短路徑問題Dijkstra演算法
  *該類維護了三個變數：{@link DirectedEdge}類陣列{@link path}；{@link double}陣列{@link distTo};{@link IndexMinPQ}優先佇列{@link pq}
  *<p>其中path儲存了到達某個頂點的最短路徑；distTo[w]：起點到w的權值和（初始都為0，起點除外）；pq：儲存了頂點的優先佇列
  *<p>演算法思想：每次都為最短路徑增加一條邊，直至涵蓋所有的頂點或者非樹頂點的distTo都為無窮大的時候結束。
  * @author
 
  羅正 
  * @date 2016年9月23日 上午9:41:42 
**/
public class DijkstraSP {

    private IndexMinPQ<Double> pq;  //頂點的優先佇列
    private double[] distTo;    //每個頂點的距離（初始化為無窮大）
    private DirectedEdge[] path;    //儲存了關鍵路徑的邊

    /**
     * 構造的Dijkstra函式，傳入帶權值無向圖g，以及起點s
     * */
    public DijkstraSP(EdgeDigraph g,int
 
 s)
    {
        //初始化
        distTo = new double[g.V()];
        pq = new IndexMinPQ<Double>(g.V());
        path = new DirectedEdge[g.V()];

        //將所有頂點與起點的距離都初始化為無窮大
        for(int v = 0;v<g.V();v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        //將起點距離設定為0，並加入到優先佇列中
        distTo[s] = 0.0;
        pq.insert(s, 0.0);
        while(!pq.isEmpty())
        {
            relax(g,pq.delMin());
        }

    }

    /**
     * 最短路徑的關鍵方法：邊的鬆弛（relaxation）
     * <p>該方法會維護所有v到達的邊（即以v為起點的邊），假設存在v->w(非樹)：
     * 首先方法會迴圈到v->w這條邊;
     * <p>假若：起點到w的距離（distTo[w]）比起點到達v的距離（distTo[v]）和v->w的邊（(v->w).weight()）還要大的話；
     * <p>那麼是不是對於求最短路徑來說，到達w頂點的路徑是不是就要變成先到達v再由v到達w呢，這是顯然的。
     * @param g
     * @param v
     */
    private void relax(EdgeDigraph g,int v)
    {
        for(DirectedEdge e : g.adj(v))
        {
            int w = e.to();
            if(distTo[w]>distTo[v]+e.weight())
            {
                distTo[w] = distTo[v]+e.weight();
                path[w] = e;
                /*假如w已經包含在最短路徑中，也還是要修改到達w的路徑的，因為已經更短了啊*/
                if(pq.contains(w))
                    pq.change(w, distTo[w]);
                else
                    pq.insert(w, distTo[w]);
            }
        }
    }

    public double distto(int v)
    {
        return distTo[v];
    }

    public boolean hasPath(int v)
    {
        return distTo[v]<Double.POSITIVE_INFINITY;
    }

    public Iterable<DirectedEdge> path(int v)
    {
        if(!hasPath(v))
            return null;
        else
        {
            Stack<DirectedEdge> pathTo = new Stack<>();
            for(DirectedEdge e = path[v];e != null; e = path[e.from()])
                pathTo.push(e);
            return pathTo;
        }
    }

    public static void main(String[] args) {
        DirectedEdge e1 = new DirectedEdge(0, 1, 100);
        DirectedEdge e2 = new DirectedEdge(1, 3, 200);
        DirectedEdge e3 = new DirectedEdge(0, 2, 200);
        DirectedEdge e4 = new DirectedEdge(2, 3, 200);
        EdgeDigraph g = new EdgeDigraph(4);
        g.addEdge(e1);
        g.addEdge(e2);
        g.addEdge(e3);
        g.addEdge(e4);

        DijkstraSP dij = new DijkstraSP(g, 0);
        System.out.println(dij.path(3));
    }

}

Bellman—Ford 演算法

這裡討論的是基於佇列的BellmanFord演算法的實現。

此演算法適用於任何情況（當然，存在負權值環對於求最短路徑是沒有意義的。）

package ShortestPath;

import java.util.ArrayDeque;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

import minSpanningTree.Edge;

/**
  *基於佇列的Bellman-Ford演算法: 將起點的distTo[s]初始為0，將其他所有頂點distTo初始為無窮大，任意順序放鬆所有邊，重複V輪。
  *<p>思路：與Dijkstra演算法類似，double陣列distTo意義一樣；
  *佇列queue儲存放鬆的頂點；不同的是增加一個標記標記重複每輪放鬆的頂點和下一輪放鬆的頂點（使得佇列不會重複儲存頂點），下輪在放鬆函式裡設定為true，以便保證下輪不重複；
  *Bellman—Ford演算法對於一般加權值圖，其中就包括了負值權值（但是假若存在負權值的環，則對於求最短路徑則沒有意義了）
  *<p>1>首先明白為什麼存在負權值換對於求最短路徑沒有意義？因為在環裡每重複一次，我們都能得到一條更短的路徑。
  *<p>2>加入存在負權值環，relax過程會有什麼異常呢？由上一個問題答案，我們知道，這個過程假如和Dijstra演算法無異，則會無限迴圈下去
  *<p>3>如何確定存在負權值環呢？我們前面已經知道，重複V輪，我們就能得到最短路徑，
  *事實上我們只需要V-1輪結束後，就能得到最短路徑，所以，假如重複了V輪，是不是就說明存在負權值環了呢
  *
  * @author  羅正 
  * @date 2016年9月23日 下午3:40:23 
**/
public class BellmanFordSP {

    private double[] distTo;
    private boolean[] onQ;
    private DirectedEdge[] edgeTo;
    private Queue<Integer> queue;

    //對於檢測負權值環定義的變數
    private int count;
    private Iterable<DirectedEdge> cycle;

    /**
     * 此函式和Dijkstra演算法的函式並無太大區別，只是增加了onQ[]，標記頂點。
     * @param g
     * @param s
     */
    public BellmanFordSP(EdgeDigraph g,int s)
    {
        distTo = new double[g.V()];
        onQ = new boolean[g.V()];
        int count = 0;
        queue = new ArrayDeque<>();
        edgeTo = new DirectedEdge[g.V()];

        for(int i = 0;i<g.V();i++)
            distTo[i] = Double.POSITIVE_INFINITY;

        distTo[s] = 0.0;
        onQ[s] = true;
        queue.add(s);
        while(!queue.isEmpty())
        {
            int v = queue.remove();
            onQ[v] = false;
            relax(g,v);
        }
    }

    /*放鬆操作*/
    private void relax(EdgeDigraph g,int v)
    {
        for(DirectedEdge e : g.adj(v))
        {
            int w = e.to();
            if(distTo[w] > distTo[v]+e.weight())
            {
                distTo[w] = distTo[v]+e.weight();
                edgeTo[w] = e;
                if(!onQ[w])
                {
                    queue.add(w);
                    onQ[w] = true;
                }
            }

            //假如存在環，則count == V
            if(count++ % g.V() == 0)
                findNegativeCycle();
        }
    }

    public double distto(int v)
    {
        return distTo[v];
    }

    public boolean hasPath(int v)
    {
        return distTo[v]<Double.POSITIVE_INFINITY;
    }

    public Iterable<DirectedEdge> path(int v)
    {
        if(!hasPath(v))
            return null;
        else
        {
            Stack<DirectedEdge> pathTo = new Stack<>();
            for(DirectedEdge e = edgeTo[v];e != null; e = edgeTo[e.from()])
                pathTo.push(e);
            return pathTo;
        }
    }

    //檢測環函式，並儲存環
    private void findNegativeCycle()
    {
        int V = edgeTo.length;
        EdgeDigraph g;
        g = new EdgeDigraph(V);

        for(int v = 0;v<V;v++)
        {
            if(edgeTo[v] != null)
                g.addEdge(edgeTo[v]);
        }

        EdgeWeightedDirectedCycle c = new EdgeWeightedDirectedCycle(g);
        cycle = c.cycle();
    }

    public boolean hasNegativeCycle()
    {
        return cycle == null;
    }

    public Iterable<DirectedEdge> negativeCycle()
    {
        return cycle;
    }
}