最大似然估計 MLE

給定一堆資料，假如我們知道它是從某一種分佈中隨機取出來的，可是我們並不知道這個分佈具體的參，即“模型已定，引數未知”。

例如，對於線性迴歸，我們假定樣本是服從正態分佈，但是不知道均值和方差；或者對於邏輯迴歸，我們假定樣本是服從二項分佈，但是不知道均值，邏輯迴歸公式得到的是因變數y的概率P = g(x), x為自變數，通過邏輯函式得到一個概率值，y對應離散值為0或者1，Y服從二項分佈，誤差項服從二項分佈，而非高斯分佈，所以不能用最小二乘進行模型引數估計，可以用極大似然估計來進行引數估計； 因此最大似然估計（MLE，Maximum Likelihood Estimation）就可以用來估計模型的引數。MLE的目標是找出一組引數，使得模型產生出觀測資料的概率最大：

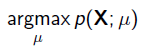
其中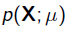就是似然函式，表示在引數下出現觀測資料的概率。我們假設每個觀測資料是獨立的，那麼有

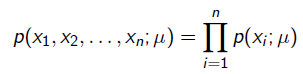
為了求導方便，一般對目標取log。 所以最優化對似然函式等同於最優化對數似然函式：

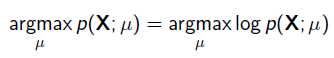
舉一個拋硬幣的簡單例子。 現在有一個正反面不是很勻稱的硬幣，如果正面朝上記為H，方面朝上記為T，拋10次的結果如下：

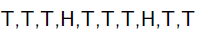
求這個硬幣正面朝上的概率有多大？

很顯然這個概率是0.2。現在我們用MLE的思想去求解它。我們知道每次拋硬幣都是一次二項分佈，設正面朝上的概率是，那麼似然函式為：

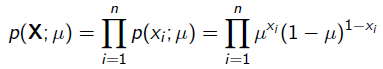
x=1表示正面朝上，x=0表示方面朝上。那麼有：

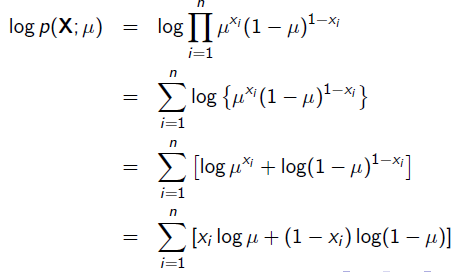
求導：

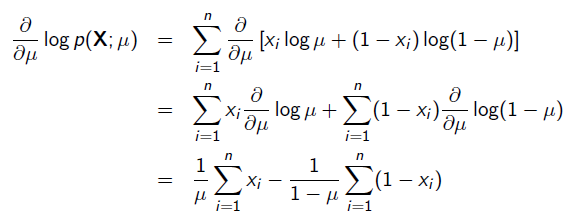
令導數為0，很容易得到：

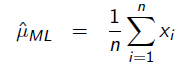
也就是0.2 。

 最大後驗概率  MAP

以上MLE求的是找出一組能夠使似然函式最大的引數，即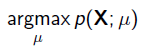。 現在問題稍微複雜一點點，假如這個引數有一個先驗概率呢？比如說，在上面拋硬幣的例子，假如我們的經驗告訴我們，硬幣一般都是勻稱的，也就是=0.5的可能性最大，=0.2的可能性比較小，那麼引數該怎麼估計呢？這就是MAP要考慮的問題。 MAP優化的是一個後驗概率，即給定了觀測值後使概率最大：

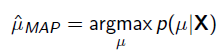
把上式根據貝葉斯公式展開：

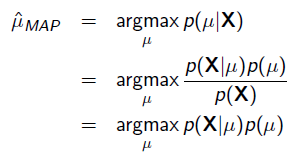
我們可以看出第一項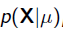就是似然函式，第二項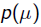就是引數的先驗知識。取log之後就是：

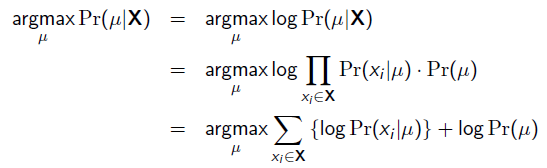
回到剛才的拋硬幣例子，假設引數有一個先驗估計，它服從Beta分佈，即：

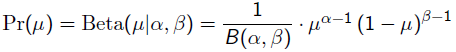
而每次拋硬幣任然服從二項分佈：

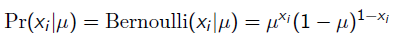
那麼，目標函式的導數為：

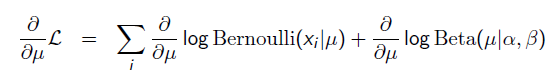
求導的第一項已經在上面MLE中給出了，第二項為：

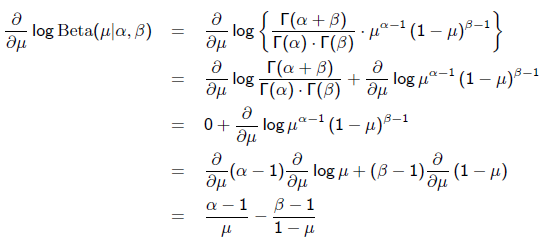
令導數為0，求解為：

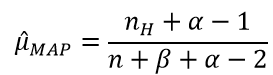
其中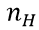，表示正面朝上的次數。這裡看以看出，MLE與MAP的不同之處在於，MAP的結果多了一些先驗分佈的引數。

補充知識： Beta分佈

Beat分佈是一種常見的先驗分佈，它形狀由兩個引數控制，定義域為[0,1]

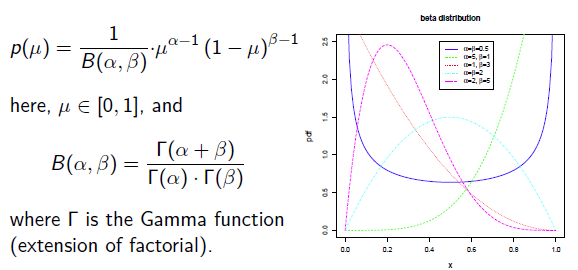
Beta分佈的最大值是x等於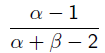的時候：

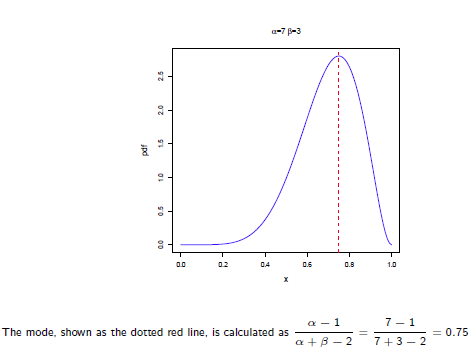
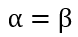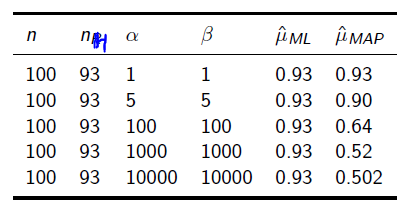
所以在拋硬幣中，如果先驗知識是說硬幣是勻稱的，那麼就讓。 但是很顯然即使它們相等，它兩的值也對最終結果很有影響。它兩的值越大，表示偏離勻稱的可能性越小：