一.熟悉MPI並行程式設計環境

1.硬體
電腦:HP暗夜精靈
記憶體:4G
處理器:ntel® Core™ i5-6300HQ CPU @ 2.30GHz × 4
顯示卡:NVIDIA 960M

2.軟體
系統:Ubuntu 16.04LTS
MPI版本:MPICH2

二.計算π$\pi$

1.問題描述
已知π$\pi$計算公式：π=∫1041+x2dx$\pi ={\int }_0^1\frac{4}{1+x^2}dx$　已知有如下兩種演算法求其數值積分:

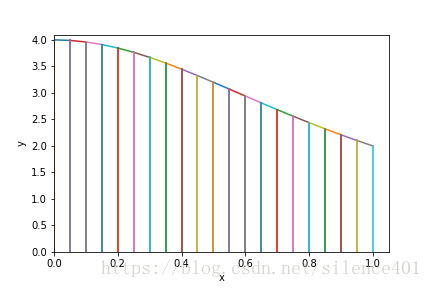
• 1.用梯形面積進行數值計算
  　　　　　　　　
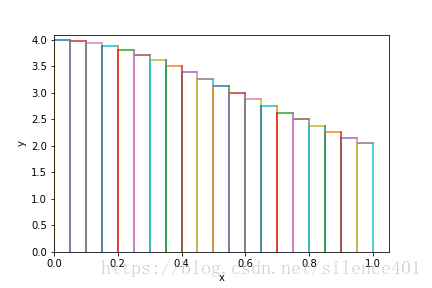
• 2.用矩形面積進行數值計算
  　　　　　　　　
  2.程式概要設計(用梯形法計算)

MPI_Bcast(&n,1,MPI_INT,0
 
,MPI_COMM_WORLD);//把n廣播給所有程序
        MPI_Barrier(MPI_COMM_WORLD);
        init_size=1.0/n;//把圖形分為n個梯形，每個梯形的高為１/n
        for(int i=rank+1;i<=n;i+=proc_num)//每個程序計算n/proc_num個梯形
        {
            x1=init_size*(i);
            x2=init_size*(i-1);
            x1=4/(1+x1*x1);
            x2=4/(1+x2*x2);
            part_sum=part_sum+x1+x2;//把梯形的上底和下底計算到部分和中
 

        }
        temp_pi=init_size*part_sum/2;//計算該程序所計算的梯形面積和
  //歸約函式，對所有程序所計算的面積求和即是pi值 
       MPI_Reduce(&temp_pi,&cal_pi,1,MPI::DOUBLE,MPI::SUM,0,MPI_COMM_WORLD);

3.實驗結果及其分析

部分結果截圖如下:
　　　　　
　　　　　
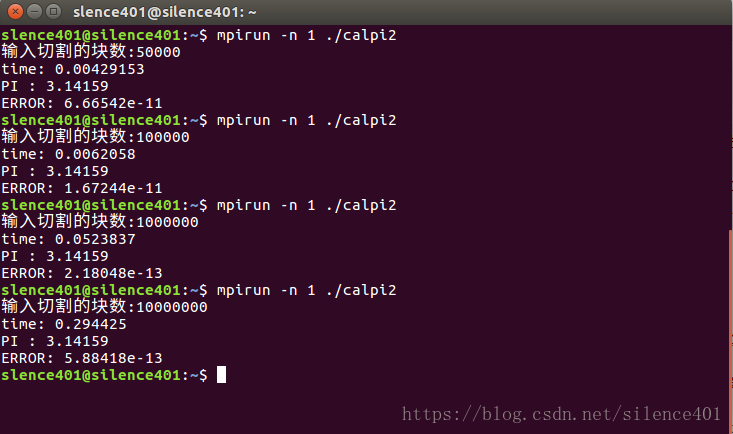
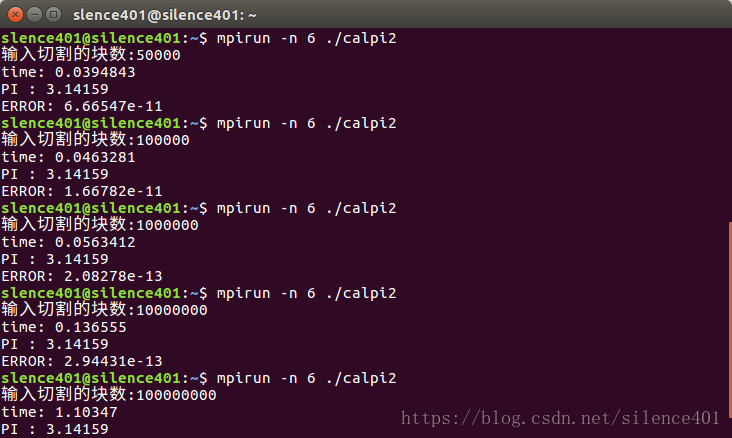
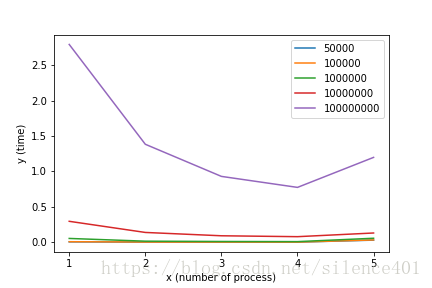
結果分析:　
　　　　　　　　　

　　從上圖可知，在我的計算機上當開四個程序時效能達到最大，因為我的計算機是四核的可以做到四個程序真正的並行 .當資料兩較小時，無並行的比並行的更快的主要原因是計算量小的時候MPI通訊的時間佔了程序時間開銷的大部分.

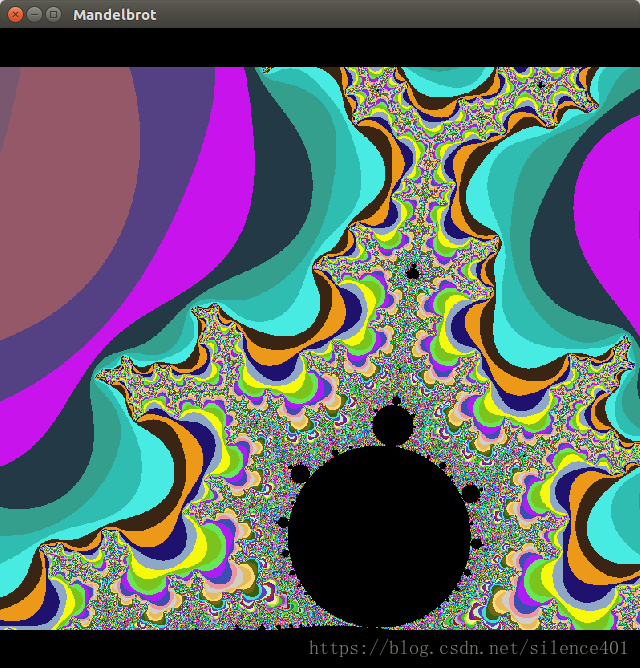
三.Mandelbrot集

1.問題描述
曼德勃羅特集是人類有史以來做出的最奇異,最瑰麗的幾何圖形,曾被稱為”上帝的指紋”. 這個點集均出自公式zn+1=z2n+c$z_{n+1}=z_n^2+c$,所有使得無限迭代後的結果能保持有限數值的複數c的集合構成曼德勃羅特集.假定迭代一定次數後的複數即為曼德勃羅特數,計算一定區間的曼德勃羅特集,並根據數字不同的迭代次數給該點設為不同的顏色.滑動滑鼠,即可計算一定區域的曼德勃羅特集並顯示出來
2.程式概要設計
　　　　　　　　　　　
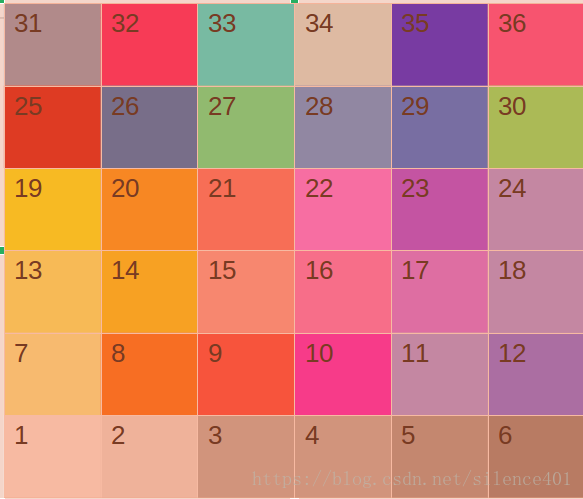
　　　　　　　　　　　把區域分為n∗n$n\ast n$的區域按順序依次分給空閒的程序

//定義Zn+1=Zn^2+c的運算
  ComplexNumber f(ComplexNumber z, ComplexNumber c) 
    {   
        ComplexNumber result;   
        result.real=c.real+z.real*z.real-z.imag*z.imag;   
        result.imag=c.imag+z.imag*z.real+z.real*z.imag;   
        return result;  
    }   

//定義曼德勃羅特的計算步驟,並在recv陣列中記錄該點迭代的次數
 void Mandelbrot(double Xmin,double dx, int xloop, int xfrom, double Ymin,  double dy, int yloop, int yfrom)   
    {   
        int x, y, k;   
        ComplexNumber c, z;   
        for (x=0; x<xloop; x++)   
        {   
            c.real = Xmin+x*dx;   
            for (y=0; y<yloop; y++)   
            {   
                c.imag = Ymin+y*dy;   
                z.real = z.imag = 0.0f;   
                k = 0;   
                while (k<MAX_ITERATE_DEPTH && (z.real*z.real+z.imag*z.imag)<=MAX_MAGNITUDE)   
                {   
                    z = f(z, c);   
                    k++;   
                }   
                recv[xfrom+x][yfrom+y] = k;   
            }   
        }   
    }   

                // 對於一個程序如果接收到了再計算的命令,就計算分配給他的區域的曼德勃羅特集,區域資訊存在info結構體中
                if (Redo == status.MPI_TAG)   
                    {   
                        MPI_Recv(&info,1,AreaType,0,Redo,MPI_COMM_WORLD,&status);   
                        int txfrom=(info.xloop%slave_num)*info.sub_xloop;
                        double tymin=(info.xloop/slave_num)*info.Yarea/slave_num+info.Ymin;
                        int tyfrom=(info.xloop/slave_num)*info.sub_yloop; 
                        Mandelbrot(txmin,info.dx,info.sub_xloop,txfrom,tymin,info.dy,info.sub_yloop,tyfrom);
                        MPI_Send(&info.xloop,1,MPI_INT,0,Over,MPI_COMM_WORLD);
                        MPI_Send(recv,PIXEL_NUM,MPI_SHORT,0,Over,MPI_COMM_WORLD);   
                        printf("send from slave %d\n", rank-1);   
                    }   

   //opengl的閒時回撥函式,主程序一直再執行該函式,接受子程序的資料,當接受到一個程序發來的資料時,
   主程序判斷還有無未計算的區域,如果有就分配給該程序
    void Idle()    
    {   
        //printf("34");
        static int recved = 0;   
        int pos;
        int i, j, x, y;   
        int xfrom, yfrom;   
        int flag, slave_rank;   
        MPI_Status status;   
        MPI_Iprobe(MPI_ANY_SOURCE,Over,MPI_COMM_WORLD, &flag, &status);   
        if (!flag)  return;   
        MPI_Recv(&pos,1,MPI_INT,status.MPI_SOURCE,Over,MPI_COMM_WORLD,&status);
        MPI_Recv(recv,PIXEL_NUM,MPI_SHORT,status.MPI_SOURCE,Over,MPI_COMM_WORLD,&status);   

        if (slave_num*slave_num== ++recved)   
        {   
            recved = 0;   
            end_time = MPI_Wtime();    
            printf("wall clock time = %f\n", end_time-start_time);   
        }   
        slave_rank = status.MPI_SOURCE-1;   
        printf("recieve from slave %d\n", slave_rank);   
        i = slave_rank;   
        xfrom = (pos%slave_num)*info.sub_xloop;   
        yfrom = (pos/slave_num)*info.sub_yloop;       
        for(x=0; x<info.sub_xloop; x++)   
        {   
                for (y=0; y<info.sub_yloop; y++)   
                    indices[xfrom+x][yfrom+y] = recv[xfrom+x][yfrom+y];   
        }
        if(count<slave_num*slave_num)
       {
        MPI_Send(&part[count],1,AreaType,slave_rank+1,Redo,MPI_COMM_WORLD);   
        count++;
        }
        glutPostRedisplay();
    }  

　　3實驗.結果及其分析