PCA主成分分析(入門計算+深入解析)(一)
PCA主成分分析(入門+深入)+最大方差理論+幾何意義
Principal components analysis
我們在作資料分析處理時,資料往往包含多個變數,而較多的變數會帶來分析問題的複雜性。主成分分析(Principal components analysis,以下簡稱PCA)是一種通過降維技術把多個變數化為少數幾個主成分的統計方法,是最重要的降維方法之一。它可以對高維資料進行降維減少預測變數的個數,同時經過降維除去噪聲,其最直接的應用就是壓縮資料,具體的應用有:訊號處理中降噪,資料降維後視覺化等。
PCA把原先的n個特徵用數目更少的m個特徵取代,新的m個特徵一要保證最大化樣本方差,二保證相互獨立的。新特徵是舊特徵的線性組合,提供一個新的框架來解釋結果。接下來分四部分來展開PCA的理論與實踐:
• 什麼時候用PCA,即資料特點;
• 什麼是主成分分析、主成分計算;
• 主成分分析為什可以,即主成分理論基礎;
• python如何快速實現PCA;
一、資料特點
1.維度災難
維度災難,簡單來說就是變數的個數多。如果變數個數增加,隨之需要估計的引數個數也在增加,在訓練集保持不變的情況下待估引數的方差也會隨之增加,導致引數估計質量下降。
2.變數關係不一般。
變數關係不一般,指的是變數彼此之間常常存在一定程度的、有時甚至是相當高的相關性,這說明資料是有冗餘的,或者說觀測資料中的資訊是有重疊的,這是我們利用主成分進行降維的前提條件,也可以說這使得變數降維成為可能(觀察變數的相關係數矩陣,一般來說相關係數矩陣中多數元素絕對值大於0.5,非常適合做主成分分析,但也不是說小於的就不可以用這種方法)。
在變數個數多,相互的相關性比較大的時候,我們會不會去尋找變數中的“精華”呢?,尋找個數相對較少的綜合變數呢?這是我們利用主成分降維的動機。
可參考被博文廣傳的例子:
•比如拿到一個汽車的樣本,裡面既有以“千米/每小時”度量的最大速度特徵,也有“英里/小時”的最大速度特徵,顯然這兩個特徵有一個多餘。
• 拿到一個數學系的本科生期末考試成績單,裡面有三列,一列是對數學的興趣程度,一列是複習時間,還有一列是考試成績。我們知道要學好數學,需要有濃厚的興趣,所以第二項與第一項強相關,第三項和第二項也是強相關。那是不是可以合併第一項和第二項呢?
二、什麼是主成分分析
1.由來:
主成分分析(principal component analysis)由皮爾遜(Pearson,1901)首先引入,後來被霍特林(Hotelling,1933)發展了。
2. 描述;
主成分分析是一種通過降維技術把多個變數化為少數幾個主成分(綜合變數)的統計分析方法。這些主成分能夠反映原始變數的絕大部分資訊,它們通常表示為原始變數的某種線性組合。
那為了主成分的為了是這些主成分所含的資訊不互相重疊,應要求他們之間互不相關。
主成分的目的:
(1)變數的降維
(2)主成分的解釋(在主成分有意義的情況下)
3.計算步驟
例子:我們簡單粗暴直接上例子,我們帶著問題看例子,一步一步來。(例子來自《應用多元統計》,王學民老師著)
在制定服裝標準的過程中,對128名成年男子的身材進行了測量,每人測得的指標中含有這樣六項:身高(x1)、坐高(x2) 、胸圍(x3) 、手臂長(x4) 、肋圍(x5)和腰圍(x6) 。
第一步,對原始資料標準化(減去對應變數的均值,再除以其方差),並計算相關矩陣(或協方差矩陣):
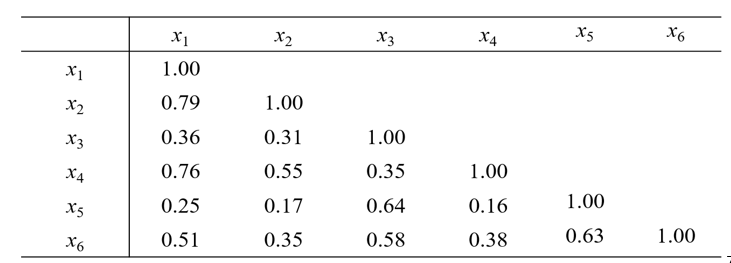
第二步,計算相關矩陣的特徵值及特徵向量。
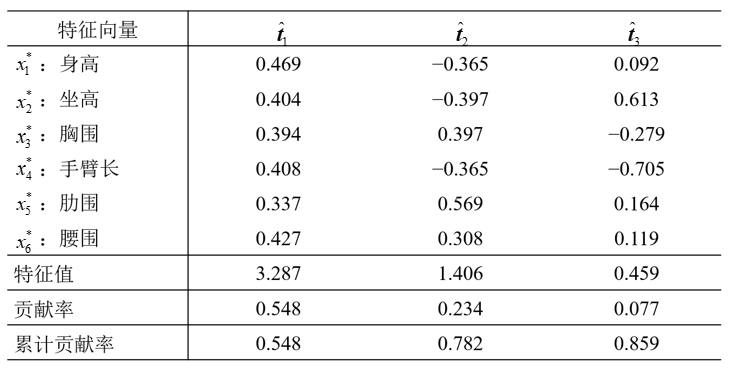
特徵值從大到小排列,特徵向量和特徵值對應從大到小排列。前三個主成分分別為:
第三步,根據累計貢獻率(一般要求累積貢獻率達到85%)可考慮取前面兩個或三個主成分。
第四步,解釋主成分。觀察係數發現第一主成分系數多為正數,且變數都與身材大小有關係,稱第一主成分為(身材)大小成分;類似分析,稱第二主成分為形狀成分(或胖瘦成分),稱第三主成分為臂長成分。
(結合一定的經驗和猜想,解釋主成分,不是所有的主成分都能被合理的解釋)
稱第一主成分為(身材)大小成分,稱第二主成分為形狀成分(或胖瘦成分),稱第三主成分為臂長成分。
可考慮取前兩個主成分。
由於
第五步,計算主成分得分。即對每一個樣本資料標準化後帶入第三步的主成分公式中,計算第一主成分得分,第二主成分得分。
第六步,將主成分可畫圖聚類,將主成分得分看成新的因變數可線性迴歸。
例子參考《多元統計分析》王學民老師著,上海財經大學出版社
總結一下PCA的演算法步驟:
設有m條n維資料,m個樣本,對原始資料標準化(減去對應變數的均值,再除以其方差),每個樣本對應p個變數,
1.求出自變數的協方差矩陣(或相關係數矩陣);
2.求出協方差矩陣(或性關係數矩陣)的特徵值及對應的特徵向量;
3.將特徵向量按對應特徵值大小從上到下按行排列成矩陣,取前k行組成矩陣
4.Y=
5.可將每個樣本的主成分得分畫散點圖及聚類,或將主成分得分看成新的因變數,對其做線性迴歸等。
4.主成分的應用
在主成分分析中,我們首先應保證所提取的前幾個主成分的累計貢獻率達到一個較高的水平,其次對這些被提取的主成分都能夠給出符合實際背景和意義的解釋。但是主成分的解釋其含義一般多少帶有點模糊性,不像原始變數的含義那麼清楚、確切,這是變數降維過程中不得不付出的代價。因此,提取的主成分個數m通常應明顯小於原始變數個數p(除非p本身較小),否則主成分維數降低的“利”,可能抵不過主成分含義不如原始變數清楚的“弊”。
在一些應用中,這些主成分本身就是分析的目的,此時我們需要給前幾個主成分一個符合實際背景和意義的解釋,以明白其大致的含義。
在更多的另一些應用中,主成分只是要達到目的的一箇中間結果(或步驟),而非目的本身。例如,將主成分用於聚類(主成分聚類)、迴歸(主成分迴歸)、評估正態性、尋找異常值,以及通過方差接近於零的主成分發現原始變數間的多重共線性關係等,此時的主成分可不必給出解釋。
三、主成分為什麼可以?(主成分的原理)
小節內容有:.PCA理論基礎:方差最大理論、方差最大和協方差的關係、解釋方差最大和主成分的關係、貢獻率和累計貢獻率概念、主成分取多少個呢?、幾何意義。
經過主成分在壓縮資料之後的資料(主成分得分資料),多個變數變為更少的綜合變數,變數個數減少了,還能反映原有資料的資訊嗎?答案是可以的。為什麼可以呢?解決以上疑問前我們需要了解PCA理論基礎:
1.PCA理論基礎:方差最大理論
我們以一個二維資料為例:
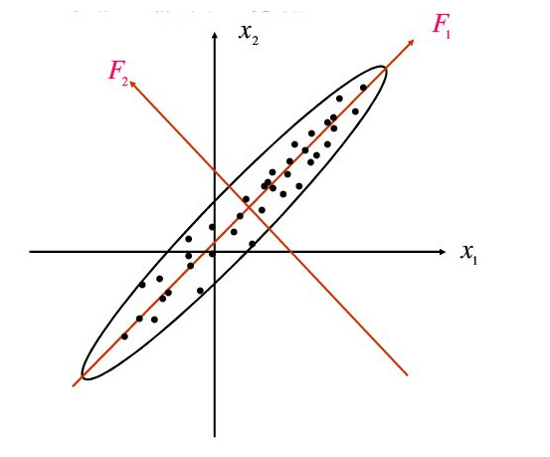
圖1:尋找主成分的正交旋轉
將二維,降至一維
• a二維經過投影,變為一維;
• b要儘可能保留原始資訊。直觀的感受就是投影之後儘量分散,點分佈差異相對較大,沒有相關性。(相反的極端情況是投影后聚成一團,變數間的差別小,蘊含的資訊就少了)所以樣本間有變化,才有更多資訊,變化就是差異;
• c如何體現差異呢?,可量化的方差。這就需要找一個方向使得投影后它們在投影方向上的方差儘可能達到最大,即在此方向上所含的有關原始資訊樣品間的差異資訊是最多的;
• d
