搞懂間隔

  給定訓練樣本集D={(x1,y1),(x2,y2),...,(xm,ym)},yi∈{−1,+1}$D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\},y_i\in \{-1,+1\}$，分類學習最基本的想法就是基於訓練集D$D$在樣本空間中找到一個劃分超平面，將類別分開。如下圖所示。

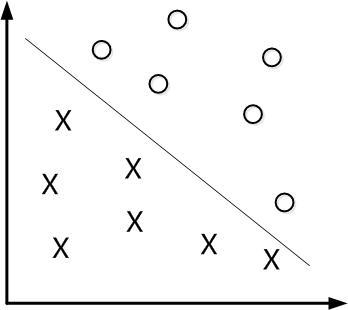
  但是能將樣本分開的超平面有很多，直觀上看，應該找兩類訓練樣本“正中間”的超平面，讓兩類“相離”最遠。

  超平面可通過如下線性方程來描述：

wTx+b=0,$$w^{T}x+b=0,$$
  其中w=(w1;w2;...;wd)$w=(w_1;w_2;...;w_d)$為超平面法向量，決定超平面的方向；b為位移項，決定超平面與原點之間的距離。

  超平面記為

(w,b)$(w,b)$，接下來說明所謂的“間隔”。

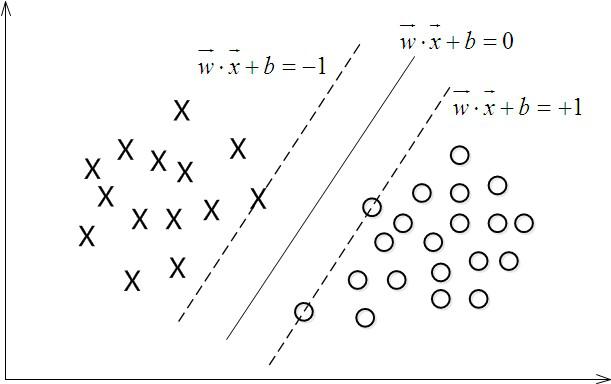
  如上圖，中間的實現表示的為超平面(w,b)$(w,b)$，假設超平面能正確分類，即對於(xi,yi)∈D$(x_i,y_i)\in D$，若yi=+1$y_i=+1$，則有wTx+b>0$w^{T}x+b>0$；若yi=−1$y_i=-1$，則有wTx+b<0$w^{T}x+b<0$。令 {wTx+b≥+1,wTx+b≤−1,yi=+1yi=−1$$\{\begin{array}{cc}{w}^{T}x+b\ge +1,& y_i=+1\\ w^{T}x+b\le -1,& y_i=-1\end{array}$$

  在上圖中，距離超平面最近的這幾個樣本點使得上式的等號成立，它們就被稱為支援向量。兩個異類支援向量到超平面之間的距離之和，就是我們要找的間隔。

  間隔有函式間隔和幾何間隔，先講函式間隔，設

f(x)=wTx+b$f(x)=w^{T}x+b$，在超平面w*x+b=0確定的情況下，|w∗x+b|$|w\ast x+b|$ 能夠表示點x到距離超平面的遠近，而通過觀察 w∗x+b$w\ast x+b$ 的符號與類標記y的符號是否一致可判斷分類是否正確，所以，可以用(y∗(w∗x+b))$(y\ast (w\ast x+b))$的正負性來判定或表示分類的正確性。於此，我們便引出了函式間隔（functional margin）的概念。

  定義函式間隔（用γˆ$\hat{\gamma }$表示）為：

γˆ=y(wTx+b)=yf(x)$$\hat{\gamma }=y(w^{T}x+b)=yf(x)$$

  γˆ$\hat{\gamma }$越大，代表可信度越高，但是函式間隔有問題，假如同時增大w，b到k倍$w，b到k倍$，超平面沒有變，但是間隔函式值卻改變了。

  事實上，我們可以對法向量w加些約束條件，從而引出真正定義點到超平面的距離–幾何間隔（geometrical margin）的概念，

  樣本空間中任意一點x$x$到超平面(w,b)$(w,b)$的距離用 γ$\gamma$ 表示，根據幾何知識，上圖中有

相關推薦

搞懂SVM的三個問題，間隔，對偶問題，KKT條件

搞懂間隔   給定訓練樣本集D={(x1,y1),(x2,y2),...,(xm,ym)},yi∈{−1,+1}D={(x1,y1),(x2,y2),...,(xm,ym)},yi∈{−1,+1}，分類學習最基本的想法就是基於訓練集DD在樣本空間中找到一個劃分

EOS 上線前，先搞懂這兩個基本概念

EOS 區塊鏈 區塊鏈技術 如果你曾經嘗試在本地運行 EOS 測試節點，會發現編譯、運行並不是特別復雜，但官方教程裏兩個概念很容易把人搞暈： Account（賬戶）和 Wallet （錢包）。 EOS 的 Wallet 跟其他區塊鏈項目是類似的，都是一個基本功能：本地儲存密鑰，僅此而已。你可能說了

讀懂這三個關鍵詞，就明白迅雷鏈為什麼受開發者歡迎

作為一條底層主鏈，迅雷鏈的快速崛起簡直不可思議。一方面，主鏈是整個行業最為擁擠的賽道，調查資料顯示，目前區塊鏈有5000個公鏈，比國內有註冊的區塊鏈開發工程師人數還要多幾倍。同時，主鏈面臨的競爭也很激烈，國內有的是起步早、團隊大的主鏈專案，其中很有幾個在世界範圍都比較知名的專案，遑論還有自帶大神光環

總結javascript基礎概念系列計劃分為三個部分：作用域，事件循環，原型鏈。

嚴格模式 增加 throw 相互 語法錯誤 第一個 scope val 分析 主要問題： 1、javaScript代碼的編譯和執行過程，詞法作用域規則？2、this的動態綁定方式有幾種？3、全局和函數之外是不是還有其他的作用域？4、為什麽代碼規範多禁止with、eval?

SQL有三個類型的索引，唯一索引 不能有重復，但聚集索引，非聚集索引可以有重復

返回 自動添加 post 設置 span 唯一索引 tca lock 所有 重要： (1) SQL如果創建時候，不指定類型那麽默認是非聚集索引 (2) 聚集索引和非聚集索引都可以有重復記錄，唯一索引不能有重復記錄。 (3) 主鍵 默認是加了唯一約束的聚集索引，但是也可

學習嵌入式技術開發難得不難，看你自己怎麽規劃？三個月幫助你成功，0基礎可學

嵌入式 就業規劃學IT技術，找好工作，就來信盈達。信盈達中國IT培訓實力機構，辦學10年，已經培養IT技術人才20萬。 信盈達IT培訓現可“先學習，後付款“，名額有限，趕快咨詢微信/電話：1/7/7/2/7/6/5/9/3/0/3，如果你想學技術改變現狀，這是一個機會。深圳信盈達嵌入式技術實訓學院已有10年

js中三個默認方法call，applay，bind

數據類型 div IV argument use 組類型 事件 實參 cti 這三個都是函數自帶的方法（Function.prototype），這三個方法都能夠改變函數內部 this的指向， call //call方法接收三個參數，第一個是this指向，第二個，三個

es6 陣列例項的 entries() ， keys() 和 values() ES6 提供三個新的方法 —— entries()，keys()和values() —— 用於遍歷陣列。它們都返回一個遍歷器物件，可以用for...of迴圈進行遍歷，唯一的區別是keys()是對鍵名的遍歷、values(

ES6 提供三個新的方法 —— entries()，keys()和values() —— 用於遍歷陣列。它們都返回一個遍歷器物件，可以用for...of迴圈進行遍歷，唯一的區別是keys()是對鍵名的遍歷、values()是對鍵值的遍歷，entries()是對鍵值對的遍歷

這三個網站太強大了，沒有找不到的資源

不知道大家有沒有這樣的經歷。想搜尋某一樣東西的時候，開啟一款搜尋引擎，經過長時間的瀏覽，得到的結果卻不如人意。今天就告訴大家這三款神奇又好用的搜尋資源網站，讓你沒有找不到的資源。   一、Google www.google.cn   一款可

一文徹底搞懂卷積神經網路的“感受野”，看不懂你來找我！

  一、什麼是“感受野” 1.1 感受野的概念 “感受野”的概念來源於生物神經科學，比如當我們的“感受器”，比如我們的手受到刺激之後，會將刺激傳輸至中樞神經，但是並不是一個神經元就能夠接受整個面板的刺激，因為面板面積大，一個神經元可想而知肯定接受不完，而且我們同

設計一個包含一個interface，三個class的Java 程式，用於完成陣列排序排序任務。其中interface中包含一個sort() 方法。第一個class使用氣泡排序法實現interface的

題目：設計一個包含一個interface，三個class的Java 程式，用於完成陣列排序排序任務。其中interface中包含一個sort() 方法。第一個class使用氣泡排序法實現interface的sort()方法;第二個class使用選擇排序法實現interface的sort()方法;

如何在不借助其他函式和第三個變數的情況下，更換兩個變數的值？

如題，這是一個有趣的小題目。具體方法如下： ▍方法一 var a = 3; var b = 4; a = a + b; // 7 b = a - b; // 3 a = a - b; /

輸入三個整數x,y,z，請把這三個數由大到小輸出

輸入三個整數x,y,z，請把這三個數由大到小輸出 x = int(input('第一個整數x：')) y = int(input('第二個整數x：')) z = int(input('第三個整數x：')) # f方法1 max = x if y > x: if y >

辛苦培養三個月的程式設計師，說走就走，領導：罵幾句就離職，無語了，網友：你憑什麼罵人

最近在網上流傳這樣一句話：不要大聲責罵年輕人，他們會立刻辭職的，但是你可以往死裡罵那些中年人，尤其是有車有房有娃的那些。看到這句話似乎並不合理，罵人也要分物件？然而在職場上這種現象確實存在。年輕人沒有什麼壓力，又是血氣方剛的年紀，幹得不爽立馬辭職，而中年人就不一樣了，有房有車要養，還要帶娃，辭職會斷

python中輸入三個整數x,y,z，請把這三個數由小到大輸出。

輸入三個整數x,y,z，請把這三個數由小到大排序,再把陣列由大到小排序，再輸出最大值和最小值！ #定義一個空陣列 numbers = [] #迴圈遍歷，下面的4是控制迴圈次數 for i in range(4): if i > 0: x = int(input(f"請輸入

網路程式設計的三個重要訊號（SIGHUP ，SIGPIPE，SIGURG）

　　對於訊號的介紹，我再前面的一篇部落格中做過專門的總結，感興趣的可以看看。本文主要介紹在網路程式設計中幾個密切相關的函式：SIGUP，SIGPIPE，SIGURG。 SIGHUP訊號 　　在介紹SIGHUP訊號之前，先來了解兩個概念：程序組和會話。

終於搞懂了什麼是二叉查詢樹，AVL樹，B樹，B+樹，紅黑樹

二叉查詢樹： 二叉查詢樹就是左結點小於根節點，右結點大於根節點的一種排序樹，也叫二叉搜尋樹。也叫BST，英文Binary Sort Tree。 二叉查詢樹比普通樹查詢更快，查詢、插入、刪除的時間複雜度為O（logN）。但是二叉查詢樹有一種極端的情況，就是會變成一種線性連結

【c】請輸入三個大於零的數字，判斷是否能構成三角形 ，若能，請求出三角形的面積；若不能，輸出結果。

//例3.4拓展延伸題目 //請輸入三個大於零的數字，判斷是否能構成三角形 ，若能，請求出三角形的面積；若不能，輸出結果。 #include<stdio.h> #include<math.h> int main() { double s,ar

函式計算兩個時間間隔年數，月數，天數

DATA:T_DAYS type I, T_MONTHS type I, T_YEARS type I.CALL FUNCTION 'FIMA_DAYS_AND_MONTHS_AND_YEARS'   EXPORTING     I_DATE_FROM = '20120201'     I_DATE_TO  

Shiro框架中有三個核心概念：Subject ，SecurityManager和Realms。

2.1.2    SecurityManagerSubject的“幕後”推手是SecurityManager。Subject代表了當前使用者的安全操作，SecurityManager則管理所有使用者的安全操作。它是Shiro框架的核心，充當“保護傘”，引用了多個內部巢狀安全元件，它們形成了物件圖。但是，一旦S