實戰06 頂天立地,三分天下——支援向量機SVM
SVM有三寶:間隔,對偶,核技巧。
軟間隔鬆弛變數(
) or 懲罰因子( C)
核函式與鬆弛變數: 一般的過程應該是這樣,還以文字分類為例。在原始的低維空間中,樣本相當的不可分,無論你怎麼找分類平面,總會有大量的離群點,此時用核函式向高維空間對映一下,雖然結果仍然是不可分的,但比原始空間裡的要更加接近線性可分的狀態(就是達到了近似線性可分的狀態),此時再用鬆弛變數處理那些少數“冥頑不化”的離群點,就簡單有效得多啦。
——————————————————————————————
一 分隔超平面
- 將資料集分隔開來的物件叫做分隔超平面,寫成 。特別地,二維平面的分隔超平面是直線。
- 尋找離分隔超平面最近的點,確保它們離分隔面的距離儘可能遠。這裡點到分隔面的距離被稱為間隔(margin)。
- 支援向量(support vector)就是離分隔超平面最近的那些點。
二 最大間隔
分類器輸出的是類別標籤,這裡輸出的是{+1, -1}
目標:尋找分類器定義中的 w 和 b。
第一步就是尋找支援向量,而滿足 >0時,則為支援向量。
-
最大化間隔的公式如下:

-
優化目標(對偶問題):
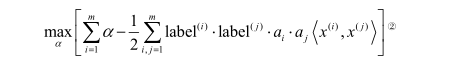
尖括號表示內積。 -
其約束條件為:
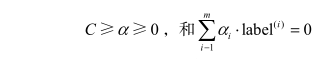
三 SMO演算法
目標:求出一些列的 和b(進而可得到w),有了w和b就可以得到超平面。
原理:(由約束條件)每次迴圈中選擇兩個 進行優化,並固定其他。因為累加和為0,因此,優化過程中一個增大,一個必須減小。<內迴圈、外迴圈>
清單6-2 如何判斷正間隔還是負間隔?(存疑)
numpy陣列過濾 如:alphas[alphas>0]
優化加速:選擇最大步長
迴圈計算cache列表中的預測誤差,並返回使誤差變化量最大的下標maxK 和最大誤差值Ej。
計算w
smoP(…)返回b和 alphas後,根據對偶問題中的公式:
四 核技巧
核函式(kernel)的工具將資料轉換成易於分類器理解的形式。將低維特徵空間對映到高維空間。 其中,徑向基函式(radial basis function)是最流行的二分類的核函式。
將內積替換成核函式的方式,稱為核技巧。
- 徑向基函式高斯版本中, 是使用者定義的到達率(reach)或者說是函式值跌落到0的速度引數。
- 線性核函式中,內積計算實在“所有資料集X” 和“資料集中的一行X[i, :]”這兩個輸入中展開。
numpy矩陣中,除法指對矩陣元素展開計算,而不是matlab中的求逆。