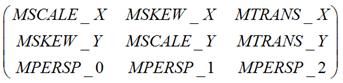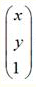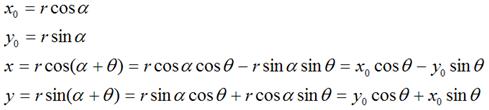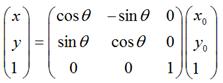1 概述

這裡我們會詳細講解matrix的各個方法，以及它的用法。matrix叫做矩陣，在前面講解 ColorFilter 的文章中，我們講解了ColorMatrix，他是一個4*5的矩陣。而這裡，我們講解的Matrix不是用於處理顏色的，而是處理圖形的。他是一個3*3的矩陣。

2 原理

先看看matrix的矩陣是什麼樣子的：

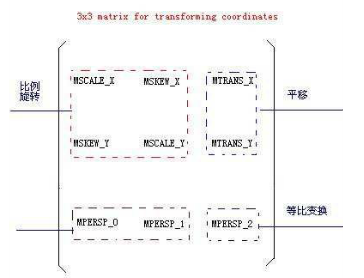
這裡可以檢視Matrix的程式碼得到。那麼這個矩陣分別代表了什麼呢，這裡通過他們的名字可以看出，scale是縮放，skew是錯切（canvas變換中有講過），trans是平移，persp代表透視（官方文件中，也沒有詳細講解，透視在這裡只做簡單介紹）。這裡需要把矩陣根據他們的作用劃分為4塊：

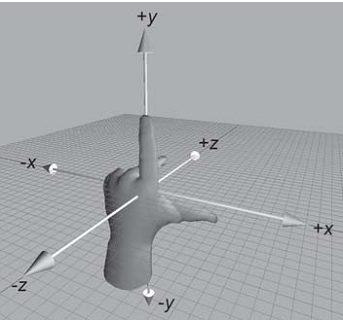
如上圖所示，這四塊區域各有作用。後面會詳細講解各個作用，先來看看這個矩陣是如何影響影象的。先看看螢幕的座標系：

看上圖，這裡表示了螢幕的座標系，其中的x，y軸是大家所熟知的，但是其實，一個物體他是存在於一個三維空間的，所以必然會有z軸。我們的螢幕，就像是一個視窗，透過它，我們看到了屏幕後面的世界，那裡面有各種物體，我們看到的是對映在x，y平面上的一個投射影象。螢幕就像是一個鏡頭一樣，將裡面的物體對映到x，y平面上，成為一個二維的影象。那麼如果，我們把螢幕這個鏡頭沿著z軸，拉遠或者拉進，那麼影象會有什麼變化呢，肯定會變小或者變大。就好比坐在飛機上透過視窗看地面的汽車，和在地面上看到的大小是不同的。

結論就是，在螢幕上顯示的畫素，不僅僅有x，y座標，其實還有z軸的影響。所以這裡對應的畫素描述由一個3行一列的矩陣來表示：

x，y分別代表x，y軸上的座標，而1代表螢幕在z軸上的座標為預設的。如果將1變大，那麼螢幕會拉遠， 圖形會變小。

現在我們來看看matrix怎麼作用於每個畫素的值。這裡需要用到矩陣的乘法，首先需要明確的是，矩陣的前乘和後乘是不相同的，也就是說不滿足乘法交換律。

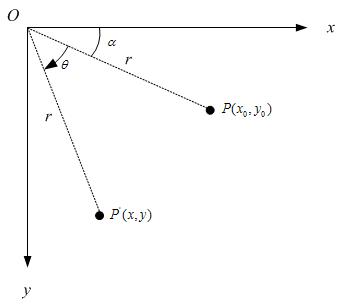
這裡我們通過一個旋轉變換來看看原理,其實一張圖片圍繞一個點旋轉，也就是所有的點都圍繞一個點旋轉，所以只需要關注一個點的情況即可：

假定有一個點 ，相對座標原點順時針旋轉後的情形，同時假定P點離座標原點的距離為r，如下圖：

那麼就有：

換做矩陣運算就如下圖：

從這裡就可以看出，矩陣中的值，是如何作用於畫素點的x，y座標以及z軸遠近。

同時，可以看到，上面的矩陣四塊區域的切分也是因為矩陣乘法的操作決定的，由於這裡的乘法運算中，左上角的四個值，可以和x，y值做乘法運算，所以可以影響到旋轉等操作，而右上角的模組，只能做加法，所以只能影響到平移。右下角的模組主要管z軸，自然就可以進行等比的縮放了，左下角的模組一般不去動他，否則會把x，y值加入到z軸中來，會不可控。

3 基本方法解析

講解完了matrix作用於畫素點的原理之後，我們逐個講解它的方法。

(1) 建構函式

public Matrix()
public Matrix(Matrix src)

• 1
• 2
• 3

建構函式有兩個，第一個是直接建立一個單位矩陣，第二個是根據提供的矩陣建立一個新的矩陣（採用deep copy）

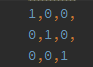
單位矩陣如下：

(2) isIdentity與isAffine

public boolean isIdentity()//判斷是否是單位矩陣
public boolean isAffine()//判斷是否是仿射矩陣

• 1
• 2
• 3

是否是單位矩陣很簡單，就不做講解了，這裡是否是仿射矩陣可能大家不好理解。

首先來看看什麼是仿射變換。仿射變換其實就是二維座標到二維座標的線性變換，保持二維圖形的“平直性”（即變換後直線還是直線不會打彎，圓弧還是圓弧）和“平行性”（指保持二維圖形間的相對位置關係不變，平行線還是平行線，而直線上點的位置順序不變），可以通過一系列的原子變換的複合來實現，原子變換就包括：平移、縮放、翻轉、旋轉和錯切。這裡除了透視可以改變z軸以外，其他的變換基本都是上述的原子變換，所以，只要最後一行是0,0,1則是仿射矩陣。

(3) rectStaysRect

public boolean rectStaysRect()

• 1
• 2

判斷該矩陣是否可以將一個矩形依然變換為一個矩形。當矩陣是單位矩陣，或者只進行平移，縮放，以及旋轉90度的倍數的時候，返回true。

(4) reset

public void reset()

• 1
• 2

重置矩陣為單位矩陣。

(5) setTranslate

public void setTranslate(float dx, float dy)

• 1
• 2

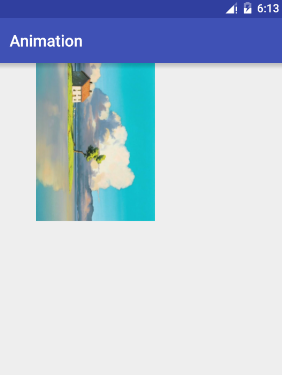
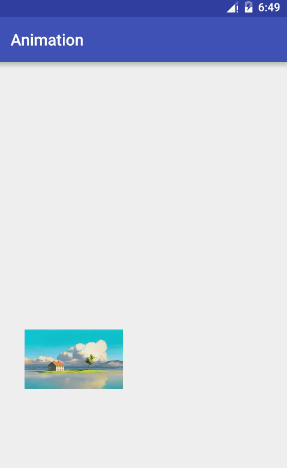
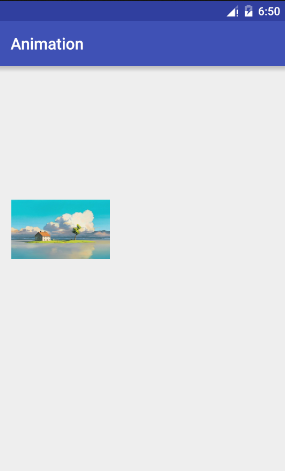
設定平移效果，引數分別是x，y上的平移量。
效果圖如下：

程式碼如下：

Matrix matrix = new Matrix();
canvas.drawBitmap(bitmap, matrix, paint);

matrix.setTranslate(100, 1000);
canvas.drawBitmap(bitmap, matrix, paint);

• 1
• 2
• 3
• 4
• 5

(6) setScale

public void setScale(float sx, float sy, float px, float py)
public void setScale(float sx, float sy)

• 1
• 2
• 3

兩個方法都是設定縮放到matrix中，sx，sy代表了縮放的倍數，px,py代表縮放的中心。這裡跟上面比較類似不做講解了。

(7) setRotate

 public void setRotate(float degrees, float px, float py)
 public void setRotate(float degrees)

• 1
• 2
• 3

和上面類似，不再講解。

(8) setSinCos

public void setSinCos(float sinValue, float cosValue, float px, float py)
public void setSinCos(float sinValue, float cosValue)

• 1
• 2
• 3

這個方法乍一看可能有點蒙，其實在前面的原理中，我們講解了一個旋轉的例子，他最終的矩陣效果是這樣的：

其實旋轉，就是使用了這樣的matrix，顯而易見，這裡的引數就清晰了。
sinValue：對應圖中的sin值
cosValue：對應cos值
px:中心的x座標
py：中心的y座標

看一個示例,我們把影象旋轉90度，那麼90度對應的sin和cos分別是1和0。

看程式碼如下：

Matrixmatrix = new Matrix();
matrix.setSinCos(1, 0, bitmap.getWidth() / 2, bitmap.getHeight() / 2);
canvas.drawBitmap(bitmap, matrix, paint);

• 1
• 2
• 3

(9) setSkew

public void setSkew(float kx, float ky, float px, float py)
public void setSkew(float kx, float ky)

• 1
• 2
• 3

錯切，這裡kx，ky分別代表了x，y上的錯切因子，px，py代表了錯切的中心。不瞭解錯切了在前面canvas變換中去檢視，這裡不再講解。

(10) setConcat

public boolean setConcat(Matrix a,Matrix b)

• 1
• 2

將當前matrix的值變為a和b的乘積,它的意義在下面的 進階方法中來探討。

4 進階方法解析

上面的基本方法中，有關於變換的set方法都可以帶來不同的效果，但是每個set都會把上個效果清除掉，例如依次呼叫了setSkew,setTranslate，那麼最終只有setTranslate會起作用，那麼如何才和將兩種效果複合呢。Matrix給我們提供了很多方法。但是主要都是2類：

preXXXX:以pre開頭，例如preTranslate
postXXXX:以post開頭，例如postScale

他們分別代表了前乘，和後乘。看一段程式碼：

Matrix matrix = new Matrix();
matrix.setTranslate(100, 1000);
matrix.preScale(0.5f, 0.5f);

• 1
• 2
• 3

這裡matrix前乘了一個scale矩陣，換算成數學式如下：

從上面可以看出，最終得出的matrix既包含了縮放資訊也有平移資訊。
後乘自然就是matrix在後面，而縮放矩陣在前面，由於矩陣前後乘並不等價，也就導致了他們的效果不同。我們來看看後乘的結果：

可以看到，結果跟上面不同，並且這也不是我們想要的結果，這裡縮放沒有更改，但是平移被減半了，換句話說，平移的距離也被縮放了。所以需要注意前後乘法的關係。

來看看他們對應的效果圖：

前乘：

後乘：

可以明顯看到，後乘的平移距離受了影響。

瞭解清除了前後乘的意義，在使用的過程中，多個效果的疊加時，一樣要注意，否則效果達不到預期。

5 其他方法解析

matrix除了上面的方法外，還有一些其他的方法，這裡依次解析

(1) setRectToRect

public boolean setRectToRect(RectF src, RectF dst, ScaleToFit stf)

• 1
• 2

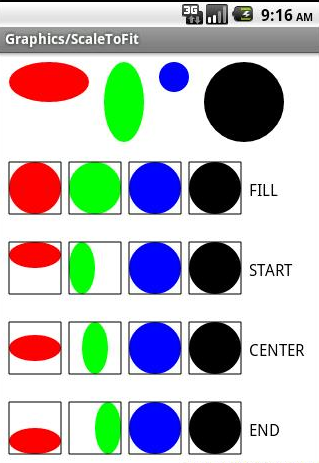
將rect變換成rect，上面的rectStaysRect已經說過，要保持rect只能做縮放平移和選擇90度的倍數，那麼這裡其實也是一樣，只是這幾種變化，這裡通過stf引數來控制。

ScaleToFit 有如下四個值：

FILL: 可能會變換矩形的長寬比，保證變換和目標矩陣長寬一致。
START:保持座標變換前矩形的長寬比，並最大限度的填充變換後的矩形。至少有一邊和目標矩形重疊。左上對齊。
CENTER: 保持座標變換前矩形的長寬比，並最大限度的填充變換後的矩形。至少有一邊和目標矩形重疊。
END:保持座標變換前矩形的長寬比，並最大限度的填充變換後的矩形。至少有一邊和目標矩形重疊。右下對齊。

這裡使用谷歌的api demo的圖片作為例子：

(2) setPolyToPoly

public boolean setPolyToPoly(float[] src, int srcIndex,float[] dst, int dstIndex,int pointCount)

• 1
• 2

通過指定的0-4個點，原始座標以及變化後的座標，來得到一個變換矩陣。如果指定0個點則沒有效果。

下面通過例子分別說明1到4個點的可以達到的效果：

這裡寫程式碼片##### 1個點，平移
只指定一個點，可以達到平移效果：

程式碼如下：

float[] src = {0, 0};
int DX = 300;
float[] dst = {0 + DX, 0 + DX};
matrix.setPolyToPoly(src, 0, dst, 0, 1);
canvas.drawBitmap(bitmap, matrix, paint);

• 1
• 2
• 3
• 4
• 5

2個點，旋轉或者縮放

兩個點，可以達到旋轉效果或者縮放效果，縮放比較簡單，這裡我們來看旋轉效果，一個點指定中心，一點指出旋轉的效果

程式碼如下

int bw = bitmap.getWidth();
int bh = bitmap.getHeight();
float[] src = {bw / 2, bh / 2, bw, 0};
float[] dst = {bw / 2, bh / 2, bw / 2 + bh / 2, bh / 2 + bw / 2};
matrix.setPolyToPoly(src, 0, dst, 0, 2);
canvas.drawBitmap(bitmap, matrix, paint);

• 1
• 2
• 3
• 4
• 5
• 6

圖片的中心點作為旋轉的中心，前後不變，右上角變化到了下方，所以導致圖片旋轉了90度。

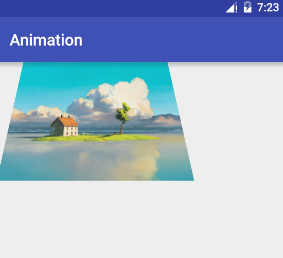
3個點，錯切

使用3個點，可以產生錯切效果，指定3個頂點，一個固定，另外兩個移動。

看圖：

程式碼如下：

Matrix matrix = new Matrix();
int bw = bitmap.getWidth();
int bh = bitmap.getHeight();
float[] src = {0,0, 0, bh,bw,bh};
float[] dst = {0, 0, 200, bh, bw + 200, bh};
matrix.setPolyToPoly(src, 0, dst, 0, 3);
canvas.drawBitmap(bitmap, matrix, paint);

• 1
• 2
• 3
• 4
• 5
• 6
• 7

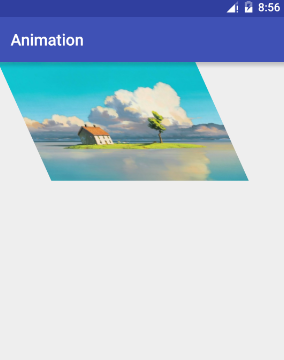
4個點，透視

透視就是觀察的角度變化了。導致投射到平面上的二維影象變化了。

我們看下面的例子，更容易理解：

圖片看起來好像傾斜了，實現特別簡單：

Matrix matrix = new Matrix();
int bw = bitmap.getWidth();
int bh = bitmap.getHeight();
float[] src = {0, 0, 0, bh, bw, bh, bw, 0};
int DX = 100;
float[] dst = {0 + DX, 0, 0, bh, bw, bh, bw - DX, 0};
matrix.setPolyToPoly(src, 0, dst, 0, 4);
canvas.drawBitmap(bitmap, matrix, paint);

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8

可以看到，只是把左右兩個頂點往裡面收攏了，這樣就得出了一個有3d效果的透檢視。

(3) invert

public boolean invert(Matrix inverse)

• 1
• 2

反轉當前矩陣，如果能反轉就返回true並將反轉後的值寫入inverse，否則返回false。當前矩陣*inverse=單位矩陣。

反轉前後有什麼效果，我們來看看示例：

可以看到，反轉之後，其實是對效果的一種反轉。

(4) mapPoints

public void mapPoints(float[] dst, int dstIndex, float[] src, int srcIndex,int pointCount)
public void mapPoints(float[] dst, float[] src)
public void mapPoints(float[] pts)

• 1
• 2
• 3
• 4

對映點的值到指定的陣列中，這個方法可以在矩陣變換以後，給出指定點的值。
dst：指定寫入的陣列
dstIndex：寫入的起始索引，x，y兩個座標算作一對，索引的單位是對，也就是經過兩個值才加1
src：指定要計算的點
srcIndex：要計算的點的索引
pointCount：需要計算的點的個數，每個點有兩個值，x和y。

(5) mapVectors

public void mapVectors(float[] dst, int dstIndex, float[] src, int srcIndex,int vectorCount)
public void mapVectors(float[] dst, float[] src)
public void mapVectors(float[] vecs)

• 1
• 2
• 3
• 4

與上面的mapPoionts基本類似，這裡是將一個矩陣作用於一個向量，由於向量的平移前後是相等的，所以這個方法不會對translate相關的方法產生反應，如果只是呼叫了translate相關的方法，那麼得到的值和原本的一致。

(6) mapRect

public boolean mapRect(RectF dst, RectF src)
public boolean mapRect(RectF rect)

• 1
• 2
• 3

返回值即是呼叫的rectStaysRect()，這個方法前面有講過，這裡把src中指定的矩形的左上角和右下角的兩個點的座標，寫入dst中。

(7) mapRadius

public float mapRadius(float radius)

• 1
• 2

返回一個圓圈半徑的平均值，將matrix作用於一個指定radius半徑的圓，隨後返回的平均半徑。

以上基本解析完畢了所有matrix的方法，以及一些高階用法，本篇文章就到這裡