目前網路上關於反向傳播演算法的教程已經很多，那我們還有必要再寫一份教程嗎？答案是‘需要’。

為什麼這麼說呢？我們教員Sanjeev最近要給本科生上一門人工智慧的課，儘管網上有很多反向傳播演算法的教程，但他卻找不到一份令他滿意的教程，因此我們決定自己寫一份關於反向傳播演算法的教程，介紹一下反向傳播演算法的歷史背景、原理、以及一些最新研究成果。

PS：本文預設讀者具備一定的基礎知識（如瞭解梯度下降、神經網路等概念）。

一、什麼是反向傳播演算法？

反向傳播演算法是訓練神經網路的經典演算法。在20世紀70年代到80年代被多次重新定義。它的一些演算法思想來自於60年代的控制理論。

在輸入資料固定的情況下、反向傳播演算法利用神經網路的輸出敏感度來快速計算出神經網路中的各種超引數。

尤其重要的是，它計算輸出f對所有的引數w的偏微分，即如下所示：?f/?wi，f代表神經元的輸出，wi是函式f的第i個引數。引數wi代表網路的中邊的權重或者神經元的閾值，神經元的啟用函式具體細節並不重要，它可以是非線性函式Sigmoid或RELU。這樣就可以得到f相對於網路引數的梯度?f ，有了這個梯度，我們就可以使用梯度下降法對網路進行訓練，即每次沿著梯度的負方向（??f）移動一小步，不斷重複，直到網路輸出誤差最小。

在神經網路訓練過程中，我們需要注意的是，反向傳播演算法不僅需要準確計算梯度。還需要使用一些小技巧對我們的網路進行訓練。理解反向傳播演算法可以幫助我們理解那些在神經網路訓練過程中使用的小技巧。

反向傳播演算法之所以重要，是因為它的效率高。假設對一個節點求偏導需要的時間為單位時間，運算時間呈線性關係，那麼網路的時間複雜度如下式所示：O(Network Size)=O(V+E)，V為節點數、E為連線邊數。這裡我們唯一需要用的計算方法就是鏈式法則，但應用鏈式法則會增加我們二次計算的時間，由於有成千上萬的引數需要二次計算，所以效率就不會很高。為了提高反向傳播演算法的效率，我們通過高度並行的向量，利用GPU進行計算。

注：業內人士可能已經注意到在標準的神經網路訓練中，我們實際上關心的是訓練損失函式的梯度，這是一個與網路輸出有關的簡單函式，但是上文所講的更具有普遍意義，因為神經網路是可以增加新的輸出節點的，此時我們要求的就是新的網路輸出與網路超引數的偏微分。

二、問題設定

反向傳播演算法適用於有向非迴圈網路，為了不失一般性，非迴圈神經網路可以看做是一個多層神經網路，第t+1層神經元的輸入來自於第t層及其下層。我們使用f表示網路輸出，在本文中我們認為神經網路是一個上下結構，底部為輸入，頂部為輸出。

規則1：為了先計算出引數梯度，先求出 ?f/?u ，即表示輸出f對節點u的偏微分。

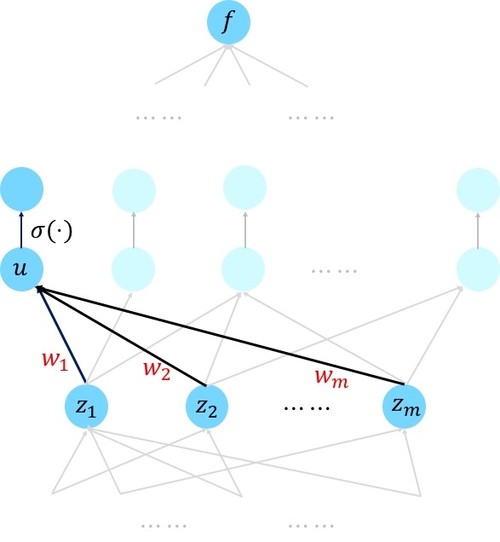
我們使用規則1來簡化節點偏微分計算。下面我將具體說一下?f/?u的含義。我們做如下假設，先刪除節點u的所有輸入節點。然後保持網路中的引數不變。現在我們改變u的值，此時與u相連的高層神經元也會受到影響，在這些高層節點中，輸出f也會受到影響。那麼此時?f/?u就表示當節點u變化時，節點f的變化率。

規則1就是鏈式法則的直接應用，如下圖所示，u是節點 z1,…,zm的加權求和，即u=w1*z1+?+wn*zn，然後通過鏈式法則對w1求偏導數，具體如下：

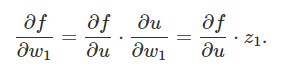
由上式所示，只有先計算?f/?u，然後才能計算?f/?w1。

多元鏈式法則

為了計算節點的偏微分，我們先回憶一下多元鏈式法則，多元鏈式法則常用來描述偏微分之間的關係。 即假設f是關於變數u1,…,un的函式，而u1,…,un又都是關於變數z的函式，那麼f關於z的偏導數如下：

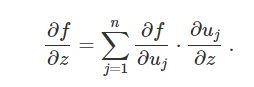
這是鏈式法則2的一般式，是鏈式法則的1的子式。這個鏈式法則很適合我們的反向傳播演算法。下圖就是一個符合多元鏈式法則的神經網路示意圖。

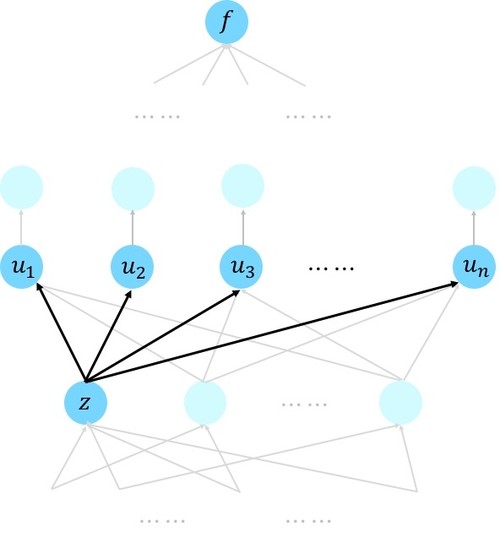
如上圖所示，先計算f相對於u1,…,un的偏導數，然後將這些偏導數按權重線性相加，得到f對z的偏導數。這個權重就是u1,…,un對z的偏導，即?uj/?z。此時問題來了，我麼怎麼衡量計算時間呢？為了與教課書中保持一致，我們做如下假設：u節點位於t+1層的，z節點位於t層或t層以下的子節點，此時我們記?u/?z的運算時間為單位時間。

樸素前饋演算法（低效演算法）

我們首先要指出鏈式法則是包含二次計算的時間。許多作者都不屑於講這種演算法，直接跳過的。這就好比我們在上演算法排序課時，老師都是直接講快速排序的，像那些低效排序演算法都是直接跳過不講的。

樸素演算法就是計算節點對ui與uj之間偏導數，在這裡節點ui的層級要比uj高。在V*V個節點對的偏導值中包含?f/?ui的值，因為f本身就是一個節點，只不過這個節點比較特殊，它是一個輸出節點。

我們以前饋的形式進行計算。我們計算了位於t層及t層以下的所有節點對之間的偏導數，那麼位於t+1層的ul對uj的偏導數就等於將所有ui與uj的偏導數進行線性加權相加。固定節點j，其時間複雜度與邊的數量成正比，而j是有V個值，此時時間複雜度為O(VE)。

三、反向傳播演算法（線性時間）

反向傳播演算法如其名所示，就是反向計算偏微分，資訊逆向傳播，即從神經網路的高層向底層反向傳播。

資訊協議：節點u通過高層節點獲取資訊，節點u獲取的資訊之和記做S。u的低階節點z獲取的資訊為S??u/?z

很明顯，每個節點的計算量與其連線的神經元個數成正比，整個網路的計算量等於所有節點運算時間之和，所有節點被計算兩次，故其時間複雜度為O(Network Size)。

我們做如下證明：S等於?f/?z。

證明如下：當z為輸出層時，此時?f/?z=?f/?f=1

假如對於t+1層及其高層假設成立，節點u位於t層，它的輸出邊與t+1層的u1,u2,…,um節點相連，此時節點從某個節點j收到的資訊為(?f/?uj)×(?uj/?z)，根據鏈式法則，節點z收到的總資訊為S=

四、自動微分

在上文中，關於神經網路、節點計算，我們並沒有細講。下面我們將具體講一下，我們將節點與節點之間的計算看做是一個無環圖模型，許多自動計算微分的工具包（如：autograd，tensorflow）均採用這一模型。這些工具就是通過這個無向圖模型來計算輸出與網路引數的偏導數的。

我們首先注意到法則1就是對這個的一般性描述，這個之所以不失一般性是因為我們可以將邊的權值也看做節點(即葉節點)。這個很容易轉換，如下圖所示，左側是原始網路，即一個單節點和其輸入節點、輸入節點的權重。右側是將邊的權重轉換為葉節點。網路中的其它節點也做類似轉換。

只要區域性偏導數計算的效率足夠高，那麼我們就可以利用上文所說的資訊協議來計算各個節點的偏微分。即對節點u來講，我們應該先找出它的的輸入節點有哪些，即z1,…,zn。然後計算在u的偏微分的基礎上計算zj的偏微分，由於輸出f對u的偏微分記做S，所以計算輸出f對zj的偏微分就是S??u?zj

這個演算法可以按照如下規則分塊計算，首先明確節點u與輸入節點z1,…,zn 的關係，然後就是怎麼計算偏導數的倍數（權重）S。即S??u/?zj。

擴充套件到向量空間：為了提高偏微分權重的計算效率，我們可以將節點的輸出也變為一個向量（矩陣或張量）。此時我們將?u/?zj?S改寫為?u/?zj[S], 這個與我們的反向傳播演算法思想是一致的，在反向傳播演算法中，y是一個p維向量，x是一個q維向量，y是關於x的函式，我們用?y/?x來表示由 ?yj/?xi所組成的q*p矩陣。聰明的讀者很快就會發現，這就是我們數學中的雅克比矩陣。此外我們還可以證明S與u的維度相同、?u?zj[S] 與zj的維度也相同。

如下圖所示，W是一個d2*d3的矩陣，Z是一個d1*d2的矩陣，U=WZ故U是一個d1*d3維的矩陣，此時我們計算?U/?Z，最終得到一個d2d3×d1d3維的矩陣。但我們在反向傳播演算法中，這個會算的很快，因為?U/?Z[S]=W?S，在計算機中我們可以使用GPU來進行類似向量計算。

五、重要知識擴充套件

1、權重共享

在許多神經網路框架中，設計者想要是一些神經元的引數能夠共享，這些引數包括邊的權重或者節點的閾值引數。例如，在卷積神經網路中，同一個卷集核使用的引數都是一樣的。簡而言之，就是a、b是兩個不同的引數，但我們強制要求a與b的值相同，即引數共享。這就好比我們給神經網路新增一個節點u，並且節點u與a和b相連，並且a=u，b=u.，此時根據鏈式法則，?f/?u=(?f/?a)?(?a/?u)+(?f/?b)?(?b/?u)=?f/?a+?f/?b. 因此，對一個共享引數而言，其梯度就是輸出與引數節點之間的中間節點的偏導數之和。

2、反向傳播演算法在迴圈神經網路的應用

上面我們講的是非迴圈神經網路，許多前沿應用（機器翻譯、語言理解）往往使用有向迴圈神經網路。在這種結構的神經網路中會存在記憶單元或注意力機制，在這些單元或機制中往往存在複雜的求導計算。一開始我們使用梯度下降法訓練網路，即在時間序列上對神經網路使用反向傳播演算法，即對這個有向環狀結構進行無限迴圈，每一次迴圈的網路結構、網路引數都是一樣的，但是網路的輸入與輸出是不一樣的。在實際應用中我們會遇到梯度爆炸或梯度消失等問題，這些都會對結果收斂產生影響。為了解決這些問題，我們使用梯度剪下或者長短記憶模型（LSTM）等技術解決上述問題。

環狀神經網路可以高效計算梯度的事實促進了有記憶網路甚至資料結構的發展。使用梯度下降法，我們可可以對環狀結構神經網路進行優化，尋找最佳引數，使得這個網路可以解決特定計算問題。梯度下降法的極限目前仍在探索中。

3、海森向量乘積計算耗時

在近似線性時間中，我們不僅可以使用梯度下降法，或許我們也可以使用2階導數對目標函式進行優化。在優化過程中，最關鍵的一步是計算海森矩陣與一個向量的積，下面我將向大家介紹如何在規模是O(Network size)的神經網路應用上述思想，這個例子與前面所講稍有不同，我們的初始神經網路應該是一個用反向傳播演算法進行簡單優化過的神經網路。

法則：假設在無環神經網路中，有V個節點，E條邊，網路輸出為f，葉節點為z1,…,zm，那麼必存在一個大小為O(V+E)的網路，這個網路的的輸入節點為z1,…,zm，輸出節點為?f/?z1,…,?f/?zm。

上面的定理可以通過在無環神經網路中實現訊息直接傳遞來證明，緊接著我們將解釋一下如何計算?2f(z)?v。設g(z)=??f(z),v? ，有定理可知， g(z)可以由大小是O(V+E)神經網路計算得到，同理我們再次應用法則，在這個大小是O(V+E)的網路計算g(z)的梯度，此時?g(z)=?2f(z)?v，此時我們就算出了海森矩陣與向量積的積，此時耗費的時間複雜度就是網路規模的大小。

以上便是BP學習過程中需要了解的一些內容，雷鋒網希望能讓你在學習過程中得到一個比較清晰的思路。當然，也歡迎你關注雷鋒網旗下公眾號“AI科技評論”與我們交流哦。

via Back-propagation, an introduction