「學習筆記」反向傳播Back Propagation

阿新 • • 發佈：2019-01-10

BackPropagation演算法是多層神經網路的訓練中舉足輕重的演算法。

簡單的理解，它的確就是複合函式的鏈式法則，但其在實際運算中的意義比鏈式法則要大的多。

背景知識

簡單表示式和理解梯度

從簡單表示式入手可以為複雜表示式打好符號和規則基礎。先考慮一個簡單的二元乘法函式 $f(x,y)=xy$ 。對兩個輸入變數分別求偏導數還是很簡單的：

$\displaystyle f(x,y)=xy \to \frac {df}{dx}=y \quad \frac {df}{dy}=x$

導數的意義：函式變數在某個點周圍的極小區域內變化，而導數就是變數變化導致的函式在該方向上的變化率。

$\frac{df(x)}{dx}= lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

注意等號左邊的分號和等號右邊的分號不同，不是代表分數。相反，這個符號表示操作符 $\frac{d}{dx}$ 被應用於函式 $f$

，並返回一個不同的函式（導數）。對於上述公式，可以認為 $h$ 值非常小，函式可以被一條直線近似，而導數就是這條直線的斜率。換句話說，每個變數的導數指明瞭整個表示式對於該變數的值的敏感程度。比如，若 $x=4,y=-3$ ，則 $f(x,y)=-12$ ， $x$ 的導數 $\frac{\partial f}{\partial x}=-3$ 。這就說明如果將變數 $x$ 的值變大一點，整個表示式的值就會變小（原因在於負號），而且變小的量是 $x$ 變大的量的三倍。通過重新排列公式可以看到這一點（ $f(x+h)=f(x)+h \frac{df(x)}{dx}$ ）。同樣，因為 $\frac{\partial f}{\partial y}=4$ ，可以知道如果將 $y$ 的值增加 $h$ ，那麼函式的輸出也將增加（原因在於正號），且增加量是 $4h$ 。

函式關於每個變數的導數指明瞭整個表示式對於該變數的敏感程度。

如上所述，梯度 $\nabla f$ 是偏導數的向量，所以有 $\nabla f(x)=[\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}]=[y,x]$ 。即使是梯度實際上是一個向量，仍然通常使用類似“x上的梯度

”的術語，而不是使用如“x的偏導數”的正確說法，原因是因為前者說起來簡單。

我們也可以對加法操作求導：

$\displaystyle f(x,y)=x+y \to \frac {df}{dx}=1\quad\frac {df}{dy}=1$

這就是說，無論其值如何， $x,y$ 的導數均為1。這是有道理的，因為無論增加 $x,y$ 中任一個的值，函式 $f$ 的值都會增加，並且增加的變化率獨立於 $x,y$ 的具體值（情況和乘法操作不同）。取最大值操作也是常常使用的：
$\displaystyle f(x,y)=max(x,y) \to \frac {df}{dx}=1 (x>=y) \quad\frac {df}{dy}=1 (y>=x)$

上式是說，如果該變數比另一個變數大，那麼梯度是1，反之為0。例如，若 $x=4,y=2$ ，那麼max是4，所以函式對於 $y$ 就不敏感。也就是說，在 $y$ 上增加 $h$ ，函式還是輸出為4，所以梯度是0：因為對於函式輸出是沒有效果的。當然，如果給 $y$ 增加一個很大的量，比如大於2，那麼函式 $f$ 的值就變化了，但是導數並沒有指明輸入量有巨大變化情況對於函式的效果，他們只適用於輸入量變化極小時的情況，因為定義已經指明： $lim_{h\to 0}$ 。

使用鏈式法則計算複合表示式

現在考慮更復雜的包含多個函式的複合函式，比如 $f(x,y,z)=(x+y)z$ 。雖然這個表達足夠簡單，可以直接微分，但是在此使用一種有助於讀者直觀理解反向傳播的方法。將公式分成兩部分： $q=x+y$ 和 $f=qz$ 。在前面已經介紹過如何對這分開的兩個公式進行計算，因為 $f$ 是 $q$ 和 $z$ 相乘，所以 $\displaystyle\frac{\partial f}{\partial q}=z,\frac{\partial f}{\partial z}=q$ ，又因為 $q$ 是 $x$ 加 $y$ ，所以 $\displaystyle\frac{\partial q}{\partial x}=1,\frac{\partial q}{\partial y}=1$ 。然而，並不需要關心中間量 $q$ 的梯度，因為 $\frac{\partial f}{\partial q}$ 沒有用。相反，函式 $f$ 關於 $x,y,z$ 的梯度才是需要關注的。鏈式法則指出將這些梯度表示式連結起來的正確方式是相乘，比如 $\displaystyle\frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial x}$ 。在實際操作中，這只是簡單地將兩個梯度數值相乘，示例程式碼如下：

# 設定輸入值
x = -2; y = 5; z = -4

# 進行前向傳播
q = x + y # q becomes 3
f = q * z # f becomes -12

# 進行反向傳播:
# 首先回傳到 f = q * z
dfdz = q # df/dz = q, 所以關於z的梯度是3
dfdq = z # df/dq = z, 所以關於q的梯度是-4
# 現在回傳到q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1. 這裡的乘法是因為鏈式法則
dfdy = 1.0 * dfdq # dq/dy = 1

最後得到變數的梯度[dfdx, dfdy, dfdz]，它們告訴我們函式f對於變數[x, y, z]的敏感程度。這是一個最簡單的反向傳播。一般會使用一個更簡潔的表達符號，這樣就不用寫df了。這就是說，用dq來代替dfdq，且總是假設梯度是關於最終輸出的。

這次計算可以被視覺化為如下計算線路影象：

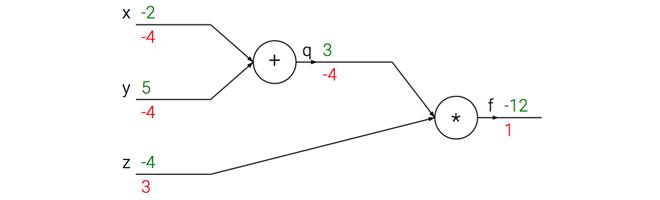
上圖的真實值計算線路展示了計算的視覺化過程。前向傳播從輸入計算到輸出（綠色），反向傳播從尾部開始，根據鏈式法則遞迴地向前計算梯度（顯示為紅色），一直到網路的輸入端。可以認為，梯度是從計算鏈路中迴流。

簡單理解

如下的神經網路

前向傳播

對於節點 $h_1$ 來說， $h_1$ 的淨輸入 $net_{h_1}$ 如下：
$net_{h_1}=w_1\times i_1+w_2\times i_2+b_1\times 1$
接著對 $net_{h_1}$ 做一個sigmoid函式得到節點 $h_1$ 的輸出：
$out_{h_1}=\frac{1}{1+e^{-net_{h_1}}}$
類似的，我們能得到節點 $h_2$ 、 $o_1$ 、 $o_2$ 的輸出 $out_{h_2}$ 、 $out_{o_1}$ 、 $out_{o_2}$ 。

誤差

得到結果後，整個神經網路的輸出誤差可以表示為：
$E_{total}=\sum\frac{1}{2}(target-output)^2$
其中 $output$ 就是剛剛通過前向傳播算出來的 $out_{o_1}$ 、 $out_{o_2}$ ； $target$ 是節點 $o_1$ 、 $o_2$ 的目標值。 $E_{total}$ 用來衡量二者的誤差。
這個 $E_{total}$ 也可以認為是cost function，不過這裡省略了防止overfit的regularization term（ $\sum{w_i^2}$ ）
展開得到
$E_{total}=E{o_1}+E{o_2}=\frac{1}{2}(target_{o_1}-out_{o_1})^2+\frac{1}{2}(target_{o_2}-out_{o_2})^2$

後向傳播

對輸出層的 $w_5$

通過梯度下降調整 $w_5$ ，需要求 $\frac{\partial {E_{total}}}{\partial {w_5}}$ ，由鏈式法則：
$\frac{\partial {E_{total}}}{\partial {w_5}}=\frac{\partial {E_{total}}}{\partial {out_{o_1}}}\frac{\partial {out_{o_1}}}{\partial {net_{o_1}}}\frac{\partial {net_{o_1}}}{\partial {w_5}}$ ，
如下圖所示：

$\frac{\partial {E_{total}}}{\partial {out_{o_1}}}=\frac{\partial}{\partial {out_{o_1}}}(\frac{1}{2}(target_{o_1}-out_{o_1})^2+\frac{1}{2}(target_{o_2}-out_{o_2})^2)=-(target_{o_1}-out_{o_1})$
$\frac{\partial {out_{o_1}}}{\partial {net_{o_1}}}=\frac{\partial }{\partial {net_{o_1}}}\frac{1}{1+e^{-net_{o_1}}}=out_{o_1}(1-out_{o_1})$
$\frac{\partial {net_{o_1}}}{\partial {w_5}}=\frac{\partial}{\partial {w_5}}(w_5\times out_{h_1}+w_6\times out_{h_2}+b_2\times 1)=out_{h_1}$
以上3個相乘得到梯度 $\frac{\partial {E_{total}}}{\partial {w_5}}$ ，之後就可以用這個梯度訓練了：
$w_5^+=w_5-\eta \frac{\partial {E_{total}}}{\partial {w_5}}$

很多教材比如Stanford的課程，會把中間結果 $\frac{\partial {E_{total}}}{\partial {net_{o_1}}}=\frac{\partial {E_{total}}}{\partial {out_{o_1}}}\frac{\partial {out_{o_1}}}{\partial {net_{o_1}}}$ 記做 $\delta_{o_1}$ ，表示這個節點對最終的誤差需要負多少責任。所以有 $\frac{\partial {E_{total}}}{\partial {w_5}}=\delta_{o_1}out_{h_1}$ 。

對隱藏層的 $w_1$

通過梯度下降調整 $w_1$ ，需要求 $\frac{\partial {E_{total}}}{\partial {w_1}}$ ，由鏈式法則：
$\frac{\partial {E_{total}}}{\partial {w_1}}=\frac{\partial {E_{total}}}{\partial {out_{h_1}}}\frac{\partial {out_{h_1}}}{\partial {net_{h_1}}}\frac{\partial {net_{h_1}}}{\partial {w_1}}$ ，

如下圖所示：

引數 $w_1$ 影響了 $net_{h_1}$ ，進而影響了 $out_{h_1}$ ，之後又影響到 $E_{o_1}$ 、 $E_{o_2}$ 。
求解每個部分：
$\frac{\partial {E_{total}}}{\partial {out_{h_1}}}=\frac{\partial {E_{o_1}}}{\partial {out_{h_1}}}+\frac{\partial {E_{o_2}}}{\partial {out_{h_1}}}$ ，
其中 $\frac{\partial {E_{o_1}}}{\partial {out_{h_1}}}=\frac{\partial {E_{o_1}}}{\partial {net_{o_1}}}\times \frac{\partial {net_{o_1}}}{\partial {out_{h_1}}}=\delta_{o_1}\times \frac{\partial {net_{o_1}}}{\partial {out_{h_1}}}=\delta_{o_1}\times \frac{\partial}{\partial {out_{h_1}}}(w_5\times out_{h_1}+w_6\times out_{h_2}+b_2\times 1)=\delta_{o_1}w_5$ ，這裡 $\delta_{o_1}$ 之前計算過。
$\frac{\partial {E_{o_2}}}{\partial {out_{h_1}}}$ 的計算也類似，所以得到
$\frac{\partial {E_{total}}}{\partial {out_{h_1}}}=\delta_{o_1}w_5+\delta_{o_2}w_7$ 。
$\frac{\partial {E_{total}}}{\partial {w_1}}$ 的鏈式中其他兩項如下：
$\frac{\partial {out_{h_1}}}{\partial {net_{h_1}}}=out_{h_1}(1-out_{h_1})$ ，
$\frac{\partial {net_{h_1}}}{\partial {w_1}}=\frac{\partial }{\partial {w_1}}(w_1\times i_1+w_2\times i_2+b_1\times 1)=i_1$
相乘得到
$\frac{\partial {E_{total}}}{\partial {w_1}}=\frac{\partial {E_{total}}}{\partial {out_{h_1}}}\frac{\partial {out_{h_1}}}{\partial {net_{h_1}}}\frac{\partial {net_{h_1}}}{\partial {w_1}}=(\delta_{o_1}w_5+\delta_{o_2}w_7)\times out_{h_1}(1-out_{h_1}) \times i_1$
得到梯度後，就可以對 $w_1$ 迭代了：
$w_1^+=w_1-\eta \frac{\partial{E_{total}}}{\partial{w_1}}$ 。

在前一個式子裡同樣可以對 $\delta_{h_1}$ 進行定義， $\delta_{h_1}=\frac{\partial {E_{total}}}{\partial {out_{h_1}}}\frac{\partial {out_{h_1}}}{\partial {net_{h_1}}}=(\delta_{o_1}w_5+\delta_{o_2}w_7)\times out_{h_1}(1-out_{h_1}) =(\sum_o \delta_ow_{ho})\times out_{h_1}(1-out_{h_1})$ ，所以整個梯度可以寫成 $\frac{\partial {E_{total}}}{\partial {w_1}}=\delta_{h_1}\times i_1$