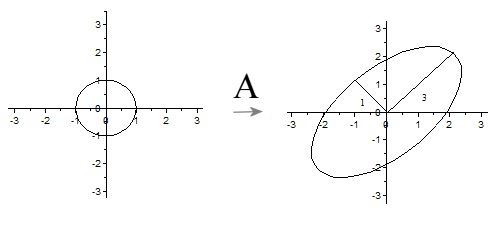奇異值分解的理解
阿新 • • 發佈:2019-01-10
我們都知道,圖片實際上對應著一個矩陣,矩陣的大小就是畫素大小,比如這張圖對應的矩陣階數就是450*333,矩陣上每個元素的數值對應著畫素值。我們記這個畫素矩陣為
現在我們對矩陣 進行奇異值分解。直觀上,奇異值分解將矩陣分解成若干個秩一矩陣之和,用公式表示就是:
進行奇異值分解。直觀上,奇異值分解將矩陣分解成若干個秩一矩陣之和,用公式表示就是:

其中等式右邊每一項前的係數 就是奇異值,
就是奇異值, 和
和 分別表示列向量,秩一矩陣的意思是矩陣秩為1。注意到每一項
分別表示列向量,秩一矩陣的意思是矩陣秩為1。注意到每一項 都是秩為1的矩陣。我們假定奇異值滿足
都是秩為1的矩陣。我們假定奇異值滿足 (奇異值大於0是個重要的性質,但這裡先別在意),如果不滿足的話重新排列順序即可,這無非是編號順序的問題。
(奇異值大於0是個重要的性質,但這裡先別在意),如果不滿足的話重新排列順序即可,這無非是編號順序的問題。
既然奇異值有從大到小排列的順序,我們自然要問,如果只保留大的奇異值,捨去較小的奇異值,這樣(1)式裡的等式自然不再成立,那會得到怎樣的矩陣——也就是影象?
令 ,這隻保留(1)中等式右邊第一項,然後作圖:
,這隻保留(1)中等式右邊第一項,然後作圖:
結果就是完全看不清是啥……我們試著多增加幾項進來: ,再作圖
,再作圖
隱約可以辨別這是短髮伽椰子的臉……但還是很模糊,畢竟我們只取了5個奇異值而已。下面我們取20個奇異值試試,也就是(1)式等式右邊取前20項構成
雖然還有些馬賽克般的模糊,但我們總算能辨別出這是Juri醬的臉。當我們取到(1)式等式右邊前50項時:
我們得到和原圖差別不大的影象。也就是說當 從1不斷增大時,
從1不斷增大時, 不斷的逼近
不斷的逼近 。讓我們回到公式
。讓我們回到公式

矩陣 表示一個450*333的矩陣,需要儲存
表示一個450*333的矩陣,需要儲存 個元素的值。等式右邊
個元素的值。等式右邊 和
和 分別是450*1和333*1的向量,每一項有
分別是450*1和333*1的向量,每一項有 個元素。如果我們要儲存很多高清的圖片,而又受限於儲存空間的限制,在儘可能保證影象可被識別的精度的前提下,我們可以保留奇異值較大的若干項,捨去奇異值較小的項即可。例如在上面的例子中,如果我們只保留奇異值分解的前50項,則需要儲存的元素為
個元素。如果我們要儲存很多高清的圖片,而又受限於儲存空間的限制,在儘可能保證影象可被識別的精度的前提下,我們可以保留奇異值較大的若干項,捨去奇異值較小的項即可。例如在上面的例子中,如果我們只保留奇異值分解的前50項,則需要儲存的元素為 ,和儲存原始矩陣
,和儲存原始矩陣 相比,儲存量僅為後者的26%。
相比,儲存量僅為後者的26%。
下面可以回答題主的問題:奇異值往往對應著矩陣中隱含的重要資訊,且重要性和奇異值大小正相關。每個矩陣
 的權重。
的權重。
在影象處理領域,奇異值不僅可以應用在資料壓縮上,還可以對影象去噪。如果一副影象包含噪聲,我們有理由相信那些較小的奇異值就是由於噪聲引起的。當我們強行令這些較小的奇異值為0時,就可以去除圖片中的噪聲。如下是一張25*15的影象(本例來源於[1])
但往往我們只能得到如下帶有噪聲的影象(和無噪聲影象相比,下圖的部分白格子中帶有灰色):
通過奇異值分解,我們發現矩陣的奇異值從大到小分別為:14.15,4.67,3.00,0.21,……,0.05。除了前3個奇異值較大以外,其餘奇異值相比之下都很小。強行令這些小奇異值為0,然後只用前3個奇異值構造新的矩陣,得到
奇異值分解還廣泛的用於主成分分析(Principle Component Analysis,簡稱PCA)和推薦系統(如Netflex的電影推薦系統)等。在這些應用領域,奇異值也有相應的意義。
考慮題主在問題描述中的敘述:“把m*n矩陣看作從m維空間到n維空間的一個線性對映,是否:各奇異向量就是座標軸,奇異值就是對應座標的係數?”我猜測,題主更想知道的是奇異值在數學上的幾何含義,而非應用中的物理意義。下面簡單介紹一下奇異值的幾何含義,主要參考文獻是美國數學協會網站上的文章[1]。
下面的討論需要一點點線性代數的知識。線性代數中最讓人印象深刻的一點是,要將矩陣和空間中的線性變換視為同樣的事物。比如對角矩陣 作用在任何一個向量上
作用在任何一個向量上

其幾何意義為在水平 方向上拉伸3倍,
方向上拉伸3倍, 方向保持不變的線性變換。換言之對角矩陣起到作用是將水平垂直網格作水平拉伸(或者反射後水平拉伸)的線性變換。
方向保持不變的線性變換。換言之對角矩陣起到作用是將水平垂直網格作水平拉伸(或者反射後水平拉伸)的線性變換。
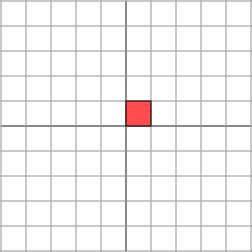
如果 不是對角矩陣,而是一個對稱矩陣
不是對角矩陣,而是一個對稱矩陣

那麼,我們也總可以找到一組網格線,使得矩陣作用在該網格上僅僅表現為(反射)拉伸變換,而沒有旋轉變換
考慮更一般的非對稱矩陣

很遺憾,此時我們再也找不到一組網格,使得矩陣作用在該網格上之後只有拉伸變換(找不到背後的數學原因是對一般非對稱矩陣無法保證在實數域上可對角化,不明白也不要在意)。我們退求其次,找一組網格,使得矩陣作用在該網格上之後允許有拉伸變換和旋轉變換,但要保證變換後的網格依舊互相垂直。這是可以做到的
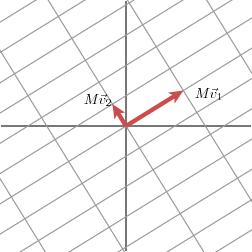
下面我們就可以自然過渡到奇異值分解的引入。奇異值分解的幾何含義為:對於任何的一個矩陣,我們要找到一組兩兩正交單位向量序列,使得矩陣作用在此向量序列上後得到新的向量序列保持兩兩正交。下面我們要說明的是,奇異值的幾何含義為:這組變換後的新的向量序列的長度。
當矩陣 作用在正交單位向量
作用在正交單位向量 和
和 上之後,得到
上之後,得到 和
和 也是正交的。令
也是正交的。令 和
和 分別是
分別是 和
和 方向上的單位向量,即
方向上的單位向量,即 ,
, ,寫在一起就是
,寫在一起就是![M\left[ v_1\quad v_2 \right]=\left[ \sigma_1u_1\quad \sigma_2u_2 \right]](https://zhihu.com/equation?tex=M%5Cleft%5B+v_1%5Cquad++v_2+%5Cright%5D%3D%5Cleft%5B+%5Csigma_1u_1%5Cquad++%5Csigma_2u_2+%5Cright%5D) ,整理得:
,整理得:
![M=M\left[ v_1\quad v_2 \right]\begin{bmatrix}v_1^{\rm T} \\v_2^{\rm T}\end{bmatrix}=\left[ \sigma_1u_1\quad \sigma_2u_2 \right]\begin{bmatrix}v_1^{\rm T} \\v_2^{\rm T}\end{bmatrix}=\left[ u_1\quad u_2 \right]\begin{bmatrix}\sigma_1 & 0 \\0 & \sigma_2\end{bmatrix}\begin{bmatrix}v_1^{\rm T} \\v_2^{\rm T}\end{bmatrix}](https://zhihu.com/equation?tex=M%3DM%5Cleft%5B+v_1%5Cquad++v_2+%5Cright%5D%0A%5Cbegin%7Bbmatrix%7D%0Av_1%5E%7B%5Crm+T%7D+%5C%5C%0Av_2%5E%7B%5Crm+T%7D%0A%5Cend%7Bbmatrix%7D%0A%3D%5Cleft%5B+%5Csigma_1u_1%5Cquad++%5Csigma_2u_2+%5Cright%5D%0A%5Cbegin%7Bbmatrix%7D%0Av_1%5E%7B%5Crm+T%7D+%5C%5C%0Av_2%5E%7B%5Crm+T%7D%0A%5Cend%7Bbmatrix%7D%0A%3D%5Cleft%5B+u_1%5Cquad++u_2+%5Cright%5D%0A%5Cbegin%7Bbmatrix%7D%0A%5Csigma_1+%26+0+%5C%5C%0A0+%26+%5Csigma_2%0A%5Cend%7Bbmatrix%7D%0A%5Cbegin%7Bbmatrix%7D%0Av_1%5E%7B%5Crm+T%7D+%5C%5C%0Av_2%5E%7B%5Crm+T%7D%0A%5Cend%7Bbmatrix%7D)
這樣就得到矩陣 的奇異值分解。奇異值
的奇異值分解。奇異值 和
和 分別是
分別是 和
和 的長度。很容易可以把結論推廣到一般
的長度。很容易可以把結論推廣到一般 維情形。
維情形。
下面給出一個更簡潔更直觀的奇異值的幾何意義(參見[2])。先來一段線性代數的推導,不想看也可以略過,直接看黑體字幾何意義部分:
假設矩陣 的奇異值分解為
的奇異值分解為
![A=\left[ u_1\quad u_2 \right]\begin{bmatrix}3 & 0 \\0 & 1\end{bmatrix}\begin{bmatrix}v_1^{\rm T} \\v_2^{\rm T}\end{bmatrix}](https://zhihu.com/equation?tex=A%3D%5Cleft%5B+u_1%5Cquad+u_2+%5Cright%5D%0A%5Cbegin%7Bbmatrix%7D%0A3+%26+0+%5C%5C%0A0+%26+1%0A%5Cend%7Bbmatrix%7D%0A%5Cbegin%7Bbmatrix%7D%0Av_1%5E%7B%5Crm+T%7D+%5C%5C%0Av_2%5E%7B%5Crm+T%7D%0A%5Cend%7Bbmatrix%7D)
其中 是二維平面的向量。根據奇異值分解的性質,
是二維平面的向量。根據奇異值分解的性質, 線性無關,
線性無關, 線性無關。那麼對二維平面上任意的向量
線性無關。那麼對二維平面上任意的向量 ,都可以表示為:
,都可以表示為: 。
。
當 作用在
作用在 上時,
上時,
![y=Ax=A[v_1\quad v_2]\begin{bmatrix}\xi_1 \\\xi_2\end{bmatrix}=\left[ u_1\quad u_2 \right]\begin{bmatrix}3 & 0 \\0 & 1\end{bmatrix}\begin{bmatrix}v_1^{\rm T} \\v_2^{\rm T}\end{bmatrix}[v_1\quad v_2]\begin{bmatrix}\xi_1 \\\xi_2\end{bmatrix}=3\xi_1u_1+\xi_2u_2](https://zhihu.com/equation?tex=y%3DAx%3DA%5Bv_1%5Cquad+v_2%5D%0A%5Cbegin%7Bbmatrix%7D%0A%5Cxi_1+%5C%5C%0A%5Cxi_2%0A%5Cend%7Bbmatrix%7D%3D%0A%5Cleft%5B+u_1%5Cquad+u_2+%5Cright%5D%0A%5Cbegin%7Bbmatrix%7D%0A3+%26+0+%5C%5C%0A0+%26+1%0A%5Cend%7Bbmatrix%7D%0A%5Cbegin%7Bbmatrix%7D%0Av_1%5E%7B%5Crm+T%7D+%5C%5C%0Av_2%5E%7B%5Crm+T%7D%0A%5Cend%7Bbmatrix%7D%0A%5Bv_1%5Cquad+v_2%5D%0A%5Cbegin%7Bbmatrix%7D%0A%5Cxi_1+%5C%5C%0A%5Cxi_2%0A%5Cend%7Bbmatrix%7D%3D3%5Cxi_1u_1%2B%5Cxi_2u_2)
令 ,我們可以得出結論:如果
,我們可以得出結論:如果 是在單位圓
是在單位圓 上,那麼
上,那麼 正好在橢圓
正好在橢圓 上。這表明:矩陣
上。這表明:矩陣 將二維平面中單位圓變換成橢圓,而兩個奇異值正好是橢圓的兩個半軸長,長軸所在的直線是
將二維平面中單位圓變換成橢圓,而兩個奇異值正好是橢圓的兩個半軸長,長軸所在的直線是 ,短軸所在的直線是
,短軸所在的直線是 .
.
推廣到一般情形:一般矩陣 將單位球
將單位球 變換為超橢球面
變換為超橢球面 ,那麼矩陣
,那麼矩陣 的每個奇異值恰好就是超橢球的每條半軸長度。
的每個奇異值恰好就是超橢球的每條半軸長度。
參考文獻:
[1] We Recommend a Singular Value Decomposition(Feature Column from the AMS)
[2] 徐樹方,《矩陣計算的理論與方法》,北京大學出版社。
現在我們對矩陣
其中等式右邊每一項前的係數
既然奇異值有從大到小排列的順序,我們自然要問,如果只保留大的奇異值,捨去較小的奇異值,這樣(1)式裡的等式自然不再成立,那會得到怎樣的矩陣——也就是影象?
令
結果就是完全看不清是啥……我們試著多增加幾項進來:
隱約可以辨別這是短髮伽椰子的臉……但還是很模糊,畢竟我們只取了5個奇異值而已。下面我們取20個奇異值試試,也就是(1)式等式右邊取前20項構成
雖然還有些馬賽克般的模糊,但我們總算能辨別出這是Juri醬的臉。當我們取到(1)式等式右邊前50項時:
我們得到和原圖差別不大的影象。也就是說當
矩陣
下面可以回答題主的問題:奇異值往往對應著矩陣中隱含的重要資訊,且重要性和奇異值大小正相關。每個矩陣
在影象處理領域,奇異值不僅可以應用在資料壓縮上,還可以對影象去噪。如果一副影象包含噪聲,我們有理由相信那些較小的奇異值就是由於噪聲引起的。當我們強行令這些較小的奇異值為0時,就可以去除圖片中的噪聲。如下是一張25*15的影象(本例來源於[1])
但往往我們只能得到如下帶有噪聲的影象(和無噪聲影象相比,下圖的部分白格子中帶有灰色):
通過奇異值分解,我們發現矩陣的奇異值從大到小分別為:14.15,4.67,3.00,0.21,……,0.05。除了前3個奇異值較大以外,其餘奇異值相比之下都很小。強行令這些小奇異值為0,然後只用前3個奇異值構造新的矩陣,得到
奇異值分解還廣泛的用於主成分分析(Principle Component Analysis,簡稱PCA)和推薦系統(如Netflex的電影推薦系統)等。在這些應用領域,奇異值也有相應的意義。
考慮題主在問題描述中的敘述:“把m*n矩陣看作從m維空間到n維空間的一個線性對映,是否:各奇異向量就是座標軸,奇異值就是對應座標的係數?”我猜測,題主更想知道的是奇異值在數學上的幾何含義,而非應用中的物理意義。下面簡單介紹一下奇異值的幾何含義,主要參考文獻是美國數學協會網站上的文章[1]。
下面的討論需要一點點線性代數的知識。線性代數中最讓人印象深刻的一點是,要將矩陣和空間中的線性變換視為同樣的事物。比如對角矩陣
其幾何意義為在水平
如果
那麼,我們也總可以找到一組網格線,使得矩陣作用在該網格上僅僅表現為(反射)拉伸變換,而沒有旋轉變換
考慮更一般的非對稱矩陣
很遺憾,此時我們再也找不到一組網格,使得矩陣作用在該網格上之後只有拉伸變換(找不到背後的數學原因是對一般非對稱矩陣無法保證在實數域上可對角化,不明白也不要在意)。我們退求其次,找一組網格,使得矩陣作用在該網格上之後允許有拉伸變換和旋轉變換,但要保證變換後的網格依舊互相垂直。這是可以做到的
下面我們就可以自然過渡到奇異值分解的引入。奇異值分解的幾何含義為:對於任何的一個矩陣,我們要找到一組兩兩正交單位向量序列,使得矩陣作用在此向量序列上後得到新的向量序列保持兩兩正交。下面我們要說明的是,奇異值的幾何含義為:這組變換後的新的向量序列的長度。
當矩陣
這樣就得到矩陣
下面給出一個更簡潔更直觀的奇異值的幾何意義(參見[2])。先來一段線性代數的推導,不想看也可以略過,直接看黑體字幾何意義部分:
假設矩陣
其中
當
令
推廣到一般情形:一般矩陣
參考文獻:
[1] We Recommend a Singular Value Decomposition(Feature Column from the AMS)
[2] 徐樹方,《矩陣計算的理論與方法》,北京大學出版社。

 結果就是完全看不清是啥……我們試著多增加幾項進來:
結果就是完全看不清是啥……我們試著多增加幾項進來: 隱約可以辨別這是短髮伽椰子的臉……但還是很模糊,畢竟我們只取了5個奇異值而已。下面我們取20個奇異值試試,也就是(1)式等式右邊取前20項構成
隱約可以辨別這是短髮伽椰子的臉……但還是很模糊,畢竟我們只取了5個奇異值而已。下面我們取20個奇異值試試,也就是(1)式等式右邊取前20項構成 雖然還有些馬賽克般的模糊,但我們總算能辨別出這是Juri醬的臉。當我們取到(1)式等式右邊前50項時:
雖然還有些馬賽克般的模糊,但我們總算能辨別出這是Juri醬的臉。當我們取到(1)式等式右邊前50項時: 我們得到和原圖差別不大的影象。也就是說當
我們得到和原圖差別不大的影象。也就是說當 但往往我們只能得到如下帶有噪聲的影象(和無噪聲影象相比,下圖的部分白格子中帶有灰色):
但往往我們只能得到如下帶有噪聲的影象(和無噪聲影象相比,下圖的部分白格子中帶有灰色): 通過奇異值分解,我們發現矩陣的奇異值從大到小分別為:14.15,4.67,3.00,0.21,……,0.05。除了前3個奇異值較大以外,其餘奇異值相比之下都很小。強行令這些小奇異值為0,然後只用前3個奇異值構造新的矩陣,得到
通過奇異值分解,我們發現矩陣的奇異值從大到小分別為:14.15,4.67,3.00,0.21,……,0.05。除了前3個奇異值較大以外,其餘奇異值相比之下都很小。強行令這些小奇異值為0,然後只用前3個奇異值構造新的矩陣,得到
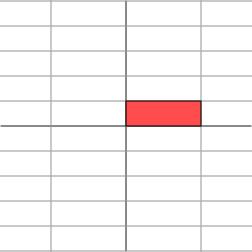 如果
如果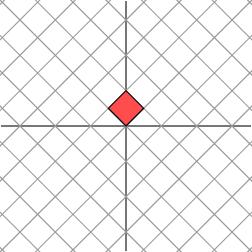
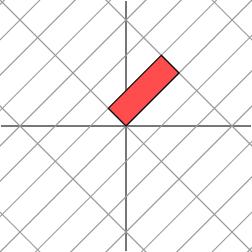 考慮更一般的非對稱矩陣
考慮更一般的非對稱矩陣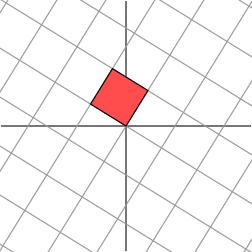
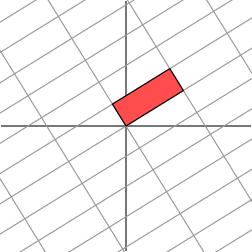 下面我們就可以自然過渡到奇異值分解的引入。奇異值分解的幾何含義為:對於任何的一個矩陣,我們要找到一組兩兩正交單位向量序列,使得矩陣作用在此向量序列上後得到新的向量序列保持兩兩正交。下面我們要說明的是,奇異值的幾何含義為:這組變換後的新的向量序列的長度。
下面我們就可以自然過渡到奇異值分解的引入。奇異值分解的幾何含義為:對於任何的一個矩陣,我們要找到一組兩兩正交單位向量序列,使得矩陣作用在此向量序列上後得到新的向量序列保持兩兩正交。下面我們要說明的是,奇異值的幾何含義為:這組變換後的新的向量序列的長度。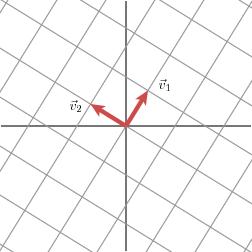
 當矩陣
當矩陣