邏輯迴歸模型的兩種定義與引數估計思路
邏輯斯諦迴歸(logistic regression)是統計學習中的經典分類方法,屬於判別模型。
1. 邏輯斯諦迴歸模型定義
在 Andrew NG 的 Machine Learning 課程和李航的統計學習方法中,都有對邏輯斯諦迴歸模型的介紹,然而二者卻對模型有著不同的定義。
1.1 決策函式
Andrew NG 課程中,對二項邏輯迴歸模型的決策函式如下:
其中
1.2 條件概率分佈
統計學習方法中,二項邏輯迴歸模型是如下函式定義的條件概率分佈:
這裡,
2. 模型引數估計
由於定義的模型存在差異,因此二者的引數估計的思路也不同。
2.1 誤差之和極小化
Andrew NG 課程中對誤差之和的計算方法如下:
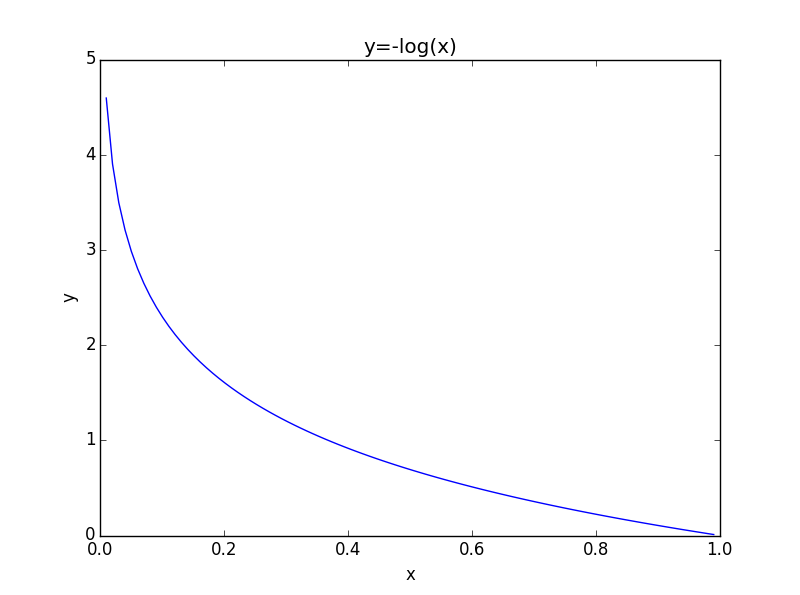
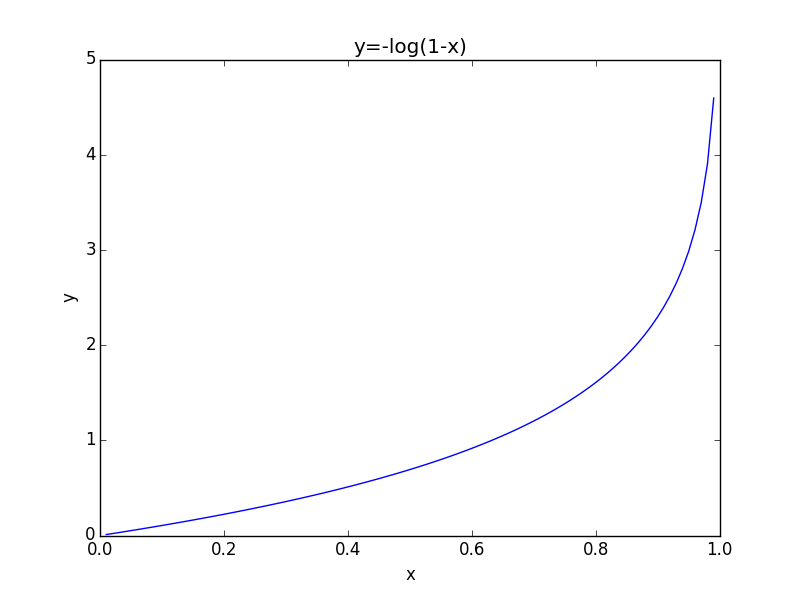
Cost函式可統一成以下形式:
最終的誤差函式如下:
求解誤差函式的極小值,即可得到
邏輯斯諦迴歸(logistic regression)是統計學習中的經典分類方法,屬於判別模型。
1. 邏輯斯諦迴歸模型定義
在 Andrew NG 的 Machine Learning 課程和李航的統計學習方法中,都有對邏輯斯諦迴歸模型的介紹,然而二者
邏輯迴歸(Logistic Regression, LR)是傳統機器學習中的一種分類模型,由於演算法的簡單和高效,在實際中應用非常廣泛。它的起源非常複雜,可以看參考引用1。具體應用實踐可以看這裡。
問題背景
對於二元分類問題,給定一個輸入特徵向量XX(例 命名 c++ ech += esp set with aced spa 類內定義
class Teacher
{
private:
string _name;
int _age;
public:
Teacher()
{
printf("create teche alt obj tro tran padding pad hit object 方式 裝飾器方式:[email protected]/* */
經典類,[email protected]/* */(如上一步實例)
# ############### 重復 及其 orf with gpo val 定義 系統 brush
# tensorflow中的兩種定義scope(命名變量)的方式tf.get_variable和tf.Variable。Tensorflow當中有兩種途徑生成變量 variable
import te cti 函數名 arguments ros 表達 length 16px 列表 microsoft 1.聲明式函數:function test(){};
2.表達式函數:var test=function(){}
例:function test(a,b){}
test( linux 運維 系統 擴容 磁盤 /dev/mapper/VolGroup-lv_root是一個邏輯卷,通過df –h命令你可以發現它與“/”根分區相關聯,你也可以理解為它就是根分區。
[root@localhost ~]# df -h
Filesystem Siz 建立程序的兩種方式
第一種使用multprocessing 開啟子程序第二種使用自定義的方式(設計繼承程序類的方式)
from multiprocessing import Process
class MyProcess(Process):
def run(self):
p # class Foo(object):# def __init__(self, name):# self.name = name### f = Foo("alex")# print(type(f))# print(type(Foo))def func(self): print(
問題:
執行模型輸出loss值為NAN,訓練200次後未出現線性模型
nan
nan的資料型別為float, not a number 的縮寫。python中判斷是否為nan型別的方法,使用math庫中的*isnan()*函式判斷:
from math import
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import input_data
mnist = input_data.read_data_sets('data/', one_hot=True)
本案例主要是通過對不均衡的28萬組資料建立模型,分析預測欺詐使用者,採用sigmod函式作為損失函式,採用交叉驗證的方法
和l1正交法則,比對了不同懲罰函式下的模型的召回率,也通過預測值和實際值做出混淆矩陣更加直觀看到各種預測結果。
也比較了sigmod函式下的不同閾值下的模型預測的精度和召
在日常學習或工作中經常會使用線性迴歸模型對某一事物進行預測,例如預測房價、身高、GDP、學生成績等,發現這些被預測的變數都屬於連續型變數。然而有些情況下,被預測變數可能是二元變數,即成功或失敗、流失或不流失、漲或跌等,對於這類問題,線性迴歸將束手無策。這個時候就需要另一種
符號常量 #define Pi 3.1415926f;
常值變數 const float pi 3.1415926f;
第一種方式:巨集定義,是將Pi定義成一種符號,此時Pi只是3.1415926的別名,在編譯期間用3.1415926去取代Pi的值。
1.define是巨集定義,程式在預處
邏輯迴歸被廣泛的用來解決分類問題。由於分類是非線性問題,所以建模的主要難點是如何把非線性問題轉換為線性問題。
在模型評估層面,討論了兩類相互有關聯的評估指標。對於分類問題的預測結果,可以定義為相應的查準查全率。對於基於概率的分類模型,還可以繪製它的ROC曲線,以及計算曲線線面的面積AUC。
任務
預測貸款客戶是否會逾期,status為響應變數,有0和1兩種值,0表示未逾期,1表示逾期。
程式碼:
# -*- coding: utf-8 -*- """ Created on Thu Nov 15 13:02:11 2018
關於JAVA中兩種字串定義方式的區別
第一次寫,就當複習總結一下,希望能幫到需要的人吧= =
我們知道在JAVA中,對於字串的例項化方式有兩種:
直接賦值:String str = “Hello World”;
構造方法例項化:String str = new
本篇不講演算法
只講用Python (pandas, matplotlib, numpy, sklearn) 進行訓練的一些要點
1.合併index
np.concatenate([index1,index2])
2.from sklearn.cross_va
任務
預測貸款使用者是否會逾期,status為響應變數,有0和1兩種值。
程式碼:
# -*- coding: utf-8 -*-
"""
Created on Thu Nov 15 13:02:11 2018
@author: keepi
"""
i
離散化是什麼:一些數字,他們的範圍很大(0-1e9),但是個數不算多(1-1e5),並且這些數本身的數字大小不重要,重要的是這些數字之間的相對大小(比如說某個數字是這些數字中的第幾小,而與這個數字本身大小沒有關係,要的是相對大小)(6 8 9 4 離散化後即為 2 3 4 1 相關推薦
邏輯迴歸模型的兩種定義與引數估計思路
LR(Logistic Regression) 邏輯迴歸模型 進行二分類或多分類 及梯度下降學習引數
C++ 類的兩種定義方式
屬性的兩種定義方式
TF之RNN:TF的RNN中的常用的兩種定義scope的方式get_variable和Variable—Jason niu
js函數的兩種定義形式,函數的實參列表arguments/形參列表函數名
/dev/mapper/VolGroup-lv_root爆滿兩種可能與及根分區擴容
建立的程序的兩種方式與常用屬性
類的兩種定義
清華AI自強計劃作業2實驗—邏輯迴歸模型
tensorflow構造邏輯迴歸模型
實戰:利用Python sklearn庫裡的邏輯迴歸模型訓練資料---建立模型
邏輯迴歸模型在R中實踐
常量的兩種定義方式比較
邏輯迴歸模型總結-機器學習
客戶貸款逾期預測[1]-邏輯迴歸模型
JAVA字串的兩種定義方式的區別
機器學習(四)邏輯迴歸模型訓練
邏輯迴歸模型實踐-貸款逾期預測
離散化的思想和它的兩種程式碼與區別
