常見經典排序演算法有：氣泡排序，快速排序，插入排序，選擇排序，歸併排序、希爾排序。
氣泡排序就不介紹了，首先是快速排序QuickSort：
過一趟排序將要排序的資料分割成獨立的兩部分，其中一部分的所有資料都比另外一部分的所有資料都要小，然後再按此方法對這兩部分資料分別進行快速排序，整個排序過程可以遞迴進行，以此達到整個資料變成有序序列。

如資料為  6   2   7  3  8  9
first：
furst -1
first -a:3 2 7 6 8 9(從後往前，找比6（第一個資料）小的數交換）
first -b:3 2 6 7 8 9（再從前往後（從2開始），找比6大的資料
first
 
...一次按first-1來先找比6小，再找比6大，直至結束。
first-result：3 2 6 7 8 9
second:
以 6為界限，劃分兩部分 得 3 2與    7 8 9
先計算 3 2參照first;
再 7 8 9，同樣操作。

插入即表示將一個新的資料插入到一個有序陣列中，並繼續保持有序。

從第二個數字開始，假設前面的已經排好序，該數為帶插入前面有序的數字中，接著第三個，插入到前面序列
好了，快排就是這樣的，下面是插入排序

50，60,71,49,11,24,3,66  k=60(2)

50,60，71,49，11,24,66
next 插入
k=71(3)
50,60，71,49
 
,11,24,3,66）
k=49(4)（下一個）
50,60,49,71,11,24,3,69
50,49,60,71,..
49,50,60,71,11,24,3
k=11(第五個數）
...
...

選擇排序

每次找出最小數，從i=1 to n
example 3（start) 5 1 2 7 6
i=0,從j=1 to n找最小到第一個交換
1 5(start)  3 2 7 6
1 2 3 5 7 6
....

希爾排序

```
           9 1 2 5 7 4 8 6 3 6
first組合： 9         4 （比較交換）
             1         8
               2         6
                 5         3
                   7         6
組合（9[index1]
 
 4[index[5]），（1[2],8[6]）,(2[3],6[7]),...
排好序列歸位：
           4 1 2 3 6 9 8 6 5 7
再組合：    4   2   6   8   5
             1   3   9   6   7
             排序歸位
             ...            

           that's all!

歸併排序，簡單來說就是分治法，分治法被廣泛用於大資料，雲端計算中，比如hadoop的mapreduce很大一部分來源於此。14年本人看的第一篇論文就是並行歸併排序演算法，附上理解
Title：Parallel Merge Sort with Load Balancing
作者：Minsoo Jeon and Dongseung Kim
傳統的並行歸併排序介紹：
分解：將原問題分解成一系列子問題
解決：遞迴的解決各子問題
合併：將子問題的解合併成原問題的解
演算法思想：
1.將N個數據（平）分給P個處理器
2.P個處理器對每一組資料進行排序
3.把每兩個處理器排好的序列合併再排序，此時處於工作狀態的處理器數量減半
4.重複第3步，直到只剩下最後一個處理器處理所有資料，排序完畢。

begin
h :=P
1. forall 0 [ i [ P−1
     Pi sorts a list of N/P keys locally.
2. for j=0 to (log P)−1 do
        forall 0 [ i [ h−1
           if (i < h/2) then
              2.1. Pi receives N/h keys from Pi+h/2
              2.2. Pi merges two lists of N/h keys into a sorted list of 2N/h
          else
          2.3. Pi sends its list to Pi−h/2
      h :=h/2
end

/*
P：處理器數量
Pi:第i個處理器
h:處於工作狀態的處理器數量

*/

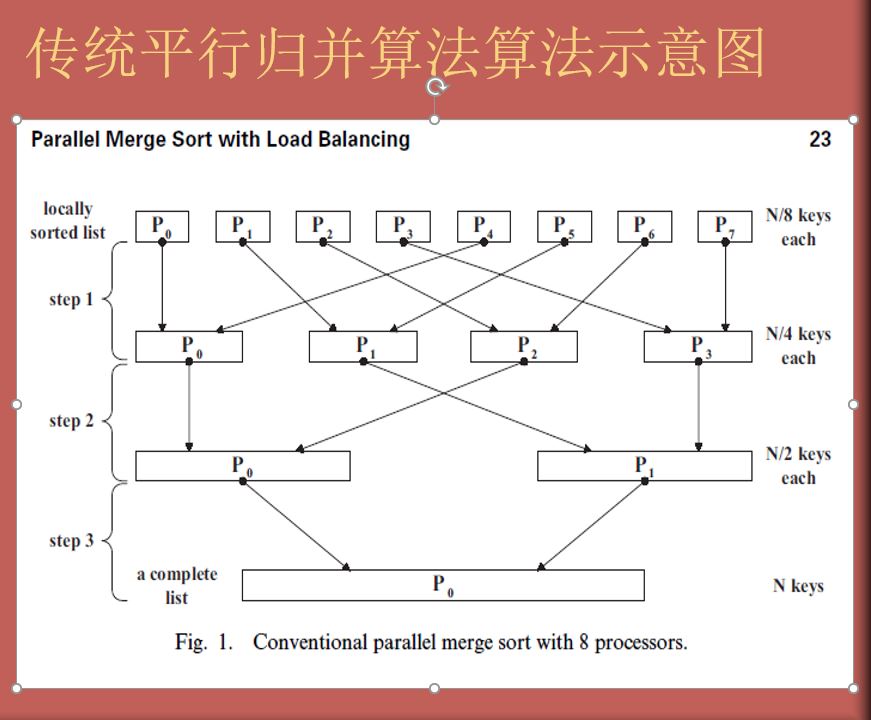
傳統平行歸併演算法演算法示意圖:

for example:

原始資料：14，1，18，2，16，4，7，21
STEP1：分給兩個處理器P0和P1：
P0：14，1，18，2                             P1：16，4，7，21
     Step2：P0和P1對兩組資料做快速排序：
P0：1, 2, 14,   18                               P1：4,7,16,21
     Step3:將P0裡的最小數與P1的最小數比較，P0裡1比P1裡的4小，然後進行下一步，繼續將P0的第二個數與P1的4比較，將P1的最小數在P0裡做插入排序，P1插入到P0的2和14之間，此時有：
 P0：1,2,4,14,18                               P1：7,16,21
     Step4:將P1的7從P0的4往後插入排序，以此遞迴，最後
    P0：1，2，4，7，14，16，18，21
   排序完畢，P1為空。      

code:

/*p[i]為第i塊處理器，建議開啟多執行緒模仿或者多處理器程式設計，本人只是做了實現，程式碼提供參考*/
#include<stdlib.h>
void sort1(int n,int a[])
{int i,j,key;
for(i=0;i<n;i++)
 for(j=i+1;j<n;j++)
    if(a[i]>a[j])
    { key=a[i];
      a[i]=a[j];
      a[j]=key;
    }
}
void sort2(int m,int a[],int b[])
{int i,j=0,k,s=m;
a[4]=65535;
b[4]=65535;
for(i=0;i<m;i++)
{ while(b[i]>a[j])
 {
 j++;
 }
 {{s++;
     for(k=s-1;k>j;k--)
         a[k]=a[k-1];

 }
 a[j]=b[i];}

}
}
void main()
{
int p[8];
int p0[8];
int p1[8];
int i;
printf("please input 8 keys:\n");
for(i=0;i<8;i++)
scanf("%d",&p[i]);
for(i=0;i<4;i++)
{p0[i]=p[i];
p1[i]=p[i+4];}
sort1(4,p0);
sort1(4,p1);
printf("\ndata in P0:\n");
for(i=0;i<4;i++)
printf("%d ",p0[i]);
printf("\ndata in P1:\n");
for(i=0;i<4;i++)
printf("%d ",p1[i]);
sort2(5,p0,p1);
printf("\nthe data sorted stores in P0:\n");
for(i=0;i<8;i++)
printf("%d ",p0[i]);

}

 平行歸併演算法在處理大量資料是非常有效，但是傳統的歸併演算法（分治法）效能很差，因為每次合併處理時，處理器就會減少一半，加重了每個處理器所處理的資料長度，合併到最後時，只有一個處理器處理所有的資料。
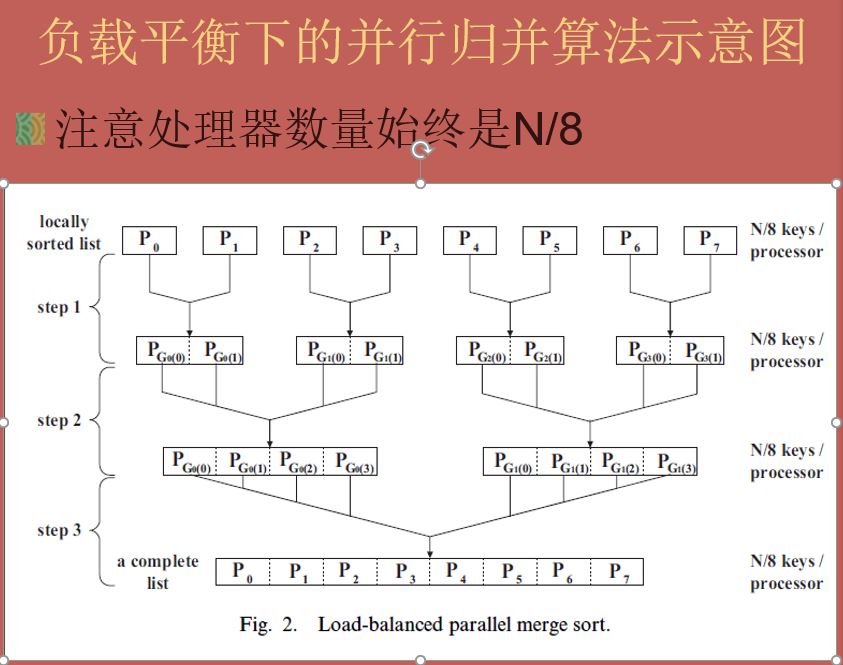
 相比其他快速法而言，它有利於處理大量資料，但是該傳統演算法越往後進行，就有越來越多的處理器處於閒置狀態，因此歸併排序演算法必須平行化處理，才能發揮出最大優勢，本文推薦了一種負載平衡下的並行歸併排序演算法，該演算法在整個計算過程中，所有處理器均參與計算。在每一個階段都分配資料到每一個處理器上。這樣效能就大大提高。

*下面就是介紹我們強大的負載平衡下的平行歸併演算法~~
演算法思想：
1.將N個帶排序資料（平）分給P個處理器；
2.P個處理器同時對P組資料進行排序（從小到大）；
3.將每兩個相鄰處理器做比較，將第一個處理器的最大數（最右邊數）與第二個處理器的最小數（最左邊數）作比較，若第一個處理器的最大數小於第二個處理器的最小數，則這兩個處理器的資料排序完成，反之，則交換邊界數，兩處理器又再次重新排序；
4.依次做遞迴，直到這兩組資料完全排序完成；
5.這時P個處理器在使用，待排序陣列變成P/2個數組；
6.依次遞迴進行歸併，把待排序陣列歸併，處理器並行適應，每次待排序陣列減半，直到結束為止。*

輸入原始資料：15,6,56,78,1,3,99,2
Step1:將資料平分給P0，P1
P0:15,6,56,78                P1:1,3,99,2
Step2:P0,P1兩組處理器分別對兩組數排序，拍完後：
P0:6,15,56,78                P1:1,2,3,99
Step3:比較P0中最右邊數（最大數）與P1最左邊數（最小數），若P0最大數小於P1最小數，則排序完成，反之，交換兩邊界數
Step4：交換後
P0：6，15，56,1         P1：78,2,3,99
Step5：重複Step2,Step3,Step4,直到結束，得到
P0：1,2，3，6             P1：15，56，78，99
排序完畢，P0中數小於P1中數

Here is the code:

#include<stdlib.h>
void sort1(int n,int a[])
{int i,j,key;
for(i=0;i<n;i++)
 for(j=i+1;j<n;j++)
    if(a[i]>a[j])
    { key=a[i];
      a[i]=a[j];
      a[j]=key;
    }
}
void main()
{
int p[8];
int p0[4];
int p1[4];
int i,data1;
printf("please input 8 keys:\n");
for(i=0;i<8;i++)
scanf("%d",&p[i]);
for(i=0;i<4;i++)
{p0[i]=p[i];
p1[i]=p[i+4];}
sort1(4,p0);
sort1(4,p1);
printf("data in P0:\n");
for(i=0;i<4;i++)
printf("%d ",p0[i]);
printf("\ndata in P1:\n");
for(i=0;i<4;i++)
printf("%d ",p1[i]);
while(p0[3]>p1[0]){
   data1=p0[3];
   p0[3]=p1[0];
   p1[0]=data1;
   printf("\ndata in P0:\n");
for(i=0;i<4;i++)
printf("%d ",p0[i]);
printf("\ndata in P1:\n");
for(i=0;i<4;i++)
printf("%d ",p1[i]);
sort1(4,p0);
sort1(4,p1);
 printf("\ndata in P0:\n");
for(i=0;i<4;i++)
printf("%d ",p0[i]);
printf("\ndata in P1:\n");
for(i=0;i<4;i++)
printf("%d ",p1[i]);


}
printf("\nthe data sorted stores in P0:\n");
for(i=0;i<4;i++)
printf("%d ",p0[i]);
printf("\nthe data sorted stores in P1:\n");
for(i=0;i<4;i++)
printf("%d ",p1[i]);

}
/*p[i]同樣是模擬第i塊處理器

*/

for example:

輸入原始資料：15,6,56,78,1,3,99,2
Step1:將資料平分給P0，P1
P0:15,6,56,78                P1:1,3,99,2
Step2:P0,P1兩組處理器分別對兩組數排序，拍完後：
P0:6,15,56,78                P1:1,2,3,99
Step3:比較P0中最右邊數（最大數）與P1最左邊數（最小數），若P0最大數小於P1最小數，則排序完成，反之，交換兩邊界數
Step4：交換後
P0：6，15，56,1         P1：78,2,3,99
Step5：重複Step2,Step3,Step4,直到結束，得到
P0：1,2，3，6             P1：15，56，78，99
排序完畢，P0中數小於P1中數

該演算法經常用於分散式檔案系統‘大資料處理，並行高效能運算。