之前在文章《<模型彙總_1>牛逼的深度卷積神經網路CNN》詳細介紹了卷積神經網路的基本原理，以及常見的基本模型，如LeNet，VGGNet，AlexNet，ReseNet，Inception Net的基本結構和原理。今天主要總結一下，卷積神經網路家族中，不同型別的卷積方式以及它們各自的優點。為了簡單起見，我們僅從2維的角度介紹。

文末提供相關資料下載地址

卷積基本概念

首先，我們首先回顧一下卷積相關的基本概念，定義一個卷積層需要的幾個引數。

2維卷積使用卷積核大小為3，步長為1和Padding

卷積核大小（Kernel Size）：卷積核大小定義了卷積的視野。2維中的常見選擇是3 - 即3x3畫素矩陣。

步長（Stride）：步長定義遍歷影象時卷積核的移動的步長。雖然它的預設值通常為1，但我們可以使用值為2的步長來對類似於MaxPooling的影象進行下采樣。

填充（Padding）：填充定義如何處理樣本的邊界。Padding的目的是保持卷積操作的輸出尺寸等於輸入尺寸，因為如果卷積核大於1，則不加Padding會導致卷積操作的輸出尺寸小於輸入尺寸。

輸入和輸出通道（Channels）：卷積層通常需要一定數量的輸入通道（I），並計算一定數量的輸出通道（O）。可以通過I * O * K來計算所需的引數，其中K等於卷積核中引數的數量，即卷積核大小。

下面介紹幾種常見的卷積方式。

擴張卷積（Dilated Convolution）

（又稱Atrous Convolution）

2維卷積，卷積核大小為3，擴張率（dilation rate）為2，無Padding

擴張卷積在進行卷積操作時引入了另一個引數，即擴張率，用以捕捉畫素之間的long dependency。擴張率定義了卷積核中的值與值之間的間隔。擴張率為2的3x3卷積核將具有與與5x5卷積核相同的視野，而只使用9個引數。想象一下，使用一個5x5卷積核並刪除第二行和列。

這樣操作，使得在相同的計算成本下，卷積計算具有更寬的視野，可以捕捉更長的依賴關係。擴張卷積在實時影象分割領域特別受歡迎。適用於需要更加寬泛的視野並且不用多個卷積或更大的卷積核情況。

可變形（Deformable）卷積

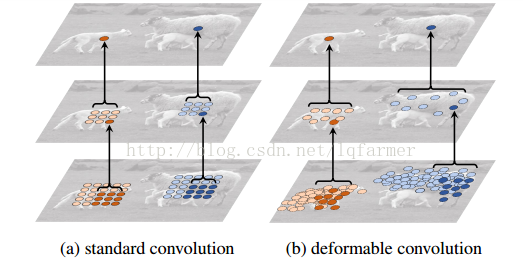
我們常見的卷積核（filter）一般都是呈長方形或正方形的，規則的卷積核往往會限制特徵抽取的有效性，更為有效的做法是讓卷積和具有任意的形狀，那麼卷積核是否可以呈圓形或者隨意的形狀呢？答案是可行的，如下圖所示，典型的代表就是Deformable Convolution Network。

對比上圖所示的a、b兩圖可以發現，任意形狀的的卷積核使得網路可以重點關注一些重要的區域，更能有效且準確的抽取輸入影象的特徵。

怎麼樣來實現呢？

如上圖所示，網路會根據原始的卷積，如圖a所示，學習一個offset偏量，通過一些列的旋轉、尺度變換、縮放等Transform變換，改變成成任意形狀的卷積核，如b、c、d圖所示。

Offet代表的Transform怎麼實現呢？

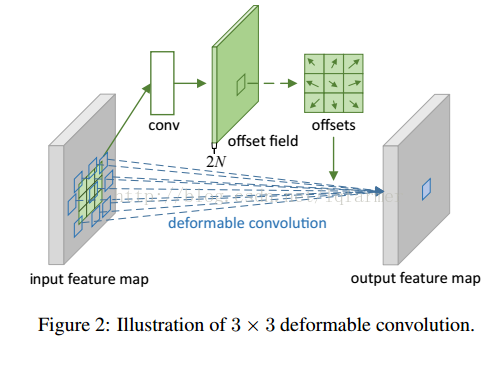
在deformable convolution中，會進行兩次卷積，第一次卷積計算得到offset的卷積核，第二次是利用第一步得到的offset卷積核進行常規的卷積得到最終輸出。重點是第一步中獲得offset卷積核。先從input feature map中通過卷積（conv）計算得到offset field，在基於offset field得到最終的offset。注意，offset得到的輸出通道數是input feature map的兩倍，因為offset包含了在x和y兩個方向上的偏置項。

深度可分離（Depth Separable）卷積

在可分離的卷積中，我們可以將卷積核操作拆分成多個步驟。我們用y = conv（x，k）表示卷積，其中y是輸出影象，x是輸入影象，k是卷積核。接下來，假設k由公式：k = k1.dot（k2）計算。這就是一個可分離的卷積，因為我們可以使用大小分別為k1和k2兩個卷積核進行2個1D卷積來取得相同的結果，而不是用一個大小k進行二維卷積。

Sobel X和Y卷積核

以Sobel卷積核為例，通常用於影象處理。我們可以通過向量[1，0，-1]乘以向量[1,2,1] 來獲得相同的卷積核。執行相同的操作，只需要6而不是9個引數。

上面的例子就是所謂的空間可分離卷積，但在深度學習中並不是這樣做的。這樣介紹主要是舉個例子，不至於使人迷惑。在神經網路中，通常使用稱為深度可分離卷積的網路，典型的網路Xception Net，示意圖如下圖所示。

深度可分離卷積在執行空間卷積的同時，保持通道（Channels）之間分離，然後按照深度方向（depth）進行卷積。用一個例子來說明。

假設在16個輸入通道和32個輸出通道上，採用3x3卷積核進行卷積計算，16個通道上採用3x3卷積核，進行32次重複操作，產生512（16x32）個特徵圖（feature map）。然後，把這些特徵圖合併得到一個輸出通道。重複執行32次，最終得到了32個輸出通道。

對於同一個例子，採用深度可分離方式進行卷積，採用3x3卷積核分別遍歷16個通道，最終得到16個特徵圖。現在，在進行合併操作之前，先採用32個1x1卷積個來遍歷這16個特徵圖，然後再把它們合併到一起。採用可分離卷積，有656（16x3x3 + 16x32x1x1）引數，相反，傳統卷積操作有4608（16x32x3x3）引數，大大減少了引數的數目。

該例子是一個典型的深度可分離卷積的例子，其中採用的深度乘數（Depth Multiplier）為1，也是一種最常見的設定。

這樣做是基於一個假設，即平面和深度方向資訊可以解耦。Xception網路證明了這個假設是有效的。因為可以有效地使用模型的引數，所以深度可分離的卷積可以用於可移動裝置上。

Squeeze-and-Excitation Convolution

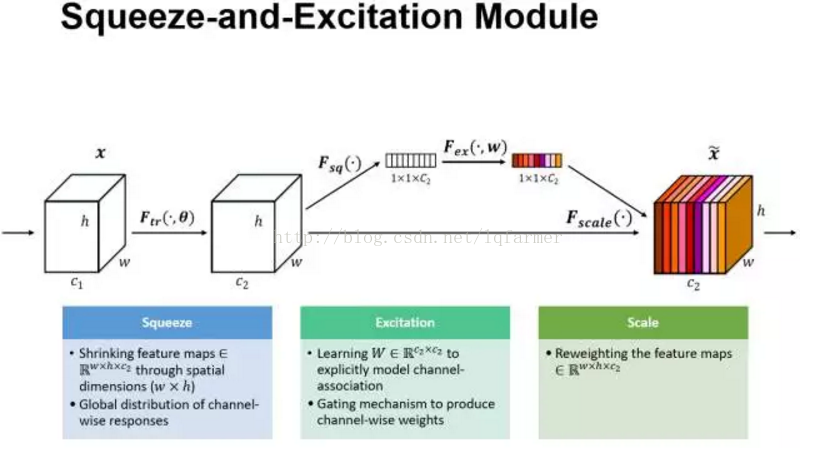
Squeeze-and-Excitation 來源於ImageNet2017年的冠軍網路SEnet。在傳統的LeNet、Inception、ReseNet、DenseNet中，我們認為所有的特徵通道（Channel）都是同等重要的，那是否可以給每個通道賦予一個權重呢？SEnet就通過Squeeze-and-Excitation block來實現了這一想法，當然CNN的網路結構十分靈活，還有很多其他簡單的實現方式，這裡就不一一列舉。Squeeze-and-Excitation block（簡稱SES 模組）如下圖所示。

以圖中為例，輸入X具有C1數目的通道，經過一系列變換得到通道數為C2的SES模組的輸入。資料進入SES模組分成兩路，如圖中，上面一路進行squeeze-excitation，Scale操作，下面一路進行傳統的卷積操作。在上面一路中，首先是Squeeze操作，沿著通道C2方向，採用Global Average pooling操作，把尺寸c2 X h X W的輸入pooling成一個c2 X 1 X 1的輸出，即把每一個二維的特徵圖轉換成一維的實數。Global Average pooling相當於一個全域性的感受野，可以獲取h X W整張圖片資訊，對應的標量輸出可以代表整張圖全域性分佈。然後進行Excitation操作，借鑑RNN中的Gate機制，為每一個通道賦予一個可訓練的權重W，通過W的學習，來建模通道間的重要性。最後是一個Sacle操作，通過Reweight操作把學習的到權重得到傳統的卷積得到的通道輸出上，得到通道的輸出特徵的重標定操作。

轉置（Transposed）卷積

（也稱為deconvolutions 或 fractionally stride卷積）

有些場景下使用deconvolution，這中說法其實不太合適，因為它不是一個deconvolution，真正的deconvolution應該是卷積操作的逆過程。雖然deconvolution確實存在，但它們在深度學習領域並不常見。想象一下，將影象輸入到單個卷積層。現在獲得輸出，把輸出扔到一個黑盒子裡，再恢復成的原始輸入影象。這個黑盒子才叫做deconvolution。Deconvolution是卷積計算過程的逆計算過程。

轉置卷積則比較貼切，因為轉置會產生相同的空間解析度。然而，真實執行的數學運算則稍有不同的。轉置卷積層一方面會執行常規卷積，同時也會恢復其空間變換。

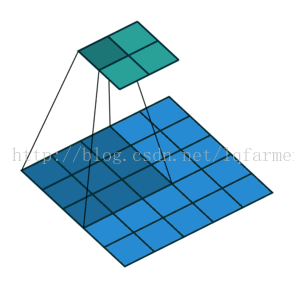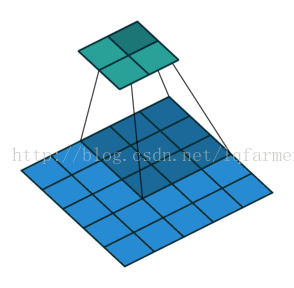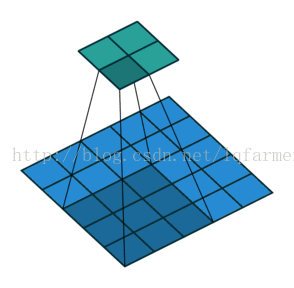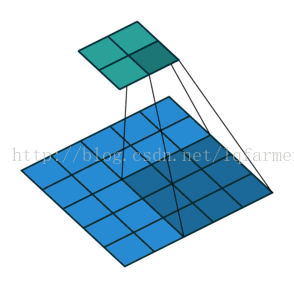
2維卷積無填充，步長為2和卷積核為3

這一點可能會讓人覺得有點難以理解，所以我們來看一個具體的例子，如上圖。5x5的影象被送入一個卷積層進行卷及計算。步長設定為2，沒有填充，卷積核為3x3。輸出為一個2x2影象。

如果我們想反轉這個過程，我們需要進行數學逆運算，這樣每一個輸入的畫素會產生9個輸出值。之後，我們以步長為2的速度遍歷輸出影象。這將是一個deconvolution操作，如下圖所示。

沒有填充的2維卷積，步長為2和卷積核為3

轉置卷積並不是這樣做的。與上述操作相比，唯一的共同之處在於，它保證輸出也將是5x5影象，同時仍然執行正常的卷積運算。為了實現這一點，我們需要在輸入影象上進行一些漂亮的填充。

你可以想象，這一步不會重複上面的過程。至少，數值上不會。它只是通過一個卷積操作來重構卷積操作的輸入。這並不是數學上的逆操作，只是一種Encoder-Decoder架構，但仍然非常有用。通過這種方式，我們可以通過一個卷積來放大一張圖片，而不需要進行兩個單獨的操作。

文中介紹的模型相關論文下載地址：

密碼: 公眾號回覆“cov”

往期精彩內容推薦：

更多深度學習在NLP方面應用的經典論文、實踐經驗和最新訊息，歡迎關注微信公眾號“深度學習與NLP”或“DeepLearning_NLP”或掃描二維碼新增關注。