前言

在介紹卷積神經網路中的1x1卷積之前，首先回顧卷積網路的基本概念[1]。

1. 卷積核（convolutional kernel）：可以看作對某個區域性的加權求和；它是對應區域性感知，它的原理是在觀察某個物體時我們既不能觀察每個畫素也不能一次觀察整體，而是先從區域性開始認識，這就對應了卷積。

   卷積核的大小一般有1x1,3x3和5x5的尺寸（一般是奇數x奇數）。卷積核的個數就對應輸出的通道數（channels），這裡需要說明的是對於輸入的每個通道，輸出每個通道上的卷積核是不一樣的。比如輸入是28x28x192(WxDxK,K代表通道數)，然後在3x3的卷積核，卷積通道數為128，那麼卷積的引數有3x3x192x128，其中前兩個對應的每個卷積裡面的引數，後兩個對應的卷積總的個數（一般理解為，卷積核的權值共享只在每個單獨通道上有效，至於通道與通道間的對應的卷積核是獨立不共享的，所以這裡是192x128）。

2. 池化（pooling）：卷積特徵往往對應某個區域性的特徵。要得到global的特徵需要將全域性的特徵執行一個aggregation（聚合）。

   池化就是這樣一個操作，對於每個卷積通道，將更大尺寸（甚至是global）上的卷積特徵進行pooling就可以得到更有全域性性的特徵。這裡的pooling當然就對應了cross region。與1x1的卷積相對應，而1x1卷積可以看作一個cross channel的pooling操作。pooling的另外一個作用就是升維或者降維，後面我們可以看到1x1的卷積也有相似的作用。

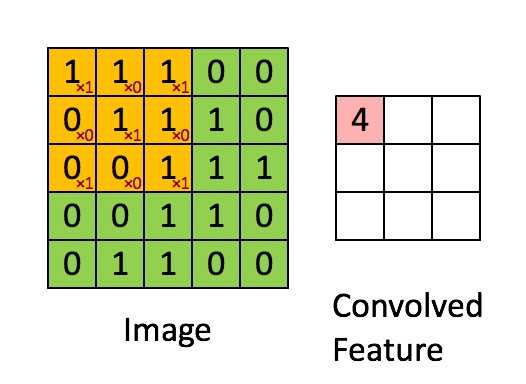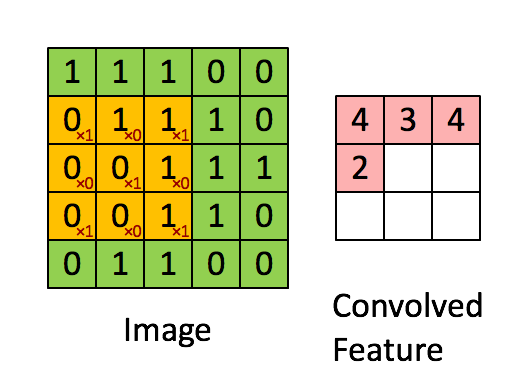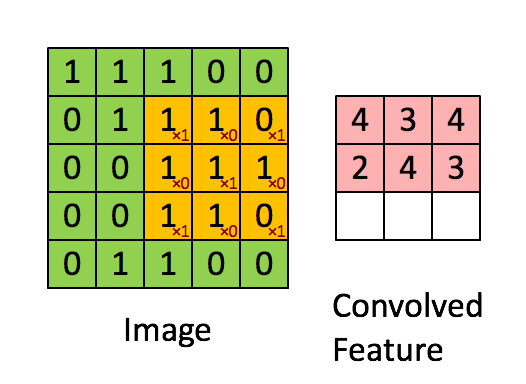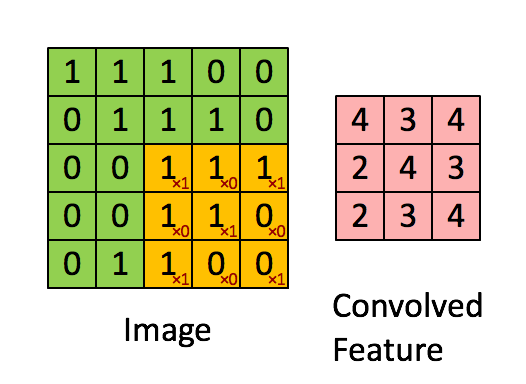
下面從一般卷積過程介紹1x1的卷積，下面動圖來表示卷積的過程：

1x1卷積核

1x1卷積，又稱為網中網（Network in Network）[2]。

這裡通過一個例子來直觀地介紹1x1卷積。輸入6x6x1的矩陣，這裡的1x1卷積形式為1x1x1，即為元素2，輸出也是6x6x1的矩陣。但輸出矩陣中的每個元素值是輸入矩陣中每個元素值x2的結果。

上述情況，並沒有顯示1x1卷積的特殊之處，那是因為上面輸入的矩陣channel為1，所以1x1卷積的channel也為1。這時候只能起到升維的作用。這並不是1x1卷積的魅力所在。

讓我們看一下真正work的示例。當輸入為6x6x32時，1x1卷積的形式是1x1x32，當只有一個1x1卷積核的時候，此時輸出為6x6x1。此時便可以體會到1x1卷積的實質作用：降維。當1x1卷積核的個數小於輸入channels數量時，即降維[3]。

注意，下圖中第二行左起第二幅影象中的黃色立方體即為1x1x32卷積核，而第二行左起第一幅影象中的黃色立方體即是要與1x1x32卷積核進行疊加運算的區域。

其實1x1卷積，可以看成一種全連線（full connection）。

第一層有6個神經元，分別是a1—a6，通過全連線之後變成5個，分別是b1—b5，第一層的六個神經元要和後面五個實現全連線，本圖中只畫了a1—a6連線到b1的示意，可以看到，在全連線層b1其實是前面6個神經元的加權和，權對應的就是w1—w6，到這裡就很清晰了：
第一層的6個神經元其實就相當於輸入特徵裡面那個通道數：6，而第二層的5個神經元相當於1*1卷積之後的新的特徵通道數：5。
w1—w6是一個卷積核的權係數，若要計算b2—b5，顯然還需要4個同樣尺寸的卷積核[4]。

上述列舉的全連線例子不是很嚴謹，因為影象的一層相比於神經元還是有區別的，影象是2D矩陣，而神經元就是一個數字，但是即便是一個2D矩陣（可以看成很多個神經元）的話也還是隻需要一個引數（1*1的核），這就是因為引數的權值共享。

注：1x1卷積一般只改變輸出通道數（channels），而不改變輸出的寬度和高度

1x1卷積核作用

• 降維/升維

由於 1×1 並不會改變 height 和 width，改變通道的第一個最直觀的結果，就是可以將原本的資料量進行增加或者減少。這裡看其他文章或者部落格中都稱之為升維、降維。但我覺得維度並沒有改變，改變的只是 height × width × channels 中的 channels 這一個維度的大小而已[5]。

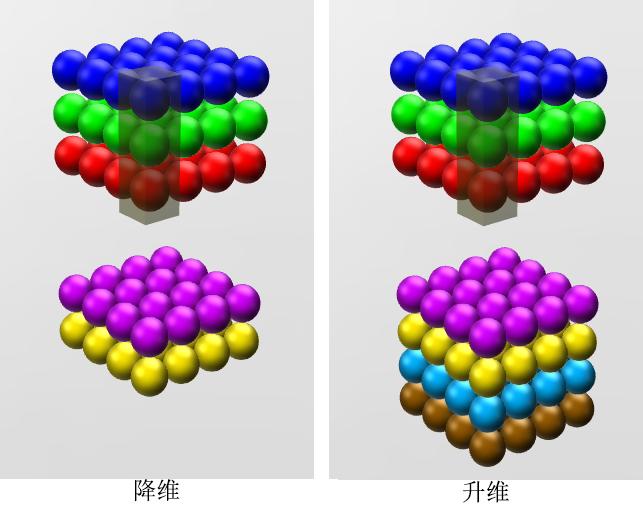
影象來自知乎ID: YJango[6]

• 增加非線性

1*1卷積核，可以在保持feature map尺度不變的（即不損失解析度）的前提下大幅增加非線性特性（利用後接的非線性啟用函式），把網路做的很deep。

備註：一個filter對應卷積後得到一個feature map，不同的filter(不同的weight和bias)，卷積以後得到不同的feature map，提取不同的特徵，得到對應的specialized neuron[7]。

• 跨通道資訊互動（channal 的變換）

例子：使用1x1卷積核，實現降維和升維的操作其實就是channel間資訊的線性組合變化，3x3，64channels的卷積核後面新增一個1x1，28channels的卷積核，就變成了3x3，28channels的卷積核，原來的64個channels就可以理解為跨通道線性組合變成了28channels，這就是通道間的資訊互動[7]。

注意：只是在channel維度上做線性組合，W和H上是共享權值的sliding window

1x1卷積核應用

Inception

1. 這一點孫琳鈞童鞋講的很清楚。1×1的卷積層（可能）引起人們的重視是在NIN的結構中，論文中林敏師兄的想法是利用MLP代替傳統的線性卷積核，從而提高網路的表達能力。文中同時利用了跨通道pooling的角度解釋，認為文中提出的MLP其實等價於在傳統卷積核後面接cccp層，從而實現多個feature map的線性組合，實現跨通道的資訊整合。而cccp層是等價於1×1卷積的，因此細看NIN的caffe實現，就是在每個傳統卷積層後面接了兩個cccp層（其實就是接了兩個1×1的卷積層）。

2. 進行降維和升維引起人們重視的（可能）是在GoogLeNet裡。對於每一個Inception模組（如下圖），原始模組是左圖，右圖中是加入了1×1卷積進行降維的。雖然左圖的卷積核都比較小，但是當輸入和輸出的通道數很大時，乘起來也會使得卷積核引數變的很大，而右圖加入1×1卷積後可以降低輸入的通道數，卷積核引數、運算複雜度也就跟著降下來了。

以GoogLeNet的3a模組為例，輸入的feature map是28×28×192，3a模組中1×1卷積通道為64，3×3卷積通道為128,5×5卷積通道為32，如果是左圖結構，那麼卷積核引數為1×1×192×64+3×3×192×128+5×5×192×32，而右圖對3×3和5×5卷積層前分別加入了通道數為96和16的1×1卷積層，這樣卷積核引數就變成了1×1×192×64+（1×1×192×96+3×3×96×128）+（1×1×192×16+5×5×16×32），引數大約減少到原來的三分之一。

同時在並行pooling層後面加入1×1卷積層後也可以降低輸出的feature map數量，左圖pooling後feature map是不變的，再加捲積層得到的feature map，會使輸出的feature map擴大到416，如果每個模組都這樣，網路的輸出會越來越大。

而右圖在pooling後面加了通道為32的1×1卷積，使得輸出的feature map數降到了256。GoogLeNet利用1×1的卷積降維後，得到了更為緊湊的網路結構，雖然總共有22層，但是引數數量卻只是8層的AlexNet的十二分之一（當然也有很大一部分原因是去掉了全連線層）[8]。

ResNet

ResNet同樣也利用了1×1卷積，並且是在3×3卷積層的前後都使用了，不僅進行了降維，還進行了升維，使得卷積層的輸入和輸出的通道數都減小，引數數量進一步減少，如下圖的結構[8]。

參考