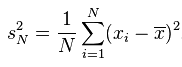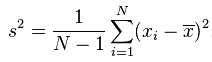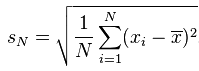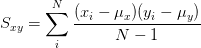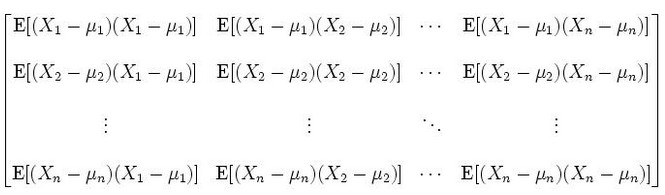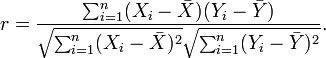演算法--偏差,方差,標準差,協方差,相關係數及相關理解
阿新 • • 發佈:2019-01-11
1 偏差與方差
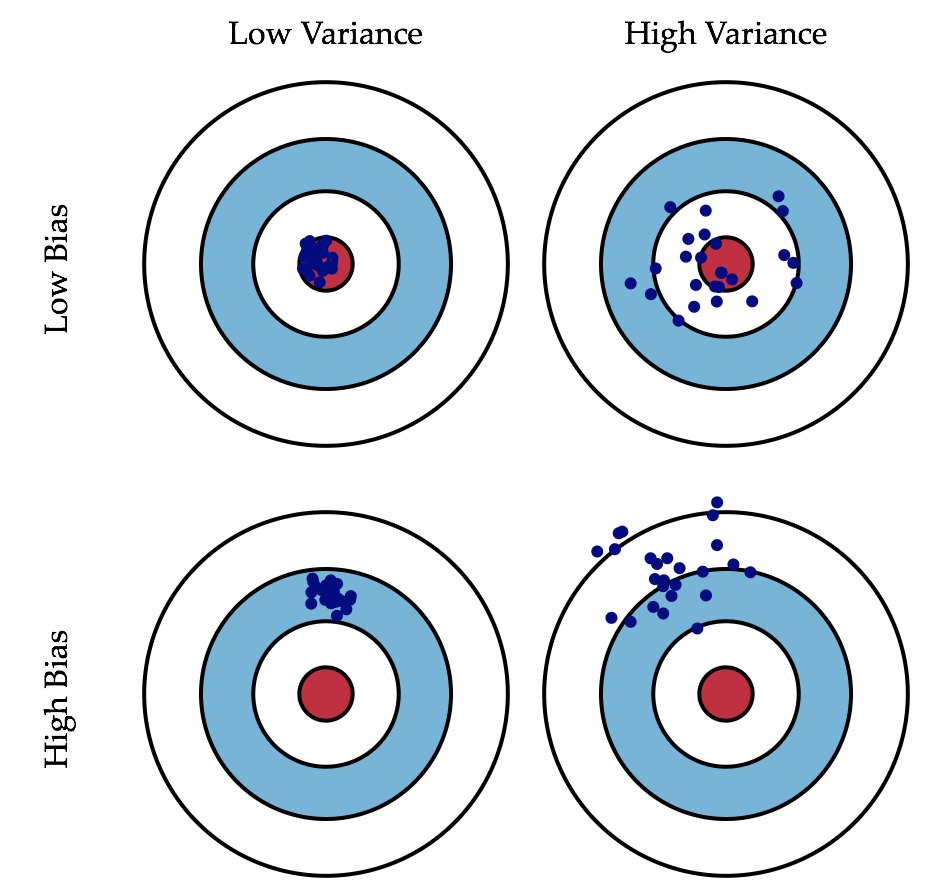
- 偏差(bias):描述的是預測值(估計值)的期望與真實值之間的差距。偏差越大,越偏離真實資料,如下圖第二行所示。
- 方差(variance):描述的是預測值的變化範圍,離散程度,也就是離其期望值的距離。方差越大,資料的分佈越分散,如下圖右列所示。
- 方差公式
Var(x)
=E((x−E(x))2)
=E(x2−2xE(x)+(E(x))2)
=E(x2)−2E(x)E(x)+(E(x))2
=E(x2)−2(E(x))2+(E(x))2
=E(x2)−(E(x))2
其實兩個公式是等價的 樣本方差公式:
式中:是樣本的均值
標準差(就是方差的平方根)
標準差公式:
樣本標準差公式:
為什麼使用標準差?
與方差相比,使用標準差來表示資料點的離散程度有3個好處:- 表示離散程度的數字與樣本資料點的數量級一致,更適合對資料樣本形成感性認知。依然以上述10個點的CPU使用率資料為例,其方差約為41,而標準差則為6.4;兩者相比較,標準差更適合人理解。
- 表示離散程度的數字單位與樣本資料的單位一致,更方便做後續的分析運算。
- 在樣本資料大致符合正態分佈的情況下,標準差具有方便估算的特性:66.7%的資料點落在平均值前後1個標準差的範圍內、95%的資料點落在平均值前後2個標準差的範圍內,而99%的資料點將會落在平均值前後3個標準差的範圍內。
2 協方差和相關係數
2 協方差covariance
定義
兩個隨機變數的協方差被定義為:
Cov(x,y)=E( (x−E(x)) (y−E(y)) )
Cov(x,y)=E( (x−E(x)) (y−E(y)) )
因此方差是一種特殊的協方差。當x=y時:Cov(x,y)=Var(x)=Var(y)。- 直觀理解
協方差表示的是兩個變數總體誤差的方差,這與只表示一個變數誤差的方差不同。 如果兩個變數的變化趨勢一致,也就是說如果其中一個大於自身的期望值,另外一個也大於自身的期望值,那麼兩個變數之間的協方差就是正值。 如果兩個變數的變化趨勢相反,即其中一個大於自身的期望值,另外一個卻小於自身的期望值,那麼兩個變數之間的協方差就是負值。 - 協方差矩陣(必定是一個方陣)
2 相關係數
- 相關係數通過方差和協方差定義。兩個隨機變數的相關係數被定義為:
性質
- 1、有界性
相關係數的取值範圍為-1到1,其可以看成是無量綱的協方差。 - 2、統計意義
值越接近1,說明兩個變數正相關性(線性)越強,越接近-1,說明負相關性越強,當為0時表示兩個變數沒有相關性。
- 1、有界性
- 相關係數通過方差和協方差定義。兩個隨機變數的相關係數被定義為: