1.最小二乘法

這是一個最簡單的凸優化問題，也是機器學習中的線性迴歸問題。最小二乘法問題是找到一個x∈Rn使得||Ax−b||2最小，其中A∈Rm×n是滿秩矩陣。最小二乘解為x=(ATA)−1ATb。普通的Matlab程式碼求解問題如下：

m = 16;n = 8;
A = randn(m,n);
b = randn(m,1);
x_ls = A \ b;

計算結果如下：

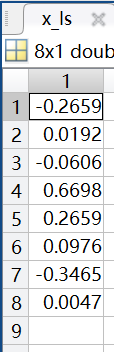
如果使用CVX工具包，同樣的問題求解如下：

m = 16;n = 8;
A = randn(m,n);
b = randn(m,1);
cvx_begin
    variable x(n)
    minimize( norm(A*x - b) )
cvx_end
 

可見，使用CVX的程式碼更加符合人類語言的閱讀習慣。

• cvx_begin是建立一個新的凸優化問題的命令，在它之後就可以寫出待求解的凸優化問題；
• variable x(n)定義了一個n維的變數；
• minimize( norm(A*x - b) )就是優化目標函式；
• cvx_end表示問題描述結束。

計算結果如下：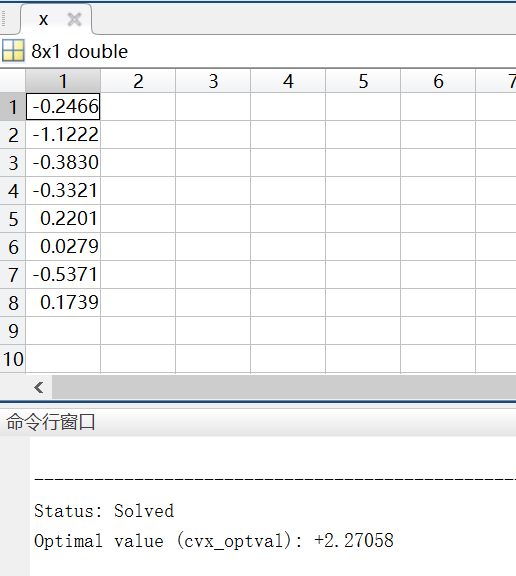
命令列視窗還會給出計算結果狀態和最優值。非常人性化。

2.有約束條件的最小二乘法

假如我們希望為最小二乘問題加上上界和下界約束，問題變成：
minimize ||Ax−b||
subject to l≤x≤u
上述的l和u是給定的與x具有相同維度的向量，不等式應為廣義不等式。Matlab呼叫二次規劃的函式求解如下：

m = 16;n = 8;
A = randn(m,n);
b = randn(m,1);
bnds = randn(n,2);
l = min(bnds, [], 2);
u = max(bnds, [], 2);
x_qb = quadprog(2*A'*A, -2*A'*b, [], [], [], [], l, u);

計算結果如下：

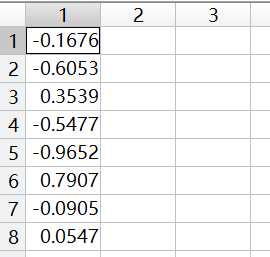
使用CVX後，程式碼如下：

m = 16;n = 8;
A = randn(m,n);
b = randn(m,1);
bnds = randn(n,2);
l = min(bnds, [], 2);
u = max(bnds, [], 2);
cvx_begin
    variable x(n)
    minimize(norm(A*x - b))
    subject to
        l <= x <= u
cvx_end
 

在任何計算機程式語言中不等式都不能連著寫的吧？CVX的設計應該是為了大大方便程式設計白痴的數學家編寫程式碼（哈哈哈~）。計算結果如下：

3.最優權衡曲線

這裡將顯示Matlab程式碼和CVX程式碼是可以混著用的。我們給目標函式加上懲罰因子λ，優化問題變為minimize ||Ax−b||+γ||x||1。其中γ是按照對數等分的行向量。γ的作用是權衡原目標函式和懲罰項。下面我們作出一條最優權衡曲線，曲線由以下程式繪出：

gamma = logspace(-2,2,20);
l2norm = zeros(size(gamma));
l1norm = zeros(size(gamma));
fprintf(1,'   gamma    norm(x,1)    norm(A*x-b)\n');
fprintf(1,'------------------------------------\n');
for k = 1:length(gamma)
    fprintf(1, '%8.4e', gamma(k));
    cvx_begin
        variable x(n)
        minimize(norm(A*x-b) + gamma(k)*norm(x,1));
    cvx_end
    l1norm(k) = norm(x,1);
    l2norm(k) = norm(A*x - b);
    fprintf(1, '    %8.4e    %8.4e\n', l1norm(k), l2norm(k));
end
plot(l1norm, l2norm);
xlabel('norm(x,1)');
ylabel('norm(A*x - b)');
grid on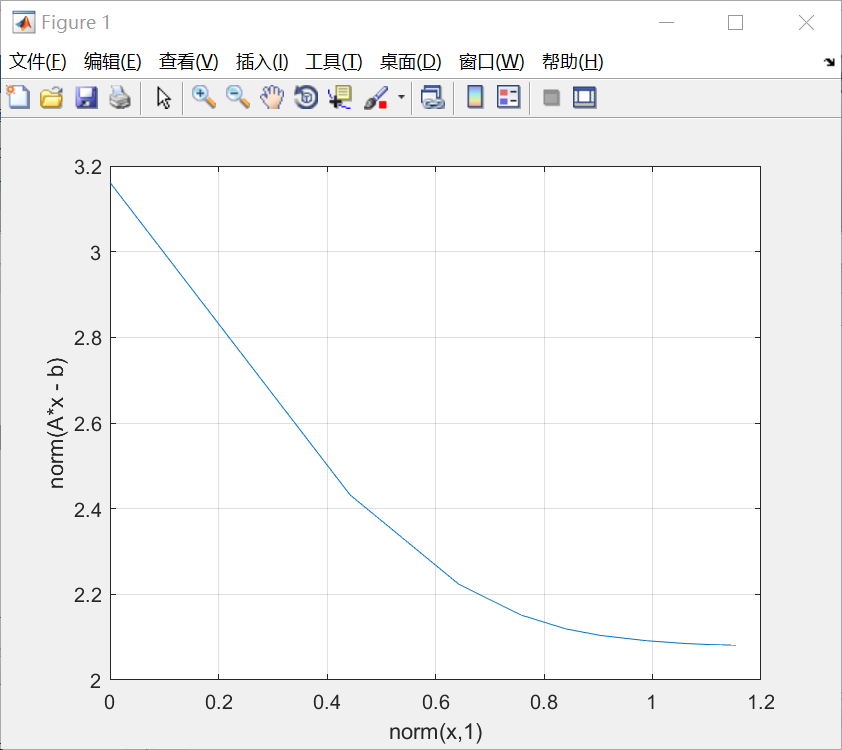

可見，當曲線收斂時，||Ax−b||2和||x||1得到了最優權衡。

以上就是CVX的快速入門。利用好這個工具將對凸優化的學習有很大的幫助！