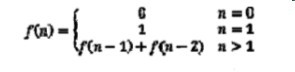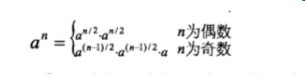斐波那契數列介紹：

常見的遞迴解法：

int Fibonacci(int n){
    if(n <= 0){
        return 0;
    }
    if(n == 1){
        return 1;
    }
    return Fibonacci(n-1)+Fibonacci(n-2);
}

遞迴解法的效率分析：

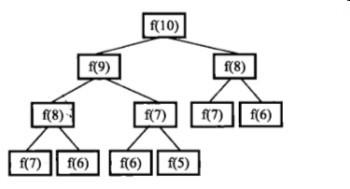
這棵樹是呼叫樹，有好多節點是重複的。隨著n的增大，重複的節點數目急劇增大。時間複雜度隨著n是指數增加的。

迴圈的效率更高的改進方法：

int Fibonacci(int n){
    if(n <= 0
 
){
        return 0;
    }
    if(n == 1){
        return 1;
    }
    int prev = 1;
    int next = 0;
    int all = 0;
    for(int i = 2;i <= n;++i){
        all = prev + next;
        next = prev;
        prev = all;
    }
    return all;
}

上述解法的時間複雜度為o（n）

時間複雜度為o（lgn）的解法：

數學先驗知識：

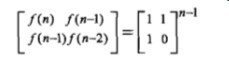
上面的公式可以用數學歸納發求得,轉化為求矩陣的乘積。
時間複雜度仍然為o（n）。

乘方的優化演算法，降低到O（lgn）

斐波那契的變形問題：

變形一（青蛙跳面試題，leetcode上面有）：

一隻青蛙一次跳一級或者2級臺階，求青蛙條n級臺階的方法數目？

思路：

s(n) = s(n-1)+s(n-2)，本質是斐波那契數列問題

進一步擴充套件：

青蛙，一次可以條1,2到n級臺階，那麼跳上n級臺階，方法數目？

思路：

f（n） = 2^(n-1);
可以用數學歸納法證明

斐波那契變形二：（方塊面試題）

把一個2*1的方塊，放進8個2*1的方塊，一共有多少種方法？

思路分析：

最後一塊豎著放，還需要f（7），橫著放的話，是f（6），
f（8） = f（7）+f（6）；

總結：

斐波那契問題靈活應用是解題關鍵