【劍指offer】面試題32:從上到下列印二叉樹
題目1:不分行從上到下列印二叉樹。從上往下打印出二叉樹的每個節點,同一層的節點從左到右的順序列印。
牛客網連結:https://www.nowcoder.com/questionTerminal/7fe2212963db4790b57431d9ed259701
例如輸入下圖的二叉樹,則依次打印出:8,6,10,5,7,9,11。
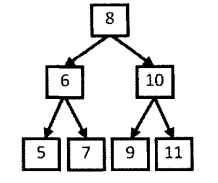
這道題實質上考察的就是樹的遍歷演算法,只是這種遍歷不是我們熟悉的前序、中序或者後序遍歷。由於我們不太熟悉這種按層遍歷的方法,可能一下子也想不清楚遍歷的過程。
因為按層列印的順序決定應該先列印的根節點,所以我們從樹的根節點開始分析。為了接下來能夠列印8的結點的兩個子節點,我們應該在遍歷到該結點時把值為6和10的兩個結點儲存到一個容器中,現在容器內就有兩個結點了。按照從左到右列印的要求,我們先取出值為6的結點。打印出6後把它的值分別為5和7的兩個結點放入資料容器。此時資料容器中有3個結點,值分別為10,5,7。接下來我們從資料容器中取出值為10的結點。注意到值為10的結點比值為5、7的結點先放入容器,此時又比這兩個結點先取出,這就是我們通常說的**先入先出**,因此不難看出這個容器應該是一個**佇列**。由於值為5,7,9,11的結點都沒有子節點,因此只要依次列印即可。
通過分析具體例子,我們可以找到從上到下列印二叉樹的規律:每次列印一個結點的時候,如果該節點有子節點,把該節點的子節點放到一個佇列的末尾。接下來到佇列的頭部取出最早進入佇列的節點,重複前面列印操作,直到佇列中所有的節點都被打印出來。
程式碼實現:
package com.zju.offer.tree; import java.util.ArrayList; /** * 不分行從上到下列印二叉樹 * 從上往下打印出二叉樹的每個節點,同一層的節點從左到右的順序列印 */ public class PrintFromTopToBottom { public class TreeNode { int val = 0; TreeNode left = null; TreeNode right = null; public TreeNode(int val) { this.val = val; } } public ArrayList<Integer> printFromTopToBottom(TreeNode root){ ArrayList<Integer> list = new ArrayList<>(); // 模擬一個佇列,也可以用LinkedList ArrayList<TreeNode> queue = new ArrayList<>(); if(root == null){ return list; } queue.add(root); while(queue.size() != 0){ // 將queue中第一個元素移除 TreeNode temp = queue.remove(0); // 如果將要移除的節點有左子節點,則加入queue if(temp.left != null){ queue.add(temp.left); } // 如果將要移除的節點有右子節點,則加入queue if(temp.right != null){ queue.add(temp.right); } // 將temp的值加入list中 list.add(temp.val); } return list; } }
本題實現程式碼中用的是一個ArrayList集合去模擬的佇列,每次移除下標為0的元素即為佇列的頭元素,也符合佇列“先進先出的特點”。

本題擴充套件:如何廣度優先遍歷一幅有向圖?同樣也可以基於佇列實現。樹是圖的一種特殊退化形式,從上到下按層遍歷二叉樹,從本質上來說就是廣度優先遍歷二叉樹。
舉一反三:不管是廣度優先遍歷一幅有向圖還是一棵樹,都要用到佇列。首先把起始節點(對樹而言是根節點)放入佇列。接下來每次從佇列的頭部取出一個節點,遍歷這個節點之後把它能到達的節點(對樹而言是子節點)都依次放入到佇列。重複這個遍歷過程,直到佇列中的節點全部被遍歷為止。
題目2:分行從上到下列印二叉樹。從上到下按層列印二叉樹,同一層的節點按從左到右的順序列印,每一層列印到一行。
如下案例所示:

列印結果為:
8
6 10
5 7 9 11
這道題和前面的題類似,也可以用一個佇列來儲存將要列印的節點。為了把二叉樹的每一行單獨列印到一行裡,我們需要兩個變數:一個變量表示在當前層中還沒有列印的節點數;另外一個變量表示下一層節點的數目。
public class PrintFromTopToBottom {
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
public ArrayList<Integer> printFromTopToBottom_Method1(TreeNode root){
ArrayList<Integer> list = new ArrayList<>();
// 模擬一個佇列,也可以用LinkedList
ArrayList<TreeNode> queue = new ArrayList<>();
if(root == null){
return list;
}
queue.add(root);
int nextLevel = 0;
int toBePrinted = 1;
while(queue.size() != 0){
// 將queue中第一個元素移除
TreeNode temp = queue.remove(0);
// 如果將要移除的節點有左子節點,則加入queue
if(temp.left != null){
queue.add(temp.left);
nextLevel++;
}
// 如果將要移除的節點有右子節點,則加入queue
if(temp.right != null){
queue.add(temp.right);
nextLevel++;
}
// 將temp的值加入list中
list.add(temp.val);
System.out.print(temp.val + " ");
--toBePrinted;
if(toBePrinted == 0){
System.out.println();
toBePrinted = nextLevel;
nextLevel = 0;
}
}
return list;
}
// 測試
public static void main(String[] args) {
PrintFromTopToBottom p = new PrintFromTopToBottom();
TreeNode root = p.new TreeNode(8);
TreeNode node1 = p.new TreeNode(6);
TreeNode node2 = p.new TreeNode(10);
TreeNode node3 = p.new TreeNode(5);
TreeNode node4 = p.new TreeNode(7);
TreeNode node5 = p.new TreeNode(9);
TreeNode node6 = p.new TreeNode(11);
root.left = node1;
root.right = node2;
node1.left = node3;
node1.right = node4;
node2.left = node5;
node2.right = node6;
p.printFromTopToBottom_Method1(root);
}
}
變數 toBePrinted 表示在當前層中還沒有列印的節點數,而變數 nextLevel 表示下一層的節點數。如果一個節點有子節點,則每把一個子節點加入佇列,同時把變數 nextLevel 加1。每列印一個節點,toBePrinted 減 1。當 toBePrinted 變成 0 時,表示當前層的所有節點已經列印完畢,可以繼續列印下一層。
題目3:之字形列印二叉樹。
請實現一個函式按照之字形列印二叉樹,即第一行按照從左到右的順序列印,第二層按照從右至左的順序列印,第三行按照從左到右的順序列印,其他行以此類推。
按之字形順序列印二叉樹需要兩個棧。我們在列印某一層的節點時,把下一層的子節點儲存到相應的棧裡。如果當前列印的是奇數層(第一層、第三層等),則先儲存左子節點再儲存右子節點到第一個棧裡(因為棧的後進先出特點);如果當前列印的是偶數層(第二層、第四層等),則先儲存右子節點再儲存左子節點到第二個棧裡。接下來逐個把位於棧頂的節點彈出棧並列印即可。
使用巢狀集合型別來儲存 stack1 和 stack2 中彈出的資料,每一個內層小集合中儲存一層的資料。
package com.zju.offer.tree;
import java.util.ArrayList;
import java.util.Stack;
public class PrintFromTopToBottom {
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
/**
* 之字形列印:奇數從左往右列印、偶數從右往左列印
*/
public ArrayList<ArrayList<Integer>> Print(TreeNode root){
// 層數索引
int layer = 1;
// stack1 儲存奇數層節點
Stack<TreeNode> stack1 = new Stack<TreeNode>();
stack1.push(root); // 因為根節點是奇數層,所以將根節點先儲存到stack1中
// stack2 儲存偶數層節點
Stack<TreeNode> stack2 = new Stack<TreeNode>();
// 採用雙層集合,每一個內層集合儲存一層資料
ArrayList<ArrayList<Integer>> list = new ArrayList<ArrayList<Integer>>();
while(!stack1.empty() || !stack2.empty()){
if(layer % 2 != 0){
// 列印奇數層
ArrayList<Integer> temp = new ArrayList<Integer>();
while(!stack1.empty()){
TreeNode node = stack1.pop();
if(node != null){
temp.add(node.val);
System.out.print(node.val + " ");
// 由於當前層是奇數層,所以它的下一層是要從右往左列印
// 因此按照棧的"後進先出"的特性,先儲存左子節點,再儲存右子節點
stack2.push(node.left);
stack2.push(node.right);
}
}
if(!temp.isEmpty()){
list.add(temp);
layer++;
System.out.println();
}
}else{
// 列印偶數層
ArrayList<Integer> temp = new ArrayList<Integer>();
while(!stack2.isEmpty()){
TreeNode node = stack2.pop();
if(node != null){
temp.add(node.val);
System.out.print(node.val + " ");
// 由於當前層是偶數層,所以它的下一層是要從左往右列印
// 因此按照棧的"後進先出"的特性,先儲存右子節點,再儲存左子節點
stack1.push(node.right);
stack1.push(node.left);
}
}
if(!temp.isEmpty()){
list.add(temp);
layer++;
System.out.println();
}
}
}
return list;
}
// 測試
public static void main(String[] args) {
PrintFromTopToBottom p = new PrintFromTopToBottom();
TreeNode root = p.new TreeNode(8);
TreeNode node1 = p.new TreeNode(6);
TreeNode node2 = p.new TreeNode(10);
TreeNode node3 = p.new TreeNode(5);
TreeNode node4 = p.new TreeNode(7);
TreeNode node5 = p.new TreeNode(9);
TreeNode node6 = p.new TreeNode(11);
root.left = node1;
root.right = node2;
node1.left = node3;
node1.right = node4;
node2.left = node5;
node2.right = node6;
p.Print(root);
}
}
